4.1.2. Метод деления отрезка пополам

 

Метод деления отрезка пополам является простейшим последовательным  методом минимизации. Он позволяет для любой функции f(x)Q[a, b] построить последовательность вложенных отрезков      [a, b]  [a₁,b₁]  …  [a_n-1, b_n-1]  [a_n, b_n],  каждый из которых содержит хотя бы одну из точек оптимума х* функции  f(x).

М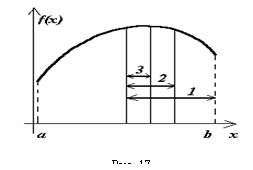 етод основан на делении текущего отрезка [а, b], где содер­жится искомый экстремум, на две равные части с последующим выбором одной из половин, в которой локализуется максимум в качестве следующего текущего отрезка. Экстремум локализуется путем сравнения двух значений критерия оптимальности в точ­ках, отстоящих от середины отрезка на  /2, где  — погрешность решения задачи оптимизации.

Если f(х +  /2) > f(х -  /2), то максимум располагается на пра­вой половине текущего отрезка [а, b] , в противном случае — на левой.

Процесс поиска завершается при достижении отрезком [а, b]  величины заданной погрешности  .

К недостаткам метода относится его работоспособность толь­ко для одноэкстремальных функций f(х) (т.е. таких, которые со­держат один экстремум того типа, который мы ищем в задаче), так как в других случаях при сравнении двух критериев в сосед­них точках невозможно правильно выбрать следующий интервал, где находится максимум.

На рис. 17 приведены три этапа метода половинного деле­ния. Сплошными вертикальны­ми линиями отмечены середины отрезков, а пунктирными — вы­числяемые значения критерия оптимальности слева и справа на  /2 от середин.

Иллюстрация метода заключается в следующем: 1 – интервал, включающий в себя искомый максимум функции после первого этапа (первого деления пополам); 2, 3 – то же соответственно после второго и третьего этапов.

Существует и другой вари­ант алгоритма, заключающийся в следующем. После нахожде­ния середины отрезка (напри­мер, точка с₁) в одной из полови­нок (допустим, в левой) находят среднюю точку (точка с₂) и, срав­нивая значения функции в этих точках, определяют, в какой из половинок находится экстремум. Если f(c₁)<f(c₂), то в качестве следующего отрезка выбираем отрезок [а, с₁], если же f(c₁)>f(c₂), то берут новую точку в середине правой половины (точка с₃) и в ней вычисляют функцию. В зависимости от сравнения зна­чений функции в точках с₃ и с₁ выбирают новый отрезок [с₁, b] или [с₂, с₃] и т.д.

Второй вариант метода не имеет с точки зрения эффективно­сти принципиального отличия от первого, так как эффективность принято оценивать по наихудшему варианту (т.е. по двум вычис­лениям f(x) на каждом шаге). В первом варианте метода есть одна особенность, которая его делает очень эффективным при экспериментальном отыскании экстремума (например, при авто­матической настройке технических систем или при практическом поиске наилучших условий деятельности экономического объек­та). Малые отклонения от текущей точки обеспечивают в процес­се поиска отсутствие "шараханий", сопровождающихся резкими отклонениями состояния системы.

Пример 14. Найти минимальное значение f* и точку минимума х* функции

f(x)=x⁴+8x³-6x²-72х на отрезке [1.5; 2]. Точку х* найти с погрешностью =0,05.

Решение. 1 способ. Вычисления представим в виде табл. 6.

                                                                                                                                                       Таблица 6

n	an	bn	f(an)	f(bn)	cn	f(cn)	|an-bn|
0	1,500	2,000	-89,438	-88,000	1,750	-92,121	0,500
1	1,500	1,750	-89,438	-92,121	1,625	-91,543	0,250
2	1,625	1,750	-91,543	-92,121	1,688	-92,033	0,125
3	1,688	1,750	-92,033	-92,121	1,719	-92,129	0,063
4	1,719	1,750	-92,129	-92,121	1,734	-92,138	0,031

В итоге получили:  х*  1.734  и  f*  f (1.734) = - 92.138.

В таблице a_n и b_n являются концами отрезков, а с_n – середина соответствующего отрезка, то есть 

Полагая , находим  х* с абсолютной погрешностью, не превосходящей величины

                                                    (**)

Используя условие _n   , из последнего выражения можно найти необходимое число шагов n для обеспечения требуемой точности . Однако на практике часто поступают иначе: определив границы отрезка  [a_n; b_n], вычисляют _n по формуле (**)  и сравнивают с заданной точностью .

В нашем случае положим  =0,02 < 2=0,1.  Построим последовательность вложенных отрезков [a_n; b_n] по рекуррентным формулам, записывая результаты вычислений в табл. 7:

Таблица 7

n	an	bn		х1(n)	х2(n)	f(x1(n))	f(x2(n))	Примечания
0	1.5	2	0.25	1.74	1.76	-92.135	-92.096
1	1.5	1.76	0.13	1.62	1.64	-91.486	-91.696
2	1.62	1.76	0.07	1.68	1.70	-91.995	-92.084
3	1.68	1.76	0.04					точность достигнута

 

Следовательно, х*  1,72, и  f*  f (1.72) = - 92.13.

Пример 15. Методом деления отрезка пополам найти точку минимума х* функции

 на отрезке [0.5; 1] с точностью =0,05.

Решение. Сначала произведем вычисления, используя первый способ.

                                                                                                               Таблица 8

 

n	an	bn	f(an)	f(bn)	cn	f(cn)	|an-bn|
0	0,5	1	-3,591	-0,5	0,75	-2,439	0,5
1	0,5	0,75	-3,591	-2,439	0,625	-3,133	0,25
2	0,5	0,625	-3,591	-3,133	0,563	-3,395	0,125
3	0,5	0,563	-3,591	-3,395	0,531	-3,501	0,063
4	0,5	0,531	-3,591	-3,501	0,516	-3,548	0,031

 

Получаем, х* 0,516, и  f*  f (0,516) = -3,548.

 

Решим этот же пример вторым способом. Для этого составим табл. 9:

Таблица 9

 

n	an	bn		х1(n)	х2(n)	f(x1(n))	f(x2(n))	Примечания
0	0,5	1	0,25	0,74	0,76	-2,502	-2,374
1	0,5	0,74	0,12	0,61	0,63	-3,201	-3,109
2	0,5	0,63	0,065	0,555	0,575	-3,422	-3,448
3	0,5	0,575	0,0375					точность достигнута

 

Следовательно, х* 0,5375, и  f*  f (0,5375) = -3,4814.

Пример 16. Дана функция f(x) = sin (x+1). Найти максимум на интервале [-1; 2] с точностью =0,05.

Решение. Вычисления представим в виде табл. 10.

                                                                                                                                                    Таблица 10

n	an	bn	f(an)	f(bn)	cn	f(cn)	|an-bn|
0	-1	2	0	0,1411	0,5	0,9975	3
1	0,5	2	0,9975	0,1411	1,25	0,7781	1,5
2	0,5	1,25	0,9975	0,7781	0,875	0,9541	0,75
3	0,5	0,875	0,9975	0,9541	0,6875	0,9932	0,375
4	0,5	0,6875	0,9975	0,9932	0,5938	0,9997	0,1875
5	0,5	0,5938	0,9975	0,9997	0,5469	0,9997	0,0938
6	0,5469	0,5938	0,9997	0,9997	0,5703	1	0,0469

 

Итак,

Решим этот же пример вторым способом. Для этого составим табл. 11:

                                                                                                                                                               Таблица 11

n	an	bn		х1(n)	х2(n)	f(x1(n))	f(x2(n))	Примечания
0	-1	2	1,5	0,55	0,45	0,9998	0,9927
1	0,55	2	0,725	1,325	1,225	0,7288	0,7935
2	0,55	1,225	0,3375	0,9375	0,8375	0,9335	0,9646
3	0,55	0,8375	0,1438	0,7438	0,6438	0,9851	0,9997
4	0,55	0,6438	0,0469					точность достигнута

 

Следовательно, х*  0,5969, f*  0.9997.