8. Приклади реалізації оптимізаційних задач
Задача №1
Підприємство виробляє два види продукції. Для виготовлення першого виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
Вихідний ресурс |
Витрати вихідного ресурсу на одиницю продукції, грн. |
Запаси, грн. |
|
І вид |
ІІ вид |
||
Сировина |
0,8 |
0,5 |
400 |
Електроенергія |
0,4 |
0,8 |
365 |
Вивчення ринку збуту показало, що місячний попит на І вид продукції перевищує попит на ІІ вид не більше ніж на 100 кг. Окрім того, встановлено, що попит на І вид продукції не перевищує 350 кг за місяць. Роздрібна ціна одиниці продукції І виду - 16 грн., а ІІ – 14 грн.
Яку
кількість кожного виду продукції
повинно щомісяця виробляти підприємство,
щоб виручка
від реалізації продукції була максимальною?
Розв’яжемо задачу за допомогою графічного методу
Позначимо:
через
- місячний обсяг випуску продукції І
виду, кг; через
- місячний обсяг випуску продукції ІІ
виду, кг.
Складемо економіко-математичну модель задачі.
За критерій оцінки приймемо виручку від реалізації продукції (В), яка визначається за формулою
,
де
- ціна одиниці і-го
виду продукції, грн.;
-
обсяги
виробленої продукції, кг.
Цільова функція буде мати вигляд
при обмеженнях
Знайдемо область припустимих розв’язків.
1.
,
2.
,
3.
,
4.
4.
- І чверть.
Областю
припустимих розв’язків є п’ятикутник
.
Для
знаходження екстремальних значень
цільової функції при графічному розв’язку
знайдемо вектор
,
який є градієнтом функції
.
Проводимо
лінію рівня
,
яка є перпендикулярною до вектора
.
Оскільки цільова функція досліджується
на максимум, то переміщується лінія
рівня за напрямком вектора
.
Точкою виходу з області припустимих
значень є точка
,
координати якої визначаються як перетин
прямих
та
.
Розв’язком системи є значення
кг
і
кг.
Таким чином, найбільше значення функції або максимальна виручка від реалізації продукції складе
Задача №2
Підприємство виробляє три види продукції. Для виготовлення кожного виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
Вихідний ресурс |
Витрати вихідного ресурсу на одиницю продукції, тис. грн. |
Запаси, тис. грн. |
||
|
І вид |
ІІ вид |
ІІІ вид |
|
Сировина |
2 |
1 |
3 |
200 |
Електроенергія |
1 |
2 |
1 |
300 |
Роздрібна ціна одиниці продукції І виду - 3 тис. грн., ІІ виду – 4 тис. грн., ІІІ виду – 2 тис. грн.
Яку кількість кожного виду продукції повинно щомісяця виробляти підприємство, щоб виручка від реалізації продукції був максимальним?
Розв’яжемо задачу за допомогою симплексного методу
при обмеженнях
Переведемо економіко-математичну модель до канонічного вигляду
Складемо симплексну таблицю першого кроку
|
БЗ |
3 |
4 |
2 |
0 |
0 |
|
|
|
|
|
|
|||
0 |
|
2 |
1 |
3 |
1 |
0 |
200 |
0 |
|
1 |
2 |
1 |
0 |
1 |
300 |
|
-3 |
-4 |
-2 |
0 |
0 |
0 |
|
Заповнимо індексний рядок для змінних за формулами
і
для вільного члена
.
Оскільки,
маємо від’ємні
оцінки
при
умові, що цільова функція
,
то знайдений розв’язок не є оптимальним.
Складемо симплексну таблицю другого
кроку.
За ключовий стовпець
обираємо четвертий стовпець, який
відповідає найменшому значенню індексної
оцінки -4, а за індексний елемент 2, тому
що найменше значення відношення вільного
члена до відповідного елемента ключового
стовпця
.
|
БЗ |
3 |
4 |
2 |
0 |
0 |
|
|
|
|
|
|
|||
0 |
|
|
0 |
|
1 |
|
50 |
4 |
|
|
1 |
|
0 |
|
150 |
|
-1 |
0 |
0 |
0 |
2 |
600 |
|
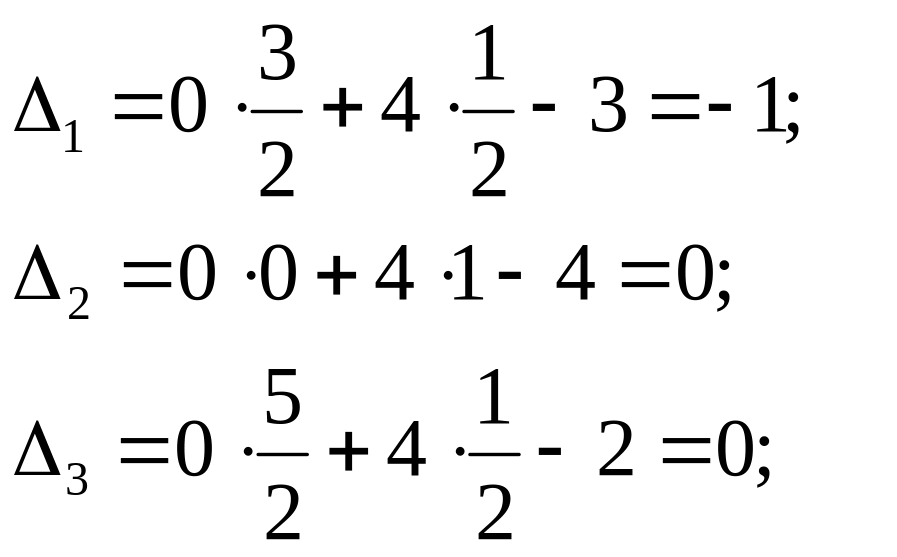
Оскільки, маємо від’ємну оцінку при умові, що цільова функція , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю третього кроку.
За
ключовий стовпець обираємо третій
стовпець, який відповідає від’ємному
значенню індексної оцінки -1, а за
індексний елемент
,
тому що найменше значення відношення
вільного члена до відповідного елемента
ключового стовпця
.
|
БЗ |
3 |
4 |
2 |
0 |
0 |
|
|
|
|
|
|
|||
3 |
|
1 |
0 |
|
|
|
|
4 |
|
0 |
1 |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
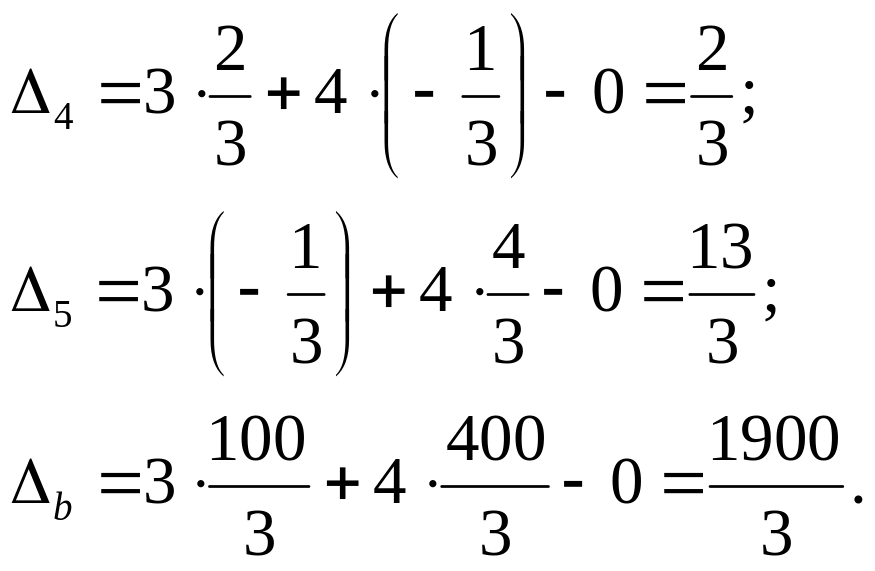
Оскільки,
всі оцінки
при
умові, що цільова функція
,
то знайдений розв’язок є оптимальним.
Таким чином, підприємству необхідно виробляти продукцію І і ІІ виду, а випуск продукції ІІІ виду припинити.
Задача №3
Гірничо-збагачувальний
комбінат виробляє товарну продукцію –
концентрат, який реалізує на внутрішній
і зовнішній ринки збуту. При продажу
тон концентрату на внутрішній ринок
витрати на реалізацію складають
грн., а при продажу
тон концентрату на зовнішній ринок -
грн.
Визначити, яку кількість концентрату (тон) необхідно продавати на внутрішній і зовнішній ринки, щоб витрати на реалізацію були мінімальними, якщо за рік реалізується 10000 тис. тон концентрату.
Розв’яжемо задачу за допомогою методу множників Лагранжа
Складемо економіко-математичну модель задачі. Цільова функція економіко-математичної моделі має вигляд
,
де - витрати на реалізацію концентрату, грн.
при обмеженнях
Складемо функцію Лагранжа
.
За
необхідною умовою існування екстремуму
функції, знайдемо частинні похідні
функції
за змінними
,
прирівняємо їх до нуля та одержимо
систему рівнянь
Після елементарних перетворень одержуємо
Звідки
тис. тон;
тис.
тон.
Перевіримо одержані значення на оптимальність. Використаємо достатню умову екстремуму функції двох змінних.
Одержуємо,
Звідси,
,
тому у точці (5000; 5000) існує екстремум
функції. При
одержуємо,
що у досліджуваній точці існує мінімум
функції, значить, мінімальні витрати
на реалізацію концентрату дорівнюють
грн.
Задача №4
Міністерство розглядає пропозицію щодо нарощення виробничих потужностей для збільшення випуску однорідної продукції на чотирьох підприємствах, що належать даній галузі.
Для розширення виробництва міністерство виділяє кошти у обсязі 120 млн. грн. з дискретністю 20 млн. грн. Приріст випуску продукції на підприємствах залежить від суми виділених коштів, значення якого представлені у таблиці.
Кошти, млн. грн. |
Приріст випуску продукції, млн. грн. |
|||
Підприємство №1 |
Підприємство №2 |
Підприємство №3 |
Підприємство №4 |
|
20 |
8 |
10 |
12 |
11 |
40 |
16 |
20 |
21 |
23 |
60 |
25 |
28 |
27 |
30 |
80 |
36 |
40 |
38 |
37 |
100 |
44 |
48 |
50 |
51 |
120 |
62 |
62 |
63 |
63 |
Знайти розподіл коштів між підприємствами, що забезпечує максимальний приріст випуску продукції, причому на одне підприємство може виділятися не більше однієї інвестиції.
Розв’яжемо задачу за допомогою методу динамічного програмування
Розіб’ємо розв’язок задачі на чотири етапи за кількістю підприємств, на які передбачається здійснити інвестиції.
Рекурентне співвідношення буде мати вигляд:
для підприємства №1
для всіх інших підприємств
.
Розв’язок будемо виконувати у відповідності до рекурентних співвідношень у чотири етапи.
1 етап.
Інвестиції надаємо тільки першому підприємству. Тоді:
2 етап.
Інвестиції виділяємо першому і другому підприємствам. Рекурентне співвідношення для другого етапу має вигляд
Тоді
при
3 етап.
Фінансуємо другий етап і третє підприємство. Розрахунки виконуємо за формулою
Тоді:
при
4 етап.
Інвестиції розміром 120 млн. грн. розподіляємо між третім етапом і четвертим підприємством
Одержано
умови управління від першого до
четвертого етапу. Повернемося від
четвертого до першого етапу. Максимальний
приріст випуску продукції у 64 млн. грн.
одержано на четвертому етапі як
,
тобто 23 млн. грн. відповідають виділенню
40 млн. грн. четвертому підприємству
(див. табл.). Відповідно до третього етапу
41 млн. грн. одержано як
,
тобто 21 млн. грн. відповідає виділенню
40 млн. грн. третьому підприємству.
Відповідно до другого етапу, 20 млн. грн.
одержано при виділенні 40 млн. грн. другому
підприємству.
Таким чином, інвестиції обсягом 120 млн. грн. доцільно виділяти другому, третьому і четвертому підприємствам по 40 млн. грн., при цьому максимальний приріст продукції складе 64 млн. грн.
Задача 5
Наведена таблиця міжгалузевих зв’язків для 3 галузей промисловості. Необхідно визначити обсяги випуску продукції кожної галузі, якщо кінцевий продукт буде змінюватися і дорівнювати відповідно 40, 30 і 50 млн. грн.
Галузь промисловості |
Обсяг продукції, млн. грн. |
Міжгалузеві потоки в галузях, млн. грн. |
||
№1 |
№2 |
№3 |
||
1 |
200 |
40 |
60 |
50 |
2 |
320 |
100 |
100 |
80 |
3 |
400 |
80 |
120 |
100 |
Для розв’язання застосуємо задачу про складання міжгалузевого балансу Леонтьєва
Складемо матрицю технології виробництва, використовуючи формулу
.
Знайдемо
матрицю
,
обернену до матриці (
),
визначник якої
.
Знайдемо алгебраїчні доповнення до елементів матриці ( ):
Тоді матриця коефіцієнтів сумісного споживання має вигляд
Обсяги продукції, які необхідно виробляти кожній галузі будуть дорівнювати
Таким чином, випуск продукції в першій галузі необхідно зменшити до 140,65 млн. грн., у другій – до 219,39 млн. грн., а у третій – до 251,36 млн. грн.