6. Методы устранения автокорреляции

1.Обобщенный МНК (ОМНК)

Рассмотрим исходную модель в моменты времени t и t–1: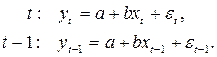 

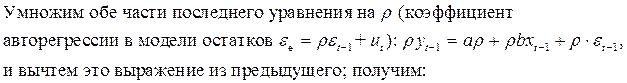
– есть случайная величина, так как  и  – случайные величины,

, так как  и  .

Остаток  не коррелирует ни с одним регрессором, следовательно, можно применить классический МНК. Оценка параметра b вычисляется непосредственно, а оценка параметра a вычисляется так:  .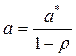

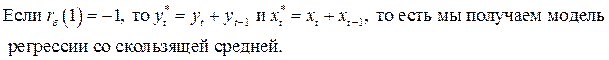
ОМНК может применяться для данных, начиная с момента  , т.е. первое наблюдение теряется; его можно восстановить для  и  , используя поправку Прайса–Уинстена:

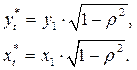
Если наше предположение о том, что остатки описанные  – моделью первого порядка соответствуют действительности, то можно показать, что  .

При большой протяженности временного ряда значения и  действительно оказываются близки друг к другу. В матричной форме отыскание столбца B с помощью ОМНК выражается так:

B = (X^TΩ_ρX)^-1X^TΩ_ρY, где

 

 

 

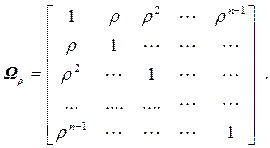
2. Метод Кохрана – Оркатта (итерационный)

Первая итерация: вначале по МНК оценивается регрессия  . Определяются столбец остатков  и столбец  . Далее оценивается авторегрессия остатков по схеме  :

, отсюда находится оценка  .

Вторая итерация: Введем новые переменные: w_t = y_t – ρy_t-1, z_t = x_t – ρx_t-1.

Построим регрессию  По ней определим (ε₁)_t и (ε₁)_t-1. Далее опять построим авторегрессию остатков  , отсюда находим оценкуρ₁.

Третья итерация: Опять введем новые переменные (w₁)_t = w_t – ρ₁w_t–1,

(z₁)_t = z_t – ρ₁z_t–1 и построим регрессию  По ней определим

остатки (ε₂)_t и (ε₂)_t-1. Построим авторегрессию остатков  и по ней найдем оценку ρ₂.

Итерационный процесс продолжается до тех пор, пока разность между предыдущей и последующей оценками ρ не станет по модулю меньше любого наперед заданного числа. После того, как определено значение ρ, строится регрессия по уже знакомой модели:

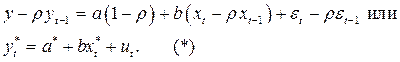
Применяя к этому уравнению классический МНК находим  и  , рассчитываем значение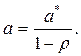 

3. Метод Хилдрета-Лу

Этот метод предполагает перебор значений  с достаточно малым шагом, например, 0,01 и подстановку его в уравнение (*). Та величина  , при которой стандартная ошибка регрессии в данной модели будет наименьшей, принимается в качестве наилучшей оценки