
- •Предприятию выдан заказ, в котором определены сроки, номенклатура и объем поставки:
- •Гипотезы экономического моделирования
- •Предприятию выдан заказ, в котором определены сроки, номенклатура и объем поставки:
- •Требуется определить оптимальную загрузку машин (программу производства) с использованием критерия – минимальные издержки производства
- •Решение задачи графо-аналитическим методом
- •Графический образ симплекса модели линейного программирования для распределения производственных мощностей
- •Конец Задания №2 Задание №3
- •Алгоритм и методы поиска решения
- •Задание №4
- •Конец Задания №4
- •Эволюционная оптимизация
- •Блок-схема генетического алгоритма (Дарвин алгоритм)
Эволюционная оптимизация
В алгоритмах эволюционной оптимизации используются идеи естественного процесса генезиса (естественного отбора). Используются формальные категории: популяция, индивид, особь, скрещивания, мутации и отбор по критерию.
Популяция - совокупность всех рассматриваемых возможных решений,
Особь (индивидуум) – одно из возможных решений, в т.ч. оптимальное,
Ген – переменная в возможном решении (в особи),
Аллель – генетический атом в гене (бит в переменной).
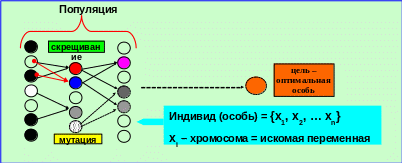
Популяция = совокупность возможных решений (индивидов, особей). Каждый индивид – совокупность генов, т.е. искомых переменных. Проводится математический генезис и отбор из большого числа особей по некоторому критерию, заданному пользователем. Новые (дочерние) особи наследуют некоторые признаки и свойства старых (родительских), причем каждый дочерний элемент может наследовать свойства и признаки разных родителей - это эффект скрещивания.

Хромосома (искомая переменная) – рассматривается как двоичное число. Скрещивание особей производится путем скрещивания их одноименных хромосом (одинаковые переменные в разнвх особях).
i-я хромосома k-ой особи = |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
i-я хромосома (k+1)-ой особи = |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Скрещивание особей производится путем скрещивания их одноименных хромосом (одинаковых переменных в скрещиваемых особях).
Процесс математического генезиса имеет свойство авторегулирования (сходимости), для этого в генерации дочерних особей участвуют те родители, свойства и признаки которых наиболее соответствуют целевому критерию.

Решение задач оптимизации с использованием эволюционных алгоритмов представляет собой реализацию метода стохастического градиентного спуска (Дарвин алгоритм), при котором исследование пространства возможных решений производится одновременно из множества исходных точек (индивидов популяции).
Блок-схема генетического алгоритма (Дарвин алгоритм)


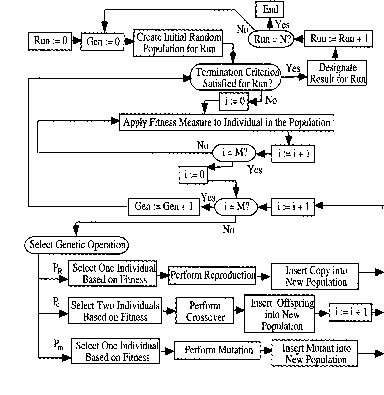
PR – параметр (вероятность) репродукции
Pc – параметр (вероятность) скрещивания
Pm – параметр (вероятность) мутации
x 21
(3)
(4)
F0
(x11=5; x21=1)
(6)
(5)
(
F→min
F→min x11
(1)
Решение задачи: minF = 211
x11=5; x21=1;
f3= а11x11 + а12x12 = N1; x12 = (1/а12)(N1(30) - а11x11) = 30/13 – (6/13)5 = 0;
f4= а21x21+а22x22 =N2; x22 = (1/а22)(N2(96) – а21x21) =96/13–(24/13)1 = 5,54
а22 = 13 а21= 24 72/13 = 5,54
