Конец Задания №2 Задание №3

Второй этап — определение и исследование математических задач, к которым приводит востребованная математическая модель, т.е. тех математических технологий, которые лягут в основу вычислительной (рекурсивной) схемы модели.

3 шаг. Третья Лингвистическая форма математической модели (на языке программирования для ЭВМ или на языке инструментальной системы (Excel), символьный формат, символьный формат, в символах языка инструментальной системы)

Используем современный индустриальный подход к проектированию математической модели. С этой целью используем аналитическую вычислительную среду прикладного инструментального пакета Excel

В операторных символах прикладного пакета Excel

Алгоритм и методы поиска решения

В процедуре поиска решения Microsoft Excel_2003 при решении задач математического программирования используется два вида численных алгоритмов: (1) сопряженных градиентов и (2) Ньютона

(1) Алгоритм нелинейной оптимизации Generalized Reduced Gradient (GRG2) – сопряженного градиента (для возможных направлений), разработанный в Cleveland State University).

(2) Алгоритмы симплексного метода и метода "branch-and-bound" – последовательного приближения Ньютона для решения линейных и целочисленных задач с ограничениями, разработанный в Frontline Systems, Inc.

Кроме того, используются:

(3) Алгоритмы эволюционного исчисления

Методы поиска решения Microsoft Excel_2010

В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.

1. Нелинейный метод обобщенного понижающего градиента (ОПГ) Используется для гладких нелинейных задач: все функции, которые используются для математического описания решаемой задачи дифференцируемы необходимое число раз.

2. Симплекс-метод Используется для линейных задач. (Рассмотрен выше)

3. Эволюционный метод Используется для негладких задач. (Рассмотрен ниже).

Модель распределения в процедуре поиска решения Microsoft Excel_2003

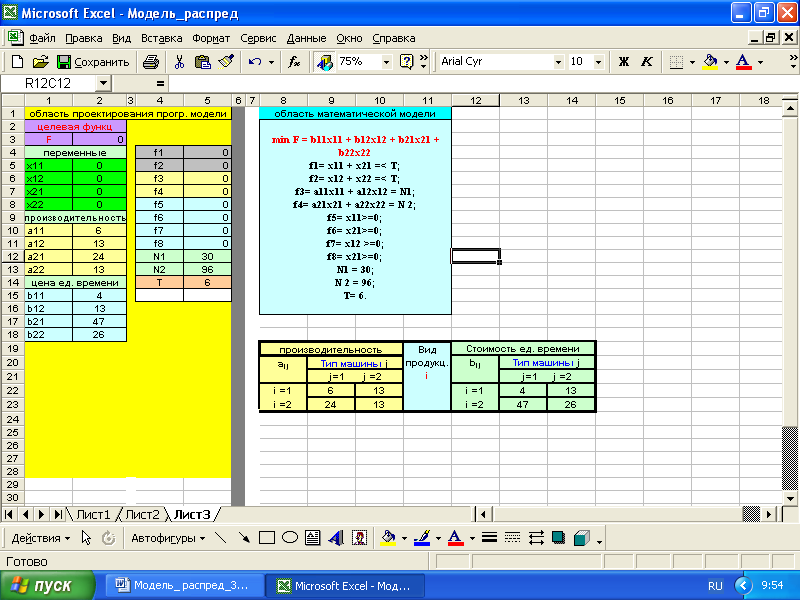
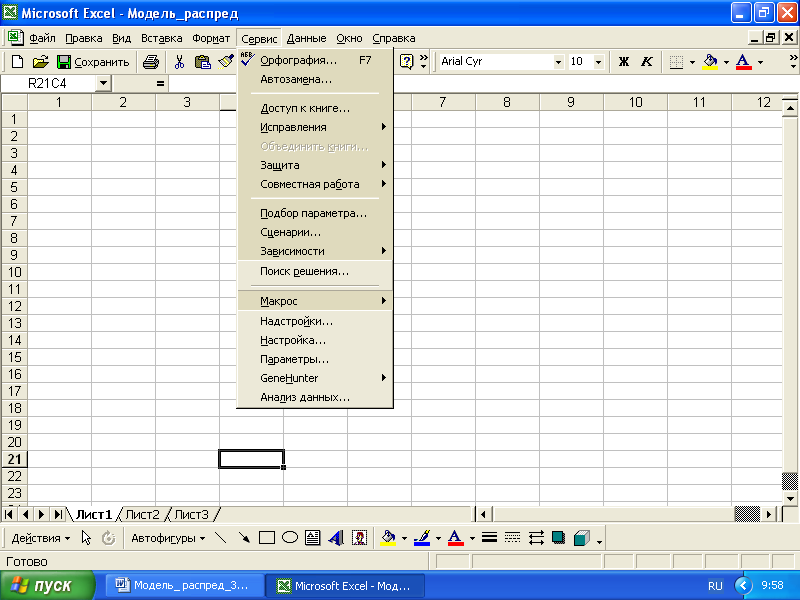
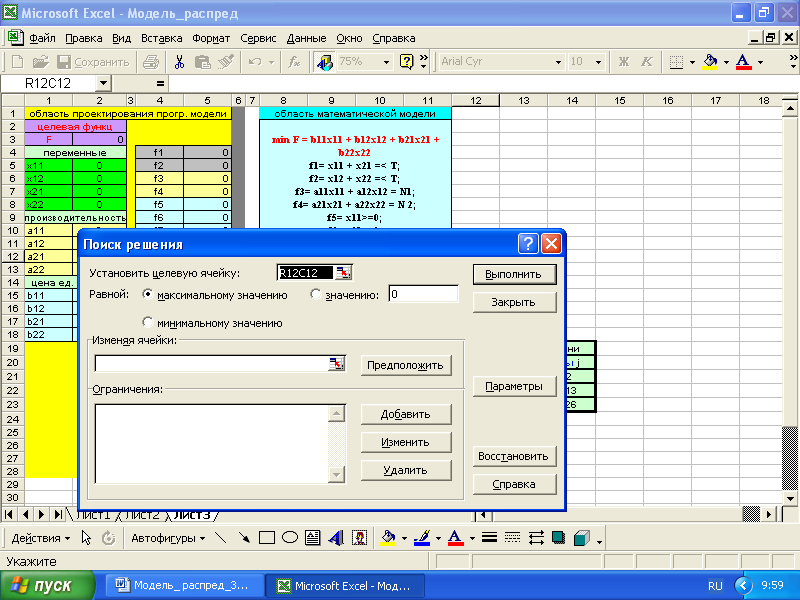
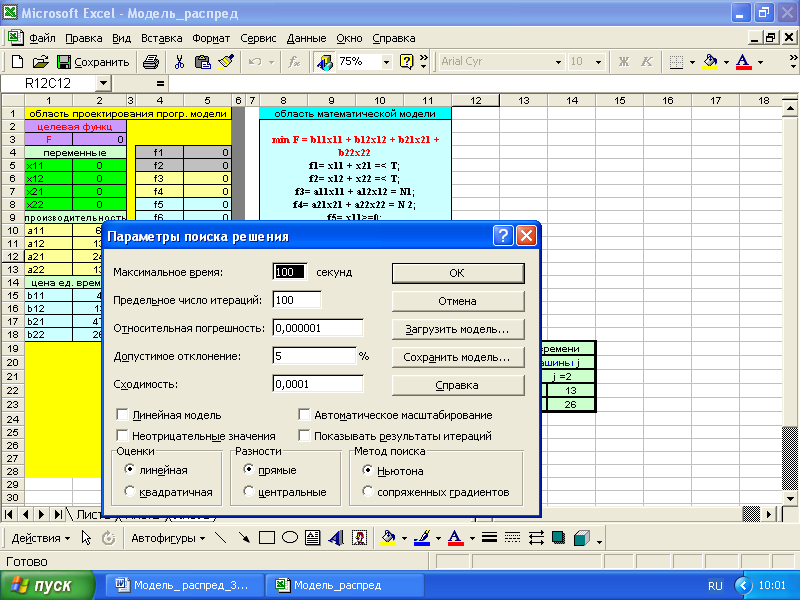
Модель распределения в процедуре эволюционного исчисления Microsoft Excel_2003

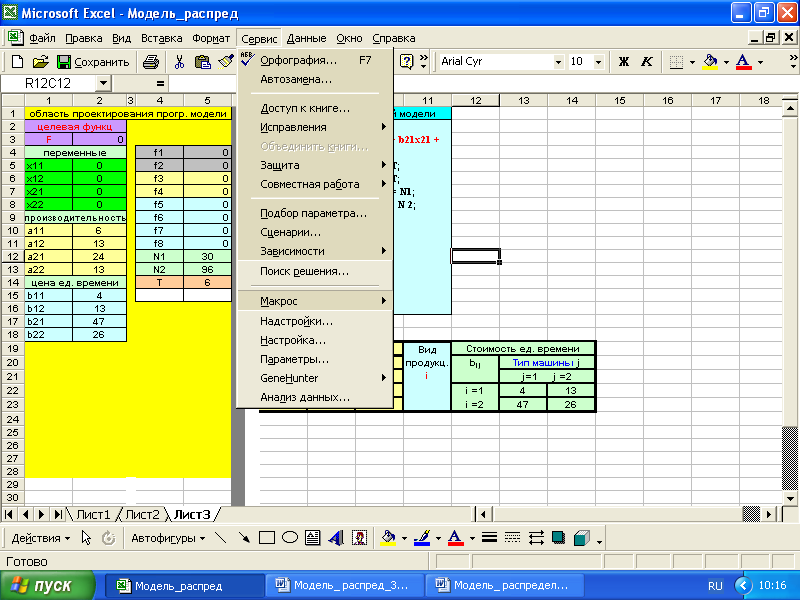
Кодировка ячее в таблицах Excel

row = ряд; строка (R1, R2, …)

column = столбец (C1, C2, …)

Ссылка на ячейку в цифровой кодировке (R1C2)

Ссылка на ячейку в буквенной кодировке ($B$15)

ряд; строка ($1, $2, …)

столбец ($А, $B, …)

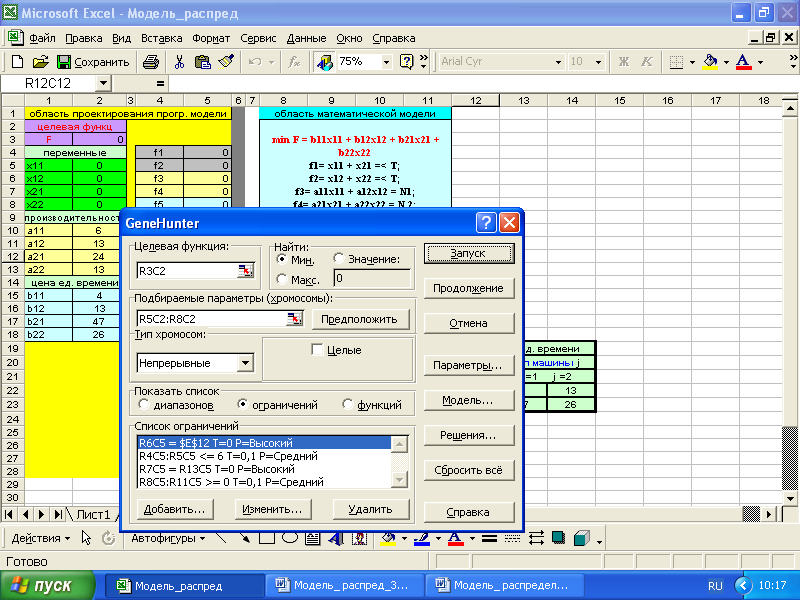
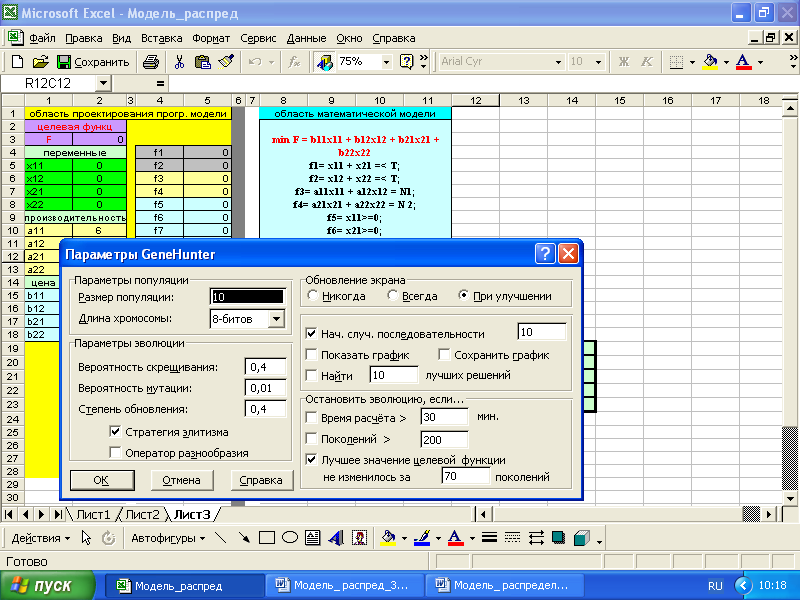
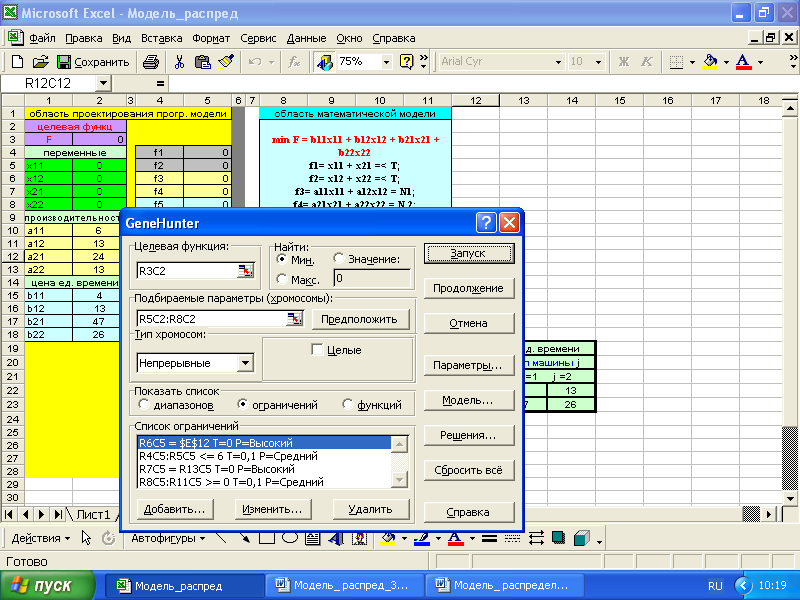
Задание №3

«Модель распределения» в процедуре «Поиск решения» Microsoft Excel_2010

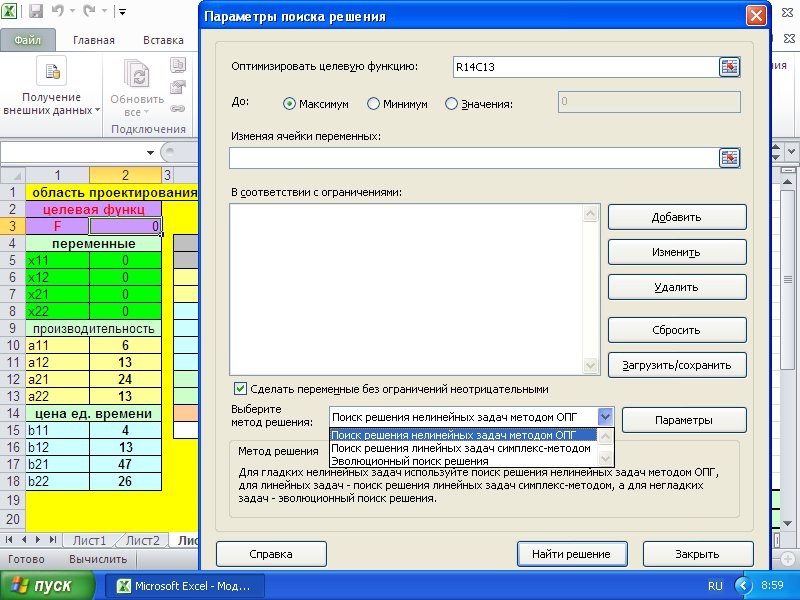
Конец Задания №3

Задание №4

Третий этап — этап верификации математической модели, т.е. выяснение того, удовлетворяет ли принятая (разработанная) модель потребностям практики, т.е. выяснение вопроса о том, что результаты моделирования обладают достаточной правдоподобностью и пригодны для обслуживания (поддержки) процесса управления.

Четвертый этап — тестирование, опытная и рабочая эксплуатация экономико-математической модели. В течение этого этапа происходит накопление данных о применении модели в практической деятельности, и готовятся предложения по последующей модернизация модели, а также проверяется чувствительность модели к изменению исходных данных и нормативных параметров. (Входит в домашнее задание)

Изменение технологических и стоимостных коэффициентов на рабочем листе Microsoft Excel:

производительность				Стоимость ед. времени
аij	Тип машины j			bij	Тип машины j
	j=1 j =2		j=1 j =2
i =1	6	13	Вид продукции i	i =1	4	13
i =2	24	13		i =2	47	26

Объем 1 прод. - f3=а₁₁x₁₁ + а₁₂x₁₂ = N₁ = 30

Объем 2 прод. - f4=а₂₁x₂₁ + а₂₂x₂₂ = N ₂ = 96

Объем 1 прод. - N₁ = А

Объем 2 прод. - N ₂ = Б