95

Лекция 1.

Основные сведения об оптимизационных задачах

Характерной особенностью различных задач оптимизации в науке, механике, инженерной практике является множество возможных вариантов решения таких задач. Эти возможные варианты называют допустимыми решениями задачи. При этом результатом решения задач должен быть единственный, наилучший в некотором смысле, вариант. Он называется оптимальным решением.

Пример задачи оптимизации:

1. Задача оптимального планирования раскроя пиловочного сырья на пиломатериалы.

Предполагается заданным размерно-качественный состав сырья, спецификация пиломатериалов, а также список поставов пригодных к использованию. По результатам решения требуется определить интенсивность использования поставов, т. е. требуется определить объём сырья каждой размерно-качественной группы, который надо распилить по каждому из используемых поставов так, чтобы выход пиломатериалов был максимален, выполнялась спецификация пиломатериалов и учитывались ограничения по объёмам имеющего сырья. Это так называемая содержательная постановка оптимизационной задачи, т. е. постановка её в таком виде, в котором она формируется заказчиком.

Задачи оптимизации решают с применением математических методов, разработанных как в классической математике (дифференциальное исчисления), так и в специальных математических дисциплинах: математическое программирование, теория управления запасами, теория календарного планирования, теория массового обслуживания, теория оптимального управления и т. д. Эти науки обычно объединяют под общим названием «исследование операций». Под операцией здесь понимают совокупность действий, направленных на достижение определенных целей.

Так как методы оптимизации являются математическими, задача оптимизации должна быть сформулирована на математическом языке. Процесс перехода от содержательной к математической постановке называется формализацией задачи. В результате формализации должна быть получена математическая модель задачи.

Математической моделью объекта называется совокупность математических соотношений, описывающий процесс его функционирования.

Математическую модель объектов получают исходя из фундаментальных законов природы и законов физики.

Фундаментальные законы природы это прежде всего законы сохранения материи и энергии. В самом общем виде закон сохранения материи и энергии можно записать следующим образом:

«прибыль» = «убыль» (1.1) для статики и

«прибыль» = «убыль» + приращение (1.2) для динамики.

Практически эти соотношения записывают с использованием понятия «поток вещества». Это количество вещества, проходящее через некоторые сечения в единицу времени. При изучении динамических процессов часто рассматривают не сечения, а некоторую ёмкость.

Рассмотрим пример построения балансовой модели раскроя пиловочного сырья на оборудования агрегатного типа.

Пусть на агрегатном оборудование раскраивают брёвна. Воспользуемся соотношением (1.1 )

В рассматриваемом примере входящий поток – это поток сырья, поступающий в линию. Обозначим объём этого сырья (за какой либо период, например месяц) V₁

Выходящий поток состоит из потока получаемых пиломатериалов, щепы и опилок. Обозначим соответствующие объемы через V₂ (объем пиломатериалов), V₃ ( объем получаемой щепы) и V₄ (объем опилок). Тогда в силу соотношения (1.1) имеем уравнение материального баланса запишется следующим образом:

(1.3)

Взяв производные по времени от обоих частей выражения (1.3), получим дифференциальную форму уравнения:

(1.4)

Уравнение (1.4) задает связь между скоростями изменения входных и выходных потоков, т. е. между производительностью линии по распилу сырья , производительностью по выпуску пиломатериалов, технологической щепы и опилок :

П₁ = П₂ + П₃ + П₄ (1.5)

Рассмотрим еще один пример.

Математическая модель процесса получения проклеенной массы в производстве ДВП.

В ящик непрерывной проклейки, снабженной мешалкой, поступают Q₁ – поток ДВ массы, Q₂ – проклеивающая добавка, Q₃ – гидрофобная добавка, Q₄ – осадитель. В результате перемешивания в резервуаре образуется проклеенная масса Q₅.

Воспользуемся уравнением (1.1)

Q₁ + Q₂ + Q₃ + Q₄ = Q₅ + Q_{5 (1.6)}

Рассмотрим процесс за некоторый единичный промежуток t:

Q₁ + Q₂ + Q₃ + Q₄ = Q₅ + (1.7)

Пусть t 0, тогда получаем дифференциальное уравнение (1.8), являющееся математической моделью объекта:

Q₁ + Q₂ + Q₃ + Q₄ = Q₅ + (1.8)

Лекция 2

Основные принципы построения моделей задач оптимизации.

Задачи оптимизации всегда предполагают получение наилучшего варианта функционирования системы. Количественный показатель, характеризующий качество функционирования системы называется критерием оптимизации (или параметром оптимизации). По этому критерию производится сравнение эффективности различных допустимых решений оптимизационной задачи. К критерию оптимизации предъявляются следующие требования.

Критерий оптимизации должен быть единственным, т.е. выражаться единственным числом. Желательно, чтобы он вычислялся с достаточно высокой точностью, без больших затрат и по возможности всесторонне оценивал эффективность функционирования системы. Критерии оптимизации бывают: экономические (себестоимость, прибыль, рентабельность), технические (надежность, масса изделия и т.п.), технологические (выход, качество продукции и т.п.) и прочие.

Как правило ответ на вопрос, что именно необходимо выбрать в качестве критерия оптимизации содержится в постановке задаче. Так, в примере, рассмотренном в предыдущей лекции требуется найти такой план раскроя «…чтобы выход пиломатериалов был максимален…». То есть, в данной задаче в качестве критерия оптимизации следует использовать выход пиломатериалов, или, как иногда говорят, «решать задачу по критерию максимума полезного выхода».

Этапы построения моделей оптимизационных задач.

1.На первом этапе выбирается критерий оптимизации, который мы здесь и в дальнейшем будем обозначать W.

2. На втором этапе определяются элементы решения задачи. Элементами решения называются переменные ,отыскание значений которых и является целью решения задачи и величина которых определяет значение критерия оптимизации W.

3. На третьем этапе определяется целевая функция модели. Целевой функцией называется зависимость критерия оптимизации от элементов решения

W=f( ) (2.1)

Эту зависимость ищут по результатам теоретических и экспериментальных, а чаще совмещая эти исследования.

4. На четвертом этапе отыскиваются так называемые ограничения модели, т. е. математические выражения в виде равенств и неравенств, учитывающие различные требования к функционированию объекта

(2.2)

………………...

Таким образом, в общем виде, оптимизационную математическую модель можно записать следующим образом:

(2.3)

(2.4)

………………...

В результате решения оптимизационной задачи должны быть найдены такие значения элементов решения , которые удовлетворяют все ограничения (2.4) и доставляют максимум (или минимум, в зависимости от постановки задачи) целевой функции (2.3).

Любое решение, удовлетворяющее все ограничения (2.4) модели называется допустимым решением задачи, а совокупность допустимых решений называется множеством допустимых решений.

При решении оптимизационных задач возможны следующие случаи:

1. Множество допустимых решений не является пустым. Тогда оптимальным является допустимое решение, дающее наилучшее значение целевой функции.

2. Существует только единственное допустимое решение (множество допустимых решений содержит единственный элемент). В этом случае допустимое решение является и оптимальным решением.

3. Допустимых решений не существует (множество допустимых решений пусто). В этом случае оптимизационная задача решений не имеет.

Рассмотрим пример построения оптимизационной модели процесса пиления древесины на лесопильных рамах.

В соответствии с рассмотренной выше последовательностью построения оптимизационной математической модели сначала выбираем критерий W оптимизации процесса. Лесопильная рама является головным оборудованием, которое определяет производительность всего лесопильного цеха. Поэтому в качестве критерия W оптимизации целесообразно использовать производительность П рамы: W=П.

Далее, на втором этапе, определяем элементы решения задачи. В качестве таких элементов решения (от которых зависит производительность лесопильной рамы) выбираем следующие режимные факторы процесса рамного пиления: скорость подачи на один зуб , толщину пил S, шаг зубьев пилы t.

На третьем этапе строится целевая функция модели, то есть ищется зависимость выбранного нами критерия оптимизации (производительности) от элементов решения ( скорости подачи на один зуб , толщины пил S и шага зубьев пилы t ).Производительность П лесопильной рамы ( за смену в погонных метрах распиливаемых брёвен) можно определить по формуле

(2.5)

где к - коэффициент использования оборудования; U-скорость подачи бревен;

Тcм - продолжительность смены.

Скорость U подачи бревен равна

, (2.6)

где n – число оборотов коленчатого вала, мин^-1 ; h – ход пильной рамки;

Подставив выражение (2.6) в (2.5) получаем:

. (2.7)

Так как в результате решения задачи мы должны получить максимальную (с учетом всех ограничений) производительность лесопильной рамы, окончательное выражение для целевой функции задачи будет иметь следующий вид:

(2.8)

Перейдем теперь к четвертому, заключительному этапу на котором формируются ограничения модели. Рассмотрим, сначала, ограничения, введение которых вызваны требованиями к качеству получаемой пилопродукции. Качество пиломатериалов, получаемых в результате распиловки на лесопильной раме характеризуется двумя показателями: шероховатостью поверхности пиломатериалов и их разнотолщинностью. Для оценки шероховатости поверхности пиломатериалов используют среднеарифметическую величину R максимальных высот неровностей. Величина разнотолщинности оценивается величиной среднего квадратического отклонения d толщины пиломатериалов.

Требования к шероховатости поверхности пиломатериалов и точности их размерообразования задаются ограничениями вида

, (2.9)

где – максимально допускаемое значение высот микронеровностей на поверхности доски;

– максимально допускаемое значение среднего квадратичного отклонения толщин досок, а и представляют собой зависимости этих показателей от элементов решения. Их получают по результатам экспериментальных исследований.

Следующая группа ограничений связана с конечным диапазоном варьирования элементов решения и с дискретностью их задания:

< < (2.10)

(2.11)

Ограничение (2.10) задает допустимый диапазон изменения скорости подачи, а ограничение (2.11)- дискретность значений толщин и шага зубьев пилы. Кроме рассмотренных, в модели должны учитываться целый ряд других ограничений, (например по работоспособности впадин зубьев, дискретности величины пути резания) которые для простоты нами опускаются.

Совокупность выражений (2.8) – (2.11) - это оптимизационная модель процесса пиления древесины на лесопильных рамах. В результате ее решения должны быть определены такие значения скорости подачи на зуб, толщины S пил и шаг t зубьев пилы, которые удовлетворяют ограничениям (2.9) –(2.11) и доставляют максимальное значение целевой функции (2.8)

Лекция 3

Модели и методы решения задач линейного программирования. (ЗЛП)

В рамках моделей линейного программирования могут быть сформулированы самые различные по своему содержанию задачи. Рассмотрим несколько примеров.

Задача формирования оптимальной производственной программы мебельной фабрики

Мебельная фабрика выпускает 3 вида продукции (шкафы, столы, стулья). Известны: плановое задания по выпуску изделий каждого вида и прибыль, получаемая фабрикой за выпуск одной единицы каждого из изделий.

Предположим, что в производстве этих изделий заняты станки трёх видов: фрезерные, сверлильные и шлифовальные станки. Известны также затраты машинного времени на изготовление изделий каждого вида по каждой группе станков и общий ресурс станочного времени по каждому станку (см. таблицу. 3.1)

Табл. 3.1

	Шкафы	Столы	Стулья	Ресурс
Фрезерные	0,25	0,18	0,08	160
Сверлильные	0,3	0,2	0,05	180
Шлифовальные	0,35	0,22	0,09	200
План	200	250	300	-
Прибыль	15	9	3	-

В первых трех строках таблицы размещена информация о затратах времени при изготовлении каждого изделия на том или ином станке. Например, при изготовлении одного стола затрачивается 0,2 единиц времени работы сверлильного станка. В строке «план» показано значение планового задания по соответствующему виду изделия, в последней строке– прибыль которую дает производство одного такого изделия (в некоторых условных единицах). В последнем столбце таблицы дается ресурс времени работы каждого станка, т.е. указывается, сколько часов в течении определенного периода могут проработать станки каждой группы.

Требуется определить оптимальную производственную программу предприятия. Тоесть требуется определить, какое количество изделий каждого вида должно выпускать предприятие так, чтобы суммарная прибыль от их производства была максимальной. При этом необходимо выполнение следующих условий:

1. Время работы станков каждой группы не будет превышать имеющихся у этой группы станков ресурса.

2. Количество полученных изделий каждого вида должно быть не менее планового задания по соответствующему виду изделия.

Это содержательная постановка задачи. Построим, теперь, математическую модель задачи.

Начнем с определения критерия оптимизации. В соответствии с условиями задачи, в которых требуется найти такую производственную программу при которой прибыль от производства изделий будет максимальной, в качестве критерия оптимизации выбираем прибыль П предприятия.

На следующем этапе определяем элементы решения задачи. Поскольку мы должны определить оптимальную производственную программу предприятия, т.е. количество изделий каждого вида которое должно выпускать предприятие, в качестве элементов решения выбираем переменные:

- количество шкафов, которые должны выпускаться предприятием;

- количество столов, которые должны выпускаться предприятием;

- количество стульев, которые должны выпускаться предприятием.

Перейдем к построению целевой функции задачи, т. е. к определению зависимости прибыли П предприятия от количества выпускаемых изделий каждого вида.

При производстве одного шкафа предприятие получает прибыль в размере 15 условных единиц. Если производится шкафов, то прибыль от их производства будет в раз больше: 15 . Аналогичным образом, прибыль от производства одного стола равна 9 единицам, а при производстве столов в раза больше: 9 . Прибыль, от производства стульев будет равна 3 , а суммарная прибыль П от производства изделий всех видов будет равна

П =15 + 9 + 3 . (3.1)

Соответственно, целевая функция модели будет выглядеть следующим образом:

W = 15 + 9 + 3 → max (3.2)

Рассмотрим систему ограничений модели. Эти ограничения должны учитывать условие 1 (ограниченность ресурсов времени работы станков) и условие 2 (необходимость выполнения планового задания).

Из табл. 3.1 следует, что при производстве одного шкафа будет затрачено 0,25 единиц времени работы фрезерного станка. Если будет производиться шкафов, то время работы фрезерного станка увеличиться в раз: 0,25 . Фрезерный станок задействован и при производстве столов: на один стол тратиться 0.18 единиц времени, на столов в раз больше: 0.18 . Аналогично, время в течении которого фрезерный станок будет задействован на производстве стульев составит 0.08 , а общее время работы фрезерного станка будет равно сумме 0.25 + 0.18 + 0.08 . Эта сумма должна быть не больше ресурса времени который имеется у этого станка. Следовательно, ограничение по ресурсу времени работы фрезерного станка будет иметь следующий вид:

0.25 + 0.18 + 0.08 ≤160 (3.3)

Таким же образом можно получить и ограничение по ресурсу времени работы сверлильного

0.3 + 0.2 + 0.05 ≤ 180 (3.4)

и шлифовального станков:

0.35 + 0.2 + 0.09 ≤ 200 (3.5)

Более простую форму имеют ограничения, предназначенные для учета второго условия, касающегося выполнения планового задания по выпуску изделий каждого вида. Количество выпущенных шкафов должно быть не менее 200. Из этого условия получаем ограничение:

≥ 200. (3.6)

Количество выпущенных столов должно быть не менее 180, а количество стульев не менее 200. Этим условиям будут соответствовать ограничения

≥ 180, (3.7)

и

≥ 200 (3.8)

Таким образом математическая модель задачи формирования оптимальной производственной программы мебельной фабрики имеет следующий вид:

Целевая функция:

W = 15 + 9 + 3 → max, (3.9)

ограничения:

0.25 + 0.18 + 0.08 ≤160 (3.10)

0.3 + 0.2 + 0.05 ≤180 (3.11)

0.35 + 0.2 + 0.09 ≤200 (3.12)

≥ 200 (3.13)

≥ 180 (3.14)

≥ 200 (3.15)

Совокупность выражений (3.9) –(3.15) это математическая модель задачи составления оптимальной производственной программы мебельной фабрики.

В рассмотренной модели целевая функция, а также функции в левых частях всех ограничений линейны по своим аргументам. По этой причине приведённая модель служит примером модели линейного программирования.

Задача составления оптимального плана поперечного раскроя бревен

Имеются брёвна длиной 6,5м которые необходимо раскроить на кряжи длиной L₁=2м, L₂=2,5м и L₃=1,8м. При том кряжей длиной L₁ необходимо получить в количестве не менее 300шт., L₂- в количестве не мене 250шт., а L₃- не менее 500шт.

Требуется так организовать процесс раскряжевки, чтобы отходы получаемые в результате поперечного раскроя бревен по длине, были минимальны. При этом количество вырабатываемых кряжей каждой длины должно быть не менее заданного.

Построим математическую модель для решения этой задачи. Из ее постановки следует, что в качестве критерия W оптимизации необходимо использовать величину отходов, которую следует минимизировать.

Далее следует определить элементы решения задачи. Для этого, предварительно,

Рассмотрим различные варианты (схемы раскроя) раскряжевки, которые могут быть использованы при поперечном раскрое бревен длиною 6,5 м. (См. Табл.3.2)

Табл.3.2

Вариант	(схема раскроя)	Количество отходов, м
I	2+2+2	0,5
II	2,5+1,8+1,8	0,4
III	2,5+2,5	1,5
IV	2+2+2,5	0,0
V	2+1,8+1,8	0,9
VI	1,8+1,8+1,8	1,1
VII	2+2,5+1,8	0,2
VIII	2+2+1,8	0,7

Вариант N1 предполагает, что из бревен длиною 6,5 м будут получать 3 кряжа, длинною по 2 м. При этом величина отходов по длине составит 0,5 м. При использовании 2-й схемы раскроя вырабатывается 1 кряж длиною 2,5 м и два кряжа длиною 1,8 м. При использовании этой схемы раскроя отходы по длине равны 0,4 м. Оставшиеся варианты также характеризуются величиной отходов, которые получаются в результате использования той или иной схемы раскроя и составом вырабатываемых кряжей различной длины.

Осталось выяснить сколько брёвен следует раскраивать по каждому из предложенных 8 вариантов. Эти переменные и примем в качестве элементов решения. То есть, обозначим через – количество брёвен раскраиваемых по I-у варианту, – по II-у, – по III-у и т. д., – по VIII-у.

Найдем целевую функцию задачи. При раскрое 1-го бревна по 1-й схеме раскроя отходы равны 0,5 м. При раскрое по этой схеме бревен количество отходов увеличится в раз и будет равно 0,5 . При использовании второго варианта при раскрое одного бревна отходы составят 0,4 м, а при раскрое бревен - 0,4 . Аналогичным образом можно найти отходы которые дает использование каждой схемы раскроя. Общая величина отходов будет равна сумме отходов которые получаются при использовании каждой схемы раскроя. Эту величину в соответствии с выбранным критерием оптимизации необходимо минимизировать. Поэтому целевая функция задачи имеет следующий вид:

0,5 + 0,4 + 1,5 + 0 + 0,9 + 1,1 + 0,2 + 0,7 min (3.16)

Запишем ограничения по количеству вырабатываемых сортиментов которое требуется получить в соответствии с условиями задачи. В результате раскроя одного бревна по 1-й схеме раскроя мы получим 3 сортимента длиной 2 метра, а при раскрое бревен количество 2-х метровых сортиментов увеличится в раз и станет равным 3 . Двухметровые кряжи будут получены и в результате раскряжовки по 4-й, 5-й , 7-й и 8 –й схеме раскроя. Количество вырабатываемых при этом 2-х метровых кряжей по каждой схеме указано в табл. 3.2. С учетом этого общее количество 2-х метровых кряжей вырабатываемых по всем схемам раскроя будет равно сумме 3 + 2 + 1 + 1 + 2 . Эта сумма должна быть не меньше требуемого количества двухметровых кряжей. Поэтому ограничение на количество кряжей длиною 2 м запишется следующим образом:

3 + 2 + 1 + 1 + 2 ≥ 300 (3.17)

Аналогичным образом можно получить ограничения на количество вырабатываемых кряжей длиною 2,5 и 1,8 м:

1 + 2 + 1 + 1 ≥ 250, (3.18)

2 + 2 + 3 + 1 + 1 ≥ 500. (3.19)

Значения переменных полученных в результате решения задачи составления оптимального плана раскроя, могут быть только положительные числа или 0:

0 (3.20)

i =

(Запись i = означает, что индекс i изменяется от 1 до 8.) Построенная нами математическая модель также является примером модели линейного программирования.

Лекция 4

Задача о рациональной переработке сырья.

Пусть имеются два предприятия которые занимаются переработкой пиловочного сырья 3-х сортов: 1-го, 2-го и 3-го. В силу различных производственных условий норма выработки продукции на разных предприятиях различны. Обозначим через k₁₁; k₁₂; k₁₃ – коэффициенты объёмного выхода продукции на 1-м предприятии из пиловочного сырья I-го, II-го и III-го сорта, а через k₂₁;k₂₂;k₂₃ – выход продукции на 2-м предприятии из сырья I-го, II-го и III-го сорта соответственно.. Известны предельные мощности и 1-го и 2-го предприятия по переработки сырья, а также общее количество сырья каждого сорта: V₁; V₂; V₃.

Требуется определить, какое количество сырья каждого сорта следует подавать на каждое предприятие, чтобы получить максимальный выход продукции.

При этом необходимо выполнение следующих условий:

1. Общий объем сырья, перерабатываемого на каждом предприятии не должен превышать его предельной мощности.

2. Количество сырья каждого сорта, перерабатываемого на обоих предприятиях, не должно превышать имеющихся запасов сырья данного сорта.

Как следует из постановки задачи ее следует решать по критерию максимального выхода продукции.

Обозначим через ; ; – объемы сырья соответственно I, II и III сорта, поступающие на I-е предприятие, а через ; ;

объемы сырья I, II и III сорта, которое поступает на II-е предприятие.

Количество продукции, которая будет получена на 1-м предприятии из сырья I –го сорта будет равно произведению , а из сырья II-го и III-го сортов - и , соответственно. Аналогично, количество продукции которая будет получена на 2-м предприятии из сырья I-го, II-го и III-го будет равно , и . Общий объем получаемой продукции будет равен сумме + + + + + , для которой требуется найти максимум. Это выражение является целевой функцией W модели:

W = + + + + + → max (4.1)

Перейдем к построению ограничений модели. Количество сырья, перерабатываемого на I-м предприятии равно сумме + +

Это количество не должно превышать предельной мощности первого предприятия:

+ + ≤ (4.2)

Аналогичным образом можно записать ограничение по предельной мощности и для второго предприятия

+ + ≤ (4.3)

Следующая группа ограничений – это ограничения по запасам сырья. Общее количество сырья I-го сорта, поставляемого на 1-е и 2-е предприятие, равно сумме + и не должно превышать имеющегося запаса сырья I-го сорта . Общее количество сырья II-го сорта, поставляемого на 1-е и 2-е предприятие, равно сумме + и не должно превышать имеющегося запаса сырья II-го сорта , а общее количество + сырья III-го сорта - . Следовательно, имеем группу из трех ограничений по запасам сырья каждого сорта:

+ ≤ (4.4)

+ ≤ (4.5)

+ ≤ (4.6)

Кроме того в модели необходимо учесть условия неотрицательности элементов решения:

(4.7)

Построенная модель также является моделью задачи линейного программирования.

Общая постановка задачи линейного программирования.

Как следует из вышеприведенных примеров в рамках задач линейного программирования (ЗЛП) могут быть формализованы самые различные по своему содержанию задачи. Поэтому целесообразно более подробно рассмотреть основные свойства и алгоритм решения таких задач

В общем случае задача линейного программирования (ЗЛП) может содержать произвольное количество n переменных (элементов решения) и также произвольное количество m ограничений, т. е. равенств или неравенств. Рассмотрим такую задачу с ограничениями- неравенствами для случая отыскания max целевой функции.

(4.7)

………………………. (4.8)

(4.9)

Отметим, что в задачах линейного программирования должно выполняться соотношение

m<n,

т.е. количество ограничений должно быть меньше или равно количеству переменных.

Выражение (4.7) является целевой функцией модели, выражения (4.8)- ее ограничениями. Выражение (4.3) является стандартным (тривиальным) ограничением на неотрицательность переменных. В результате решения задачи (4.7- (4.9) должны быть найдены такие неотрицательные

Очень часто для решения задач линейного программирования используются стандартные программные средства, которые предназначены для ЗЛП определенной стандартной формы. Например, программа «RASKR 1» предназначена для решения задач линейного программирования для случая, когда ищется максимум целевой функции, а все ограничения являются равенствами. Если решается, например, задача оптимального раскроя древесно-стружечных плит на мебельные заготовки, в качестве критерия оптимальности используется выход заготовок и требуется точное выполнение спецификации по выпуску заготовок, то соответствующая этой задаче математическая модель будет удовлетворять сформулированным требованиям: целевая функция будет максимизироваться, а все ограничения по количеству получаемых заготовок запишутся в виде равенств. В общем же случае, например при работе по критерию минимума отходов, вид математической модели не будет соответствовать стандартной форме, необходимой для корректного ввода исходных данных в компьютер. Поэтому на этапе подготовки исходных данных для ввода в компьютер необходимо привести исходную математическую модель к стандартной форме. Для этого необходимо использовать следующие правила:

1. Чтобы перейти от минимизируемой целевой функции (типа «min») к максимизируемой (типа «max»), или наоборот, необходимо умножить все коэффициенты целевой функции на “–1”.

2.Чтобы перейти от ограничений-неравенств типа «>» к ограничениям неравенствам типа «<» (или наоборот), необходимо левую и правую части этого ограничения умножить на –1.

Прежде чем перейти к формулировке правил, позволяющих переходить от ограничений в виде неравенств к ограничениям в виде равенств, рассмотрим пример.

Пусть имеется ограничение

3 + 4 ≥ 10 , (4.10)

которое необходимо преобразовать в равенство. Очевидно, что выражение ( 4.10 ) можно записать следующим образом:

3 + 4 = 10 + , (4.11)

где – новая дополнительная переменная, введение которой позволяет представить ограничение (4.12) в виде равенства. Физический смысл переменной прост: она показывает насколько левая часть ограничения (4.11) больше его правой части. Если левая часть равна 10, то = 0.

В моделях линейного программирования переменные всегда находятся в левой части ограничений, а в правой всегда записываются константа. С учетом этого перенесем переменную в левую часть. В результате выражение (4.11) примет следующий вид:

3 + 4 – = 10 (4.12)

Таким образом, чтобы перейти от ограничения типа “≥” к ограничению типа “=” необходимо ввести еще одну, дополнительную переменную. Эта переменная включается в ограничение с коэффициентом “–1”, и имеет индекс на единицу больший чем, наибольший индекс исходного ограничения. Если имеется несколько ограничений, то дополнительны переменные необходимо ввести в каждое ограничение. При этом индекс дополнительной переменной, введенный в какое- либо ограничение должен быть на единицу больше чем индекс дополнительной переменной в предыдущем ограничении.

Аналогичным образом осуществляется переход от ограничений типа “≤” к ограничениям типа “=”. Однако в этом случае дополнительные переменные включаются в исходные ограничения с коэффициентом “1”.

Рассмотрим пример. Пусть имеется задача линейного программирования вида:

2 + 3 – 1 → min (4.13)

1 + 5 + 4 ≤ 80 (4.14)

2 – 4 + 5 ≥ 5 (4.15)

которую необходимо преобразовать к модели с ограничениями в виде равенств.

Введем дополнительные переменные: в неравенстве ( 4.14 ) – , причем с коэффициентом “+1” (т.к. неравенство имеет вид “≤”), а в (4.15) – с коэффициентом “–1” (неравенство имеет вид “≥”).

Функция цели (4.13) стремится к минимуму. Поэтому для перехода к целевой функции типа “max” умножаем все коэффициенты на “–1”. Кроме того, в целевую функцию вводим и дополнительные переменных и , с коэффициентами равными нулю. В результате получаем выражение для целевой функции:

– 2 – 3 + 4 – 0 – 0 → max, (4.16)

и ограничений модели

1 + 5 + 4 + 1 + 0 = 80 (4.17)

2 – 4 + 5 + 0 – 1 = 5 , (4.18)

которые удовлетворяют поставленным условиям.

Лекция 5

Геометрическая интерпретация задачи линейного программирования

Для решения задач ЛП существует универсальный метод, идея которого будет рассмотрена с помощью геометрической интерпретации.

Рассмотрим следующую задачу:

(5.1)

(5.2)

(5.3)

(5.4)

(5.5)

Допустимым решением ЗЛП называется такая совокупность значений переменных , которая удовлетворяет всем ограничениям задачи. Тогда можно сказать, что оптимальное решение задачи ЗЛП – это такое из допустимых решений, при котором значение целевой функции максимально (минимально).

Например: пара чисел =2, =9 не будет допустимым решением , т. к. не удовлетворяет ограничению (5.2) и (5.3), а пара чисел =1, =1 – допустимое решение, так как удовлетворяет всем ограничениям. Решение же =-5, =3 как и любое другое содержащее отрицательное значение переменной, допустимым решением не будет т. к. не удовлетворяет ограничению (5.4) и (5.5).

Будем изображать все возможные решения ЗЛП с 2-мя переменными и точками на координатной плоскости.

В самом деле любая, точка на координатной плоскости характеризуется значением абсциссы и ординаты, т. е . , представляет собой пару чисел, которые можно рассматривать как вариант решения задачи.

Построим координатную плоскость (рис.5.1) у которой по оси абcцисс будут откладываться значения , а по оси ординат – .

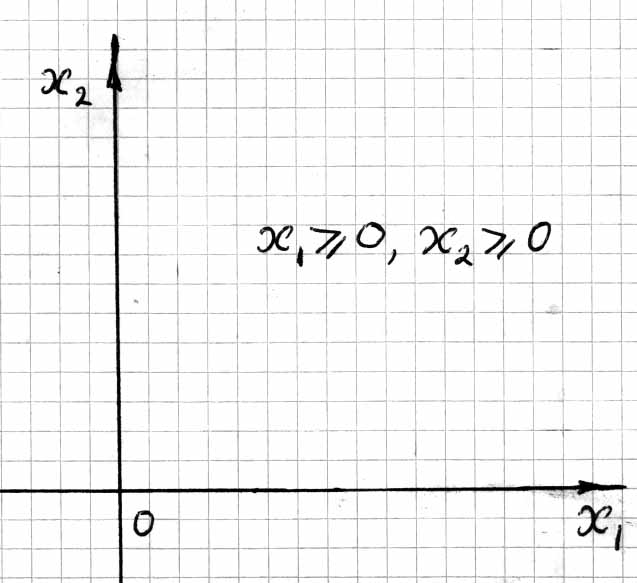
Рис. 5.1

Точки (решения) удовлетворяющие ограничению (5.4) будут находятся правее оси ординат в 1-м и 4-м квадрантах. Ограничению (5.5) удовлетворяют точки (решения) расположенные выше оси абcцисс, в 1-м и 2-м квадрантах. Таким образом решения одновременно удовлетворяющие ограничениям (5.4) и (5.5) находятся в 1-м квадранте. Следовательно, допустимые решения любой задачи линейного программирования всегда находятся в первой четверти координатной плоскости.

Рассмотрим неравенство (5.2). Для этого запишем, сначала, соответствующе равенство

6 + 5 =30 (5.5)

Это уравнение прямой. Чтобы построить эту прямую, достаточно найти координаты двух точек: А и В. (cм. Рис 5.2) В точке А =0. Подставив =0 в выражение (5.5) получаем:

5 =30, (5.6)

Откуда находим :

=6. (5.7)

Следовательно ордината точки А равна 6 . Найдем теперь координаты точки В. Для этого подставим в выражение (5.5) значение =0. Получим

6 =30, (5.8)

Откуда

=5. (5.9)

Следовательно, абcцисcа точки В: =5. Соединив точки А и В получаем прямую АВ. Учитывая знак неравенства ограничения (5.2), можно сделать вывод о том, что точки удовлетворяющие ему, лежат ниже прямой АВ или на ней самой. Одновременно трем (5.2), (5.4) и (5.5) ограничениям удовлетворяют точки лежащие внутри и на границе треугольника ОАВ.

Аналогично учитывается ограничение (5.3). Все точки, для которых оно выполняется, лежат ниже прямой СD или на ней. Уравнение этой прямой

4 + 7 =28, (5.10)

А координаты точек С и D можно найти также, как и координаты точек А и В:

Ордината точки С - =4, а абcцисcа точки D - =7.

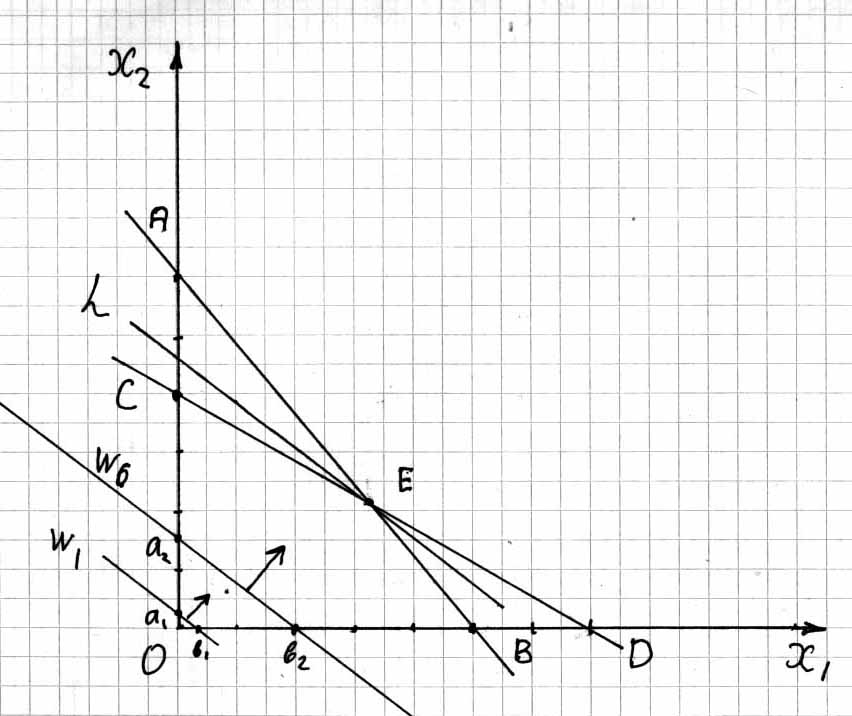
Рис. 5.2

Из рисунка 5.2 видно что точки удовлетворяющие всем ограничениям (5.2) -(5.5) находятся внутри и на границе многоугольника ОСЕВ. Множество этих точек и образуют область допускаемых решений (ОДР). ОДР называется геометрический образ (изображение) множества допускаемых решений.

Оказалось таким образом, что для ЗЛП с 2-мя переменными ОДР – это выпуклый многоугольник на координатной плоскости.

Среди множества допустимых решений необходимо найти оптимальное. Для этого рассмотрим целевую функцию (5.1). Будем придавать ей различные значения и определять, где находятся соответствующие им точки в ОДР. Построим прямую, соответствующую случаю, когда значение целевой функции будет равно 1:

(5.11)

В выражении (5.11) используется индексная переменная , которая показывает, что ищется прямая, которая соответствует значению целевой функции равной 1:

(5.12)

Найдем ординату =0, =1/4 и абcцисcу =0, =1/3 точек пересечения прямой c координатными осями и построим эту прямую на рис.5.2. Среди всех точек этой прямой области допустимых решений принадлежат только точки отрезка , для каждой из которых =1.

Пусть теперь значение целевой W функции равно 6:

(5.13)

Это уравнение* прямой, параллельной предыдущей и расположенной выше

нее. Стрелкой указано направление смещения прямой, соответствующее возрастанию целевой функции. Среди точек этой прямой области допустимых решений принадлежат только точки отрезка . Очевидно, теперь, что максимальное значение целевой функции на множестве допустимых решений достигается при самом верхнем положении прямой W, когда она еще проходит хотя бы через одну точку, принадлежащую ОДР. Это прямая L, проходящая через точку Е. Ее координаты определяются из решения системы уравнений (5.5) и (5.10):

= 3.18, = 2,18. Эта пара чисел является оптимальным решением данной задачи линейного программирования. Значение целевой функции для него равно:

W= 3∙3,18+4∙2,18=18,26 (5.14)

Анализируя полученные результаты можно сделать следующие выводы.

_____________________________________________________________________

* Точки пересечения прямой W c координатными осями можно найти также, как были найдены аналогичные точки для прямой W.

1.Область допустимых решений задачи линейного программирования, если она существует всегда образует выпуклый многогранник в пространстве переменных.

При n=2 - ОДР– выпуклый многоугольник, n=3 – ОДР – выпуклый многогранник в 3^х мерном пространстве.

2.Оптимальное решение, если оно существует, всегда достигается на границе ОДР, а именно в одной из вершин многогранника допустимых решений. Допустимое решение, находящееся в одной из вершин этого многогранника, называется опорным решение, а сама вершина- опорной точкой. В рассмотренном примере вершинам многогранника соответствуют опорные точки ОСЕВ. Поэтому задачу линейного программирования можно решать путем перебора всех вершин (опорных решений) многогранника соответствующего ОДР, выбирая ту вершину, которая соответствует max или min целевой функции..

На этой идее и базируется основной метод решения ЗЛП, называемый симплекс – метод. Согласно этому методу реализуется непростой, а направленный перебор опорных решений, при котором каждому последующему опорному решению соответствует лучшее значение целевой функции.

Рассмотрим различные случаи, которые могут быть при решении ЗЛП.

Случай 1.

ЗЛП имеет единственное решение (см. Пример). Отметим, что при изменении коэффициентов целевой функции изменяется и угол наклона соответствующих ей прямых. Это означает, что оптимально решение может оказаться в другой вершине многогранника. Отметим, также, что изменение коэффициентов целевой функции не приводит к изменению конфигурации ОДР, и наоборот, при изменении коэффициентов ограничений конфигурация ОДР изменяется. Знание этих свойств ЗЛП помогает проводить анализ результатов ее решения, в частности результатов решения задач раскроя в деревообработке.

Случай 2.

ЗЛП не имеет решений. Это может быть в 2^х случаях:

А) Множество допустимых решений пусто. Например, система ограничений задачи имеют вид

(5.15)

(5.16)

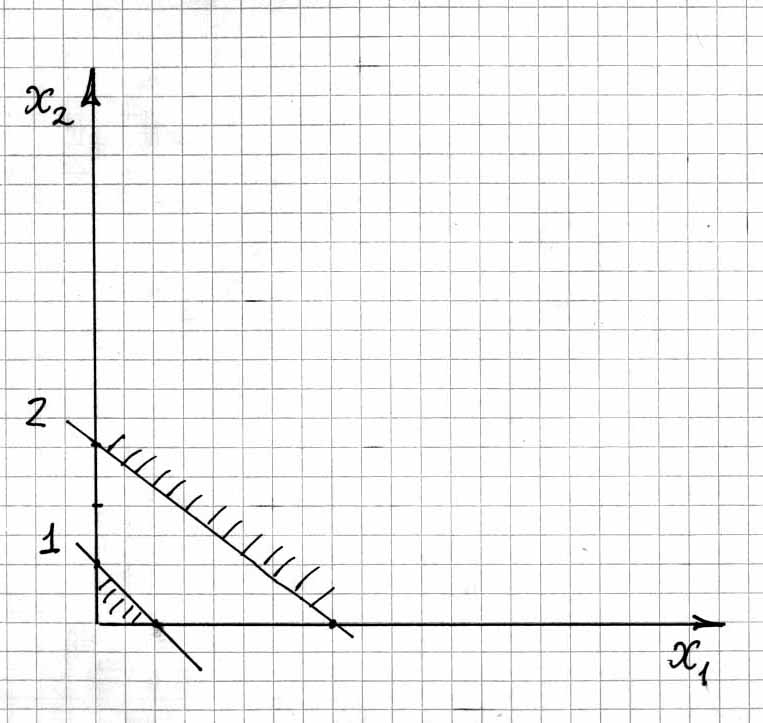
Рис. 5.3

Эта система не имеет решений, поэтому допустимых решений задачи не существует. Как видно из рис. 5.3, точки удовлетворяющие первому ограничению (выражение (5.15), находятся ниже прямой 1, а допустимые решения удовлетворяющие второе ограничение (выражение (5.16)), выше прямой 2.

Б) Целевая функция не ограничена, т.е. Может принимать сколь угодно большие значения. Этот случай иллюстрирует следующий пример:

Рис. 5.4

Геометрическая интерпретация для этого случая показана на рис 5.4 Из рисунка видно, что значение целевой функции не ограничено и она может принимать сколь угодно большие значения.

Случай 3

Оптимальное решение в некоторых случаях может лежать не только в вершине многогранника, но и в точках на некотором его ребре. В этом случае задача имеет не одно, а множество решений. Так, например, произойдёт если в предыдущем примере ( 5.1 )- (5.5 ) прямая W будет параллельна отрезку АВ (см. рис5.2).

Например выражение для целевой функции будет иметь вид:

W=6 +5 max

В этом случае оптимальным решением будет любая точка отрезка АВ. Такой случай называется вырожденным.