
Вариант 4-12
I часть: запишите ответ на бланке № 1.
1. Найти
значение выражения
|
1б |
2. Найдите сумму наибольшего общего делителя и наименьшего общего кратного чисел 180 и 270. |
1б |
||
3. Решите
уравнение
|
1б |
4. Вычислите
|
1б |
||
|
1б |
6. Найдите
произведение корней уравнения
|
1б |
||
7. Точка К лежит на отрезке MN, длина которого 16, причем MK:KN=3:2. Найдите расстояние MK. |
1б |
8. Найдите
значение выражения
|
1б |
||
9. Решите
уравнение
|
1б |
10. Вычислите
|
1б |
||
11. Укажите
наименьшее целое решение неравенства
|
2б |
12. На сколько процентов уменьшится число 16, если из него вычесть число 4? |
2б |
||
13. Найдите два числа, если их произведение равно 6, а сумма равна –5. |
2б |
14. Найдите
значение функции
|
2б |
||
15. Решите
уравнение
|
2б |
16. Из формулы
|
2б |
||
17. Сколько лотерейных билетов можно купить на 200 рублей, если 4 таких билета стоят 78 рублей? |
2б |
18.
Решите систему
уравнений
|
2б |
||
19. В первый день продавец сумел продать 84% имеющегося товара, а во второй – остальные 32 кг. Сколько всего килограммов товара было у продавца? |
2б |
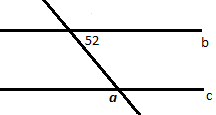
20. Стороны параллелограмма 7 и 15. Найдите длины отрезков, на которые делит большую сторону биссектриса большего угла параллелограмма. |
2б |
II часть: запишите решение заданий на бланке № 2.
1. Найдите сумму
целых чисел, входящих в область
определения функции
|
4б |
2. При каких
значениях х дробь
|
4б |
3. Две снегоуборочные машины, работая вместе, могут очистить от снега площадь за 12 часов. Если бы сначала первая машина выполнила половину работы, а затем вторая закончила бы уборку снега, то на всю работу ушло бы 25 часов. За сколько часов могла бы очистить эту площадь каждая машина, работая отдельно? |
5б |
4. При каких
значениях а система
|
5б |
5. Расстояние от
общей хорды двух пересекающихся
окружностей до их центров относятся
как 2:5. Общая хорда имеет длину
6. Постройте
график функции
|
6б |
6б |

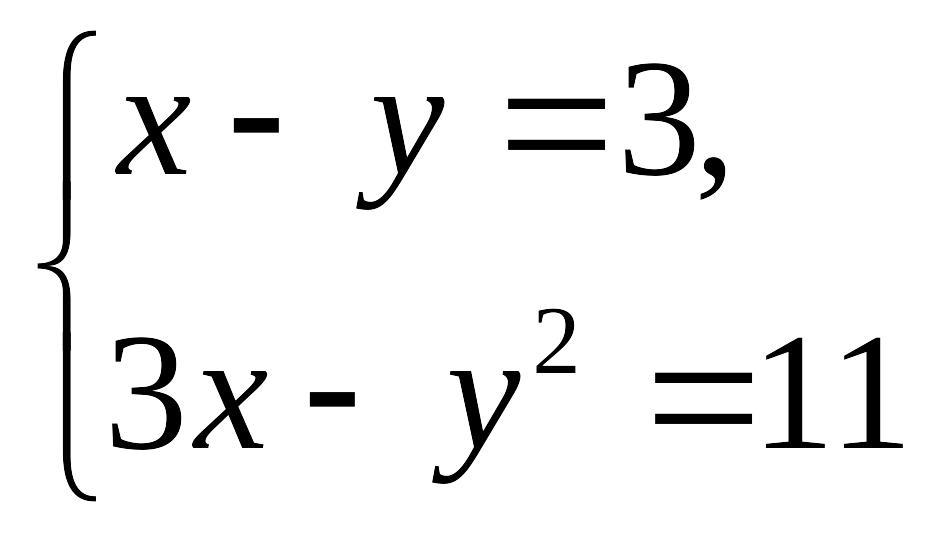 и сложите все получившиеся значения
х
и у.
и сложите все получившиеся значения
х
и у.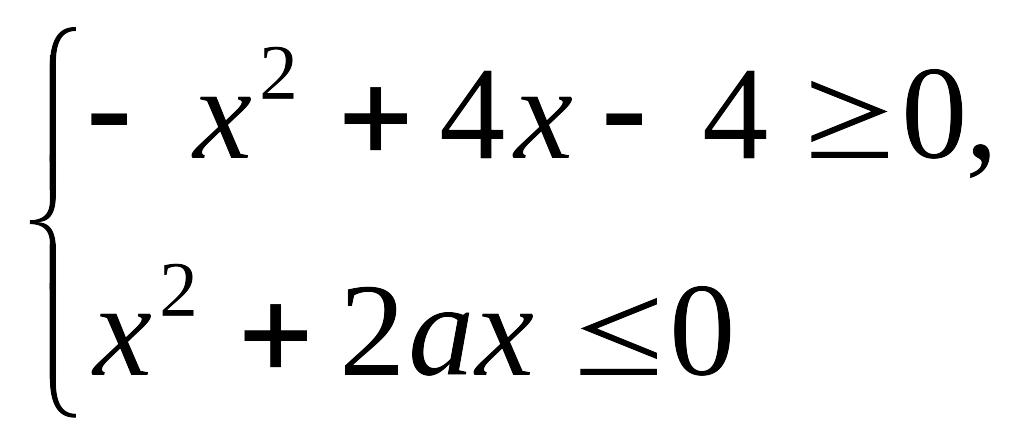 имеет решения?
имеет решения?