- •Тема: Расчет коэффициента корреляции и уравнение регрессии.
- •Рекомендации по выполнению
- •Построение линейного уравнения парной регрессии по .
- •1Способ (с помощью добавления тренда):
- •2Способ (с помощью функций):
- •3Способ (с помощью инструмента анализа данных Регрессия):
- •4Способ (с помощью вычислений):
- •Задача анализа временных рядов
- •Статистические функции в Excel
- •Значение критерия Стьюдента (t-критерия) Стьюдента (n – число наблюдений , m – число факторов)
- •Критические значения коэффициента Стьюдента (t-критерия) для различной доверительной вероятности p и числа степеней свободы f:
3Способ (с помощью инструмента анализа данных Регрессия):
Использовать инструмент анализа данных Регрессия для получения: результатов регрессионной статистики, дисперсионного анализа, доверительных интервалов, графиков подбора линии регрессии, остатков и нормальной вероятности.
 Порядок
действий следующий: вкладка
Файл/Параметры/Надстройки/нажать
Перейти/ в окне Надстройки установить
флажок
Пакет анализа/ нажать
ОК
и вкладка
Данные/ группа Анализ / Анализ данных /
в окне Анализ данных выбрать
Регрессия
и нажать
ОК.
Порядок
действий следующий: вкладка
Файл/Параметры/Надстройки/нажать
Перейти/ в окне Надстройки установить
флажок
Пакет анализа/ нажать
ОК
и вкладка
Данные/ группа Анализ / Анализ данных /
в окне Анализ данных выбрать
Регрессия
и нажать
ОК.
Рисунок 11 – Параметры Excel
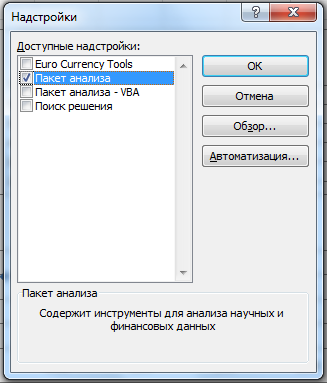
Рисунок 12 - Надстройки
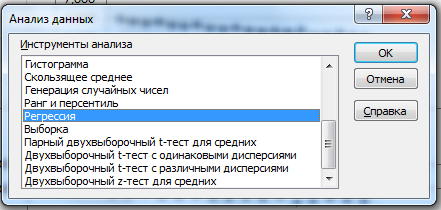
Рисунок 13 –Анализ данных
Появится диалоговое окно Регрессия входных данных и параметров вывода. Необходимо заполнить в нем пустые поля.
Входной интервал у – диапазон, содержащий данные результативного признака;
Входной интервал х – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа - ноль – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении регрессии;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно создать произвольное имя нового листа.
Замечание. Если необходимо получить информацию об остатках и графики остатков, установите соответствующие флажки в диалоговом окне.
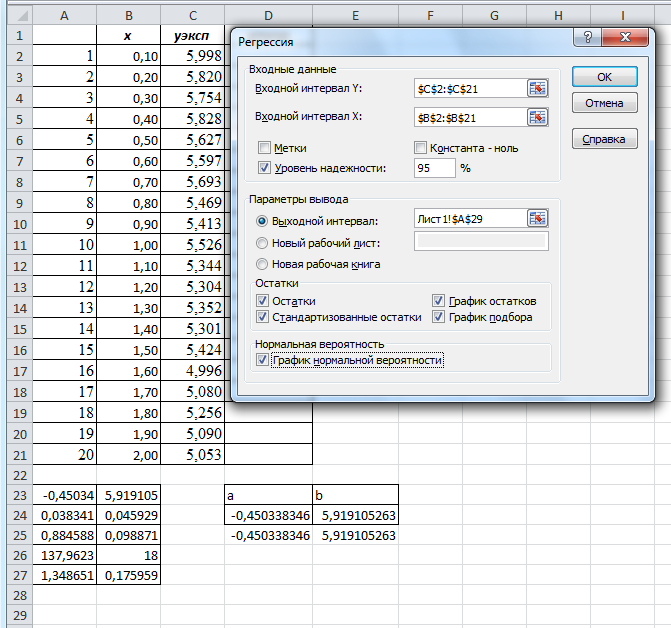
Рисунок 14 - Диалоговое окно ввода параметров инструмента РЕГРЕССИЯ
Результаты регрессионного анализа:
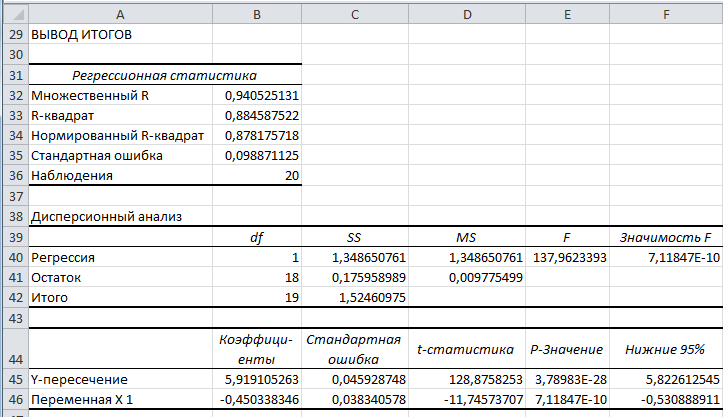
Рисунок 15 - Результат применения инструмента Регрессия
Остальные результаты применения инструмента Регрессия представлены в приложениях Б, В, Г.
4Способ (с помощью вычислений):
Аналитический
способ нахождения значений
 .
.
Построить таблицу вида:
x
y эксп=
yi
y теор=
y(xi)
yi*xi
xi^2
yi^2
(yi-ycp)^2
(yi-y(xi))^2
(xi-xcp)^2
|yi-y(xi)|:yi
№
1
2
…
20
сумма
xcp
ycp
Среднее значение
Вычислить значения с помощью формул (2) и (3) – см. стр. 4.
№2 Рассчитать линейный коэффициент парной корреляции, коэффициенты детерминации (обычный и исправленный) и среднюю ошибку аппроксимации.
Выборочные средние:
xср = ∑xi / n = 21 / 20 = 1.05; yср = ∑yi / n = 108.93 / 20 = 5.45; xyср = ∑xiyi / n = 111.38 / 20 = 5.57
Выборочные дисперсии:
S2(x) = ∑x2i / n - x2ср = 28.7 / 20 - 1.052 = 0.33 S2(y) = ∑y2i / n - y2ср = 594.76 / 20 - 5.452 = 0.0762
обозначение |
Значение |
Вычисление |
Линейный коэффициент парной корреляции (rxy) |
-0.9405 |
КОРРЕЛ(диапазон X; диапазон Y)
|
Коэффициент детерминации обычный (R2) |
0.8846 |
Рассчитан (см. рис.15 и 14, таб.3)
|
Коэффициент детерминации исправленный (нормированный) (R2скор,
|
0,8782 |
Рассчитан (см. рис.15)
где m - количество объясняющих переменных модели (число факторов), n – число наблюдений. |
Средняя
ошибка аппроксимации ( |
1.44% |
|
Коэффициент регрессии ( ) |
-0.45 |
Рассчитан (см. рис.15, 14, 7 и формулу (2) |
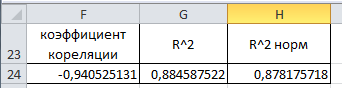

Рисунок 16 - Результат расчета коэффициентов
Величина влияния фактора на исследуемый отклик может быть оценена при помощи коэффициента линейной парной корреляции, характеризующего тесноту линейной связи между двумя переменными.
Коэффициент обладает следующими свойствами:
1) не имеет размерности, следовательно, сопоставим для величин различных порядков;
2) изменяется в диапазоне от –1 до +1. Положительное значение свидетельствует о прямой линейной связи, отрицательное – об обратной. Чем ближе абсолютное значение коэффициента к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент по абсолютной величине превышает 0,7, и слабая, если он менее 0,3. Качественная оценка тесноты связи величин Х и Y может быть оценена на основе шкалы Чеддока:
Тестона связи |
Значение коэффициента корреляции |
Слабая |
0,1-0,3 |
Умеренная |
0,3-0,5 |
Заметная |
0,5-0,7 |
Высокая |
0,7-0,9 |
Весьма высокая |
0,9-0,99 |
Как
известно, прямая линия описывается
уравнением вида (1).
В нашем примере параметры
уравнения регрессии
 ,92
где
–
результирующий
признак,
–
факторный
признак,
и
–
числовые
параметры уравнения
(
есть наклон,
– константа данной парной регрессии).
Коэффициент
в
уравнении регрессии называется
коэффициентом
регрессии.
,92
где
–
результирующий
признак,
–
факторный
признак,
и
–
числовые
параметры уравнения
(
есть наклон,
– константа данной парной регрессии).
Коэффициент
в
уравнении регрессии называется
коэффициентом
регрессии.
Смысл коэффициента регрессии
В общем случае коэффициент регрессии показывает, как в среднем изменится результативный признак ( Y ) (понизится - «-», повысится – «+»), если факторный признак ( X ) увеличится на единицу.
Линейный коэффициент корреляции |
Теснота связи между признаком и фактором весьма высокая, направление связи - обратная. |
Коэффициент регрессии |
Интерпретации коэффициента регрессии. По имеющимся наблюдениям, при повышении величины фактора на 1 единицу (ед. изм.) понижается в среднем на 0.45 (ед. изм.). |
Свойства коэффициента регрессии
• Коэффициент регрессии принимает любые значения.
• Коэффициент регрессии не симметричен, т.е. изменяется, если X и Y поменять местами.
• Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения X ([ Y ] / [ X ]).
• Коэффициент регрессии изменяется при изменении единиц измерения X и Y .
Сравнение коэффициентов корреляции и регрессии
Коэффициент корреляции |
Коэффициент регрессии |
|
|
Средняя
ошибка аппроксимации - среднее
отклонение расчетных значений от
фактических.
|
С помощью ошибки абсолютной аппроксимации производят оценку качества уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации. Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии. |
Множественный коэффициент R = 0,9405 |
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции. |
Коэффициент детерминации обычный R 2=0.8846 |
88.46%
вариации зависимой переменной ( |
Cкорректированный (нормированный, исправленный) коэффициент детерминации R2скор= |
Если значения обычного и исправленного коэффициентов детерминации различаются незначительно, а также R2 >= R2скор и их значения велики, то считается, что регрессия аппроксимирует эмпирические данные достаточно точно и тем теснее наблюдения примыкают к линии регрессии. |
 показывает
качество подгонки. Чем ближе значение
к 1, тем ближе модель к собранным
наблюдениям.
показывает
качество подгонки. Чем ближе значение
к 1, тем ближе модель к собранным
наблюдениям.
В
регрессионном анализе коэффициент
детерминации
свидетельствует
о качестве регрессионной модели и
отражает долю общей вариации результирующего
признака
,
объясненную
изменением функции регрессии
 .
Справедливо соотношение 0<=R2<=1.
Чем ближе этот коэффициент к единице,
тем больше уравнение множественной
регрессии объясняет поведение
.
.
Справедливо соотношение 0<=R2<=1.
Чем ближе этот коэффициент к единице,
тем больше уравнение множественной
регрессии объясняет поведение
.
Замечание. Если R2 > 0.8, то качество подгонки регрессионной модели к наблюденным значениям yi считается хорошим. Чем ближе коэффициент детерминации к единице, тем лучше точки на регрессионном поле укладываются на линию регрессии, т.е. тем выше уровень «подгонки» модели (Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение y).
Если
R2
< 0.5,
то модель надо улучшить либо выбрав
другие факторы, либо увеличив количество
наблюдений (при
функциональной связи между переменными
R2
равняется 1(эмпирические
точки
 расположены на линии регрессии),
а при отсутствии связи — 0)
.
расположены на линии регрессии),
а при отсутствии связи — 0)
.
Для
того чтобы исследователи не увеличивали
R2
с помощью добавления дополнительных
факторов, R2
заменяется
на скорректированный Adjusted R-squared
(обозначение:
![]() или R2скор),
который даёт штраф за дополнительно
включённые факторы.
или R2скор),
который даёт штраф за дополнительно
включённые факторы.
Для небольших значений n (<30) необходимо использовать скорректированный коэффициент детерминации.
![]() для
m>1,
где m
– количество факторов. Скорректированный
коэффициент детерминации является
более объективной оценкой. С ростом
значения m скорректированный коэффициент
детерминации растет медленнее, чем
обычный. Добавление в модель новых
объясняющих переменных осуществляется
до тех пор, пока растет скорректированный
коэффициент детерминации. Очевидно,
что
для
m>1,
где m
– количество факторов. Скорректированный
коэффициент детерминации является
более объективной оценкой. С ростом
значения m скорректированный коэффициент
детерминации растет медленнее, чем
обычный. Добавление в модель новых
объясняющих переменных осуществляется
до тех пор, пока растет скорректированный
коэффициент детерминации. Очевидно,
что
![]() только
при R2
= 1.
может принимать отрицательные значения.
только
при R2
= 1.
может принимать отрицательные значения.
Из двух вариантов уравнений, которые отличаются величиной скорректированного коэффициента детерминации, но имеют одинаково хорошие другие критерии качества, предпочитают вариант с бóльшим значением скорректированного коэффициента детерминации.
Если величина скорректированного коэффициента детерминации достаточно велика, следовательно, при построении модели были учтены наиболее существенные факторы.
Замечание. Величина коэффициента детерминации R2 имеет смысл только в том случае, когда константа включена в состав регрессоров, и может быть интерпретирована как доля вариации зависимой переменной, объясненная вариацией независимых переменных (факторов) регрессионного уравнения.
№3 Произвести оценку параметров уравнения регрессии.
Поскольку проверка гипотез основана на предположении о нормальности распределения ошибок регрессионного уравнения, необходимо проверить его выполнение для полученного вектора остатков регрессии.
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
t-статистика. Критерий Стьюдента.
Выполнить проверку нулевой гипотезы H0 о равенстве нулю некоторого коэффициента регрессионного уравнения (H0: βi=0).
ПЕРВЫЙ СПОСОБ
Необходимо сравнить фактическое значение статистики с критическим значением t-статистики Стьюдента для выбранного уровня значимости ε, то есть со значением двусторонней (1-ε) квантили t-статистики Стьюдента с n-k степенями свободы.
Величина ε характеризует допустимый уровень вероятности ошибиться, отвергнув нулевую гипотезу, когда она верна. В теории проверки статистических гипотез величину ε называют ошибкой первого рода.
Если фактическое значение t-статистики Стьюдента больше критического значения статистики, то нулевая гипотеза отвергается для данного уровня значимости ε, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости ε.
В случае отклонения нулевой гипотезы для уровня значимости ε говорят, что коэффициент βi (a или b) регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента βi (a или b) значимо отличается от нуля) и соответствующий ему регрессор объясняет вариацию зависимой переменной. В противном случае говорят, что коэффициент незначим на уровне значимости ε.
ВТОРОЙ СПОСОБ
Необходимо сравнить p-значение (фактическую вероятность принятия нулевой гипотезы данного коэффициента регрессии) с выбранным уровнем значимости ε. Если выполняется условие p<ε, то нулевая гипотеза отвергается на уровне значимости ε, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости ε.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
р-значение |
Y-пересечение |
5,919105263 |
0,045928748 |
128,8758253 |
3,78983E-28 |
Переменная X1 |
-0,450338346 |
0,038340578 |
-11,74573707 |
7,11847E-10 |
Нулевая гипотеза (Н0): = -0.45 равен 0
1 способ |
2 способ |
tf=|-11,74573707|>tkr=2.101 |
P=7,11847E-10 <0.05 |
нулевая гипотеза отвергается для данного уровня значимости ε |
нулевая гипотеза отвергается для данного уровня значимости ε |
коэффициент регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента ) значимо отличается от нуля) |
коэффициент регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента значимо отличается от нуля) |
Н0: = 9.9191 равен 0
1 способ |
2 способ |
tf=|128,8758253|>tkr=2.101 |
P=3,78983E-28 <0.05 |
нулевая гипотеза не отвергается для данного уровня значимости ε |
нулевая гипотеза отвергается для данного уровня значимости ε |
коэффициент регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента значимо отличается от нуля) |
коэффициент регрессионного уравнения значим на уровне значимости ε (или, говорят, что оценка коэффициента ) значимо отличается от нуля) |
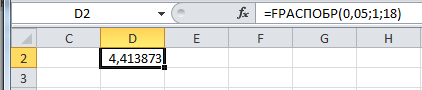
tкрит (n-m-1;α/2) = (18;0.025) = 2.101 |
|
|
|
|
|
Для
нахождения табличного (критического)
значения критерия Стьюдента определяют
число степеней свободы, которое
определяется по формуле
 ,
и находят его значение при определенном
уровне значимости (например, 0,10; 0,05;
0,01).
,
и находят его значение при определенном
уровне значимости (например, 0,10; 0,05;
0,01).

Рисунок 17 - Расчет критического значения t-статистики Стьюдента
Расчёт критического значения t-статистики Стьюдента смотрите в приложении Д.
Доверительный интервал для коэффициентов уравнения регрессии (самостоятельно рассчитать): (b - tкрит Sb; b + tкрит Sb), (a - tкрит Sa; a + tкрит Sa).
2) F-статистика. Критерий Фишера.
Статистика Фишера F (для проверки гипотезы о значимости уравнения в целом)
H0: { β1=β2=…=0}, то есть тестируется одновременное равенство нулю всех коэффициентов регрессионного уравнения кроме константы регрессии .
1 СПОСОБ
Необходимо сравнить фактическое значение статистики Фишера Fф, с критическим значением статистики Фишера Fкр для выбранного уровня значимости ε, то есть со значением (1-ε) квантили статистики Фишера с (n-k, k-1) степенями свободы.
Если фактическое значение статистики Фишера F больше критического значения, то нулевая гипотеза отвергается для данного уровня значимости ε, иначе нулевая гипотеза не может быть отвергнута для данного уровня значимости ε.
В случае отклонения нулевой гипотезы для уровня значимости ε говорят, что регрессионное уравнение значимо в целом на уровне значимости ε и вариация независимых переменных объясняет вариацию зависимой переменной в регрессионном уравнении. В противном случае говорят, что уравнение в целом незначимо на уровне значимости ε и включенные в регрессию факторы не улучшают прогноз для зависимой переменной по сравнению с ее средним значением.
2 СПОСОБ
Воспользовавшись вторым методом тестирования гипотез для рассматриваемого примера, если получим, что p-значение для статистики Фишера Prob(F-statistic) близко к нулю, то это означает, что на любом достаточно малом уровне значимости α можно отвергнуть тестируемую нулевую гипотезу.
F |
Значимость F |
137,9623393 |
7,11847E-10 |
Н0: =0
1 способ |
2 способ |
|
P=7,11847E-10 < 0.05 |
нулевая гипотеза отвергается для данного уровня значимости ε |
нулевая гипотеза отвергается для данного уровня значимости ε |
регрессионное уравнение значимо в целом на уровне значимости ε и вариация независимых переменных объясняет вариацию зависимой переменной в регрессионном уравнении |
регрессионное уравнение значимо в целом на уровне значимости ε и вариация независимых переменных объясняет вариацию зависимой переменной в регрессионном уравнении |
Расчет фактического значение критерия Фишера вычисляют следующим образом:
n – число наблюдений, m – число факторов.
|
|
Рисунок 18 - Расчет фактического значение критерия Фишера
Табличное (критическое) значение критерия Фишера вычисляют следующим образом:
Табличное значение критерия со степенями свободы k1=1 и k2=18, Fтабл = 4.41 |
|
Рисунок 19 - Расчет табличного значение критерия Фишера
Определяют
 ,
которое равно количеству факторов (
).
Например, в однофакторной модели (модели
парной регрессии)
,
которое равно количеству факторов (
).
Например, в однофакторной модели (модели
парной регрессии)
 ,
в двухфакторной
,
в двухфакторной
 .
.
Определяют
 ,
которое определяется по формуле
,
где n - число наблюдений, m - количество
факторов. Например, в однофакторной
модели
,
которое определяется по формуле
,
где n - число наблюдений, m - количество
факторов. Например, в однофакторной
модели
 .
.
На пересечении столбца и строки находят значение критерия Фишера
Оценка уравнение в целом
При оценке значимости коэффициента линейной регрессии на начальном этапе можно использовать следующее грубое правило, позволяющее не прибегать к таблицам.
Если стандартная ошибка коэффициента больше его модуля (|t| < 1), то коэффициент не может быть признан значимым, т.к. доверительная вероятность здесь при двусторонней альтернативной гипотезе составит менее чем 0.7.
Если 1<|t|<2, то найденная оценка может рассматриваться как относительно (слабо) значимая. Доверительная вероятность в этом случае лежит между значениями 0.7 и 0.95.
Если 2<|t|<3, то это свидетельствует о значимой линейной связи между X и Y. В этом случае доверительная вероятность колеблется от 0.95 до 0.99.
Наконец, если |t|> 3, то это почти гарантия наличия линейной связи.
Конечно, в каждом конкретном случае играет роль число наблюдений. Чем их больше, тем надежнее при прочих равных условиях выводы о значимости коэффициента. Однако для n >10 предложенное грубое правило практически всегда работает.
№4 На одном графике отложить исходные данные и теоретическую прямую. Спрогнозировать значение функции еще на два шага вперед от максимального .

Рисунок 20 - Исходные и рассчитанные данные
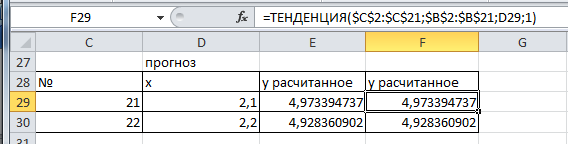
Е29: =$D$24*D29+$E$24
Замечание. Прогноз на следующий период: ТЕНДЕНЦИЯ(диапазон Y; диапазон X; новое значение Х).
Онлайн решение: http://math.semestr.ru/corel/corel.php
ПРИЛОЖЕНИЕ А


 или
или
 )
)
 )
)
 )
объясняется вариацией независимой
переменной (
).
Остальные 11,54% вариации зависимой
переменной объясняются другими
факторами, неучтенными в модели.
Другими словами - точность подбора
уравнения регрессии – высокая.
)
объясняется вариацией независимой
переменной (
).
Остальные 11,54% вариации зависимой
переменной объясняются другими
факторами, неучтенными в модели.
Другими словами - точность подбора
уравнения регрессии – высокая. 0,8782
0,8782

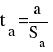
 =137,9623393
>
Fkr=4,41
=137,9623393
>
Fkr=4,41