Вариант 7

В1. Каждый день во время конференции расходуется 80 пакетиков чая. Конференция длится 6 дней. Чай продается в пачках по 25 пакетиков. Сколько пачек нужно купить на все дни конференции?

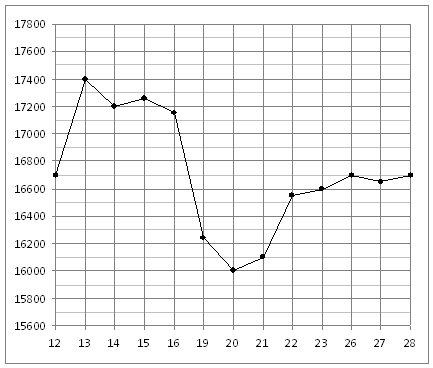
В2. В сентябре 1 кг помидоров стоил 80 рублей, в октябре помидоры подорожали на 20%, а в ноябре еще на 25%. Сколько рублей стоил 1 кг помидоров после подорожания в ноябре? В3. На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 12 по 28 ноября 2007 года. По горизонтали указываются числа месяца, по вертикали — цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода цена олова на момент закрытия торгов была от 16500 до 17000 долларов США за тонну.

В4. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 11 тонн природного камня и 7 мешков цемента. Для бетонного фундамента необходимо 8 тонн щебня и 57 мешков цемента. Тонна камня стоит 1550 рублей, щебень стоит 630 рублей за тонну, а мешок цемента стоит 240 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?

В5. Периметры двух подобных многоугольников относятся как 1:3. Площадь меньшего многоугольника равна 12. Найдите площадь большего многоугольника.

В6. В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,3. Вероятность того, что чай закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня чай останется в обоих автоматах. В7. Найдите корень уравнения 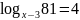. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

В8. Площадь ромба равна 147. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.

В9. На рисунке изображён график функции y=f(x). Пользуясь рисунком, вычислите, F(6)-F(2) , где F(x) — одна из первообразных функции f(x)

.

В10. Около шара описан цилиндр, площадь поверхности которого равна 66. Найдите площадь поверхности шара.

В11. Найдите значение выражения

В12. Трактор тащит сани с силой F= 40 кН, направленной под острым углом α к горизонту. Мощность (в киловаттах) трактора при скорости v= 6 м/с равна N= F v cosα . При каком максимальном угле α (в градусах) эта мощность будет не менее 120 кВт?

В13. Найдите угол B₁ AC₁ прямоугольного параллелепипеда, для которого AB=12, AD =13, AA₁ =5. Ответ дайте в градусах.

В14. Из пункта A круговой трассы выехал велосипедист. Через 20 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 5 минут после отправления он догнал велосипедиста в первый раз, а еще через 8 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 8 км. Ответ дайте в км/ч.

В15. Найдите наибольшее значение функции .

С1. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку .

С2. В правильной четырехугольной пирамиде MABCD с вершиной М стороны основания равны 6, а боковые ребра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку С и середину ребра МА параллельно прямой BD.

С3. Решите систему неравенств

С4. Две окружности пересекаются в точках Р и Q. Прямая, проходящая через точку Р, второй раз пересекает первую окружность в точке А, а вторую- в точке D. Прямая, проходящая через точку Q параллельно АD, второй раз пересекает первую окружность в точке В, а вторую – в точке С. а) Докажите, что четырехугольник АВСD – параллелограмм. б) Найдите отношение ВР:РС, если радиус первой окружности вдвое больше радиуса второй.

C5. Найдите все значения а, при каждом из которых уравнение имеет единственный корень.

С6. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы ( по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число , выписанное на доску, повторяется на доске несколько раз, то на доске оставляют одно такое число , а остальные числа, равные , стираются. Например, если задуманы числа 1,3,3,4, то на доске будет выписан набор 1,3,4,5,6,7,8,10,11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2,4,6,8.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1,3,4,5,6,9,10,11,12,13,14,17,18,19,20,22?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 9,10,11,19,20,21,22,30,31,32,33,41,42,43,52.