Приклади розв’язання задач

Задача 1. Акціонерне товариство "Холдингова компанія "Київміськбуд" випустило 1 тисячу привілейованих акцій номіналом 10 грн. Мінімальний річний прибуток при емісії акцій було оголошено рівним 25 % від їх номіналу. Чистий прибуток товариства складає 5000 грн. Визначити мінімальну суму, яку товариство повинно сплатити кожного року у вигляді дивідендів за привілейованими акціями та прибуток на прості акції.

Рішення:

Дивіденд на одну акцію дорівнює:

Б, = 10 х 25/100 = 2,5 грн.,

тоді величина дивіденду за всіма випущеними привілейованими акціями буде дорівнювати:

1000 х 2,5 = 2500 грн.

Прибуток на прості акції — це різниця між чистим прибутком і виплаченим дивідендом за привілейованими акціями.

П(ЗА) = 5000 - 2500 = 2500 грн.

Задача 2. Акціонерний комерційний банк "Імплексбанк" на акції номіналом 1 тис. грн., курсова вартість яких на початку року становила 2 тис. грн, виплачував дивіденди щокварталу за ставками 13, 16, 20 і 26 % річних відповідно. Курс долара на початку року складав 4,6 грн./$, а в кінці кожного наступного кварталу — 5,8, 5,1, 5,3 і 5,5 грн./$ відповідно. Визначити прибутковість за рівнем дивіденду акцій, куплених на початку року.

Рішення:

Розмір дивіденду за акціями товариства щоквар­тально складає:

1. кв.: 0,25 0,13 1000 = 325 грн.;

2. кв.: 0,25 0,16 1000 = 400 грн.;

3. кв. :0,25 0,2 1000 = 500 грн.;

4. кв.: 0,25 0,26 1000 = 650 грн.

Тоді розмір дивідендів за рік:

325 +400 +500 +650 = 1875 грн.

Так як прибутковість за рівнем дивіденду визначається відношенням розміру дивіденду до курсової вартості акції, тоді Іе - 1875/2000 = 0,9375 або 93,75 %.

Задача 3. Прибуток за облігаціями товариства з обмеженою відповідальністю "Будмеханізація" номіналом 10000 грн. виплачується два рази на рік, виходячи з 45 % річних. Визначити суму прибутку при кожній виплаті. Як зміниться прибуток, якщо виплати будуть чотири рази на рік з розрахунку 50 % річних.

Рішення:

Сума прибутку виходячи, з 45 % річних:

І₁= 0,5 х 0,45 х 10000 = 2250 грн.

Якщо виплати будуть чотири рази на рік з розрахунку 50 % річних, то сума прибутку буде дорівнювати

І₂ = 0,25 х 0,5 х 10000 = 1250 грн.

Задача 4. Припустимо, що випущено 15%-ву облігацію з номіна­льною вартістю 1000 грн. До терміну її погашення зали­шається 5 років. У даний час облігація оцінюється в 915 грн. Визначте прибутковість до погашення (заявлену прибут­ковість) цієї облігації.

Рішення:

Заявлена прибутковість облігацій може бути визначена в такий спосіб:

,

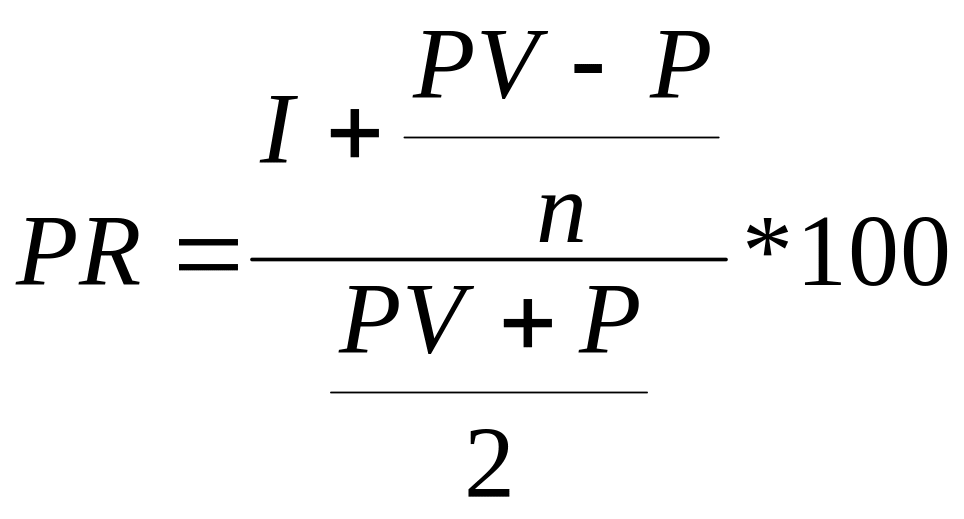де І — номінальна прибутковість; PV — номінал облігації; Р — курс облігації; n — число років до погашення облігації.

Отже, для нашої задачі І = 15%; PV=1000 грн.; Р = 915 грн.; n = 5.

Використовуючи формулу, отримаємо:

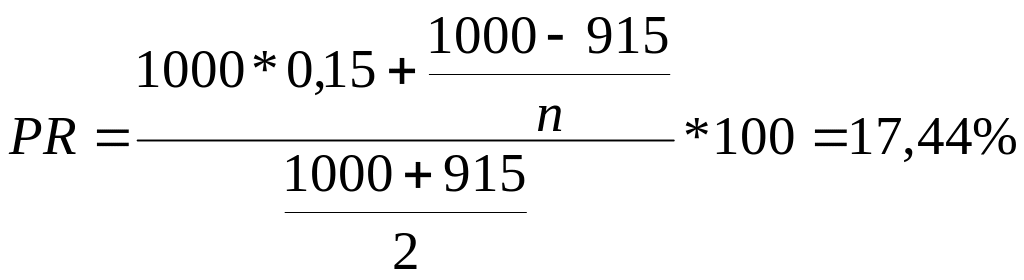
Задача 5. Визначіть, як зміниться вартість 8%-ї облігації через З роки, якщо відомо, що в даний час вона оцінюється в 985 грн., термін її обігу – 5 років, номінал – 1000 грн. Розрахуйте поточну, заявлену і реалізовану прибутковість облігації.

Рішення:

Визначимо поточну прибутковість облігації за формулою:

,

де І – номінальна прибутковість; Р – курс облігації.

Для нашої задачі І = 8% * PV; PV=1000 грн.; Р = 985 грн.; n = 5.

Визначимо заявлену прибутковість облігації за формулою (див. попередню задачу):

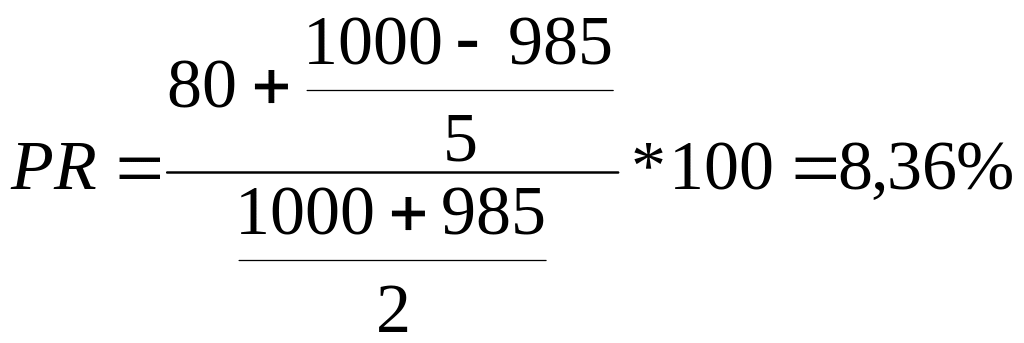
Визначимо реалізовану прибутковість облігації за формулою (n_volod=3):

,

де n_volod – число років володіння облігацією.

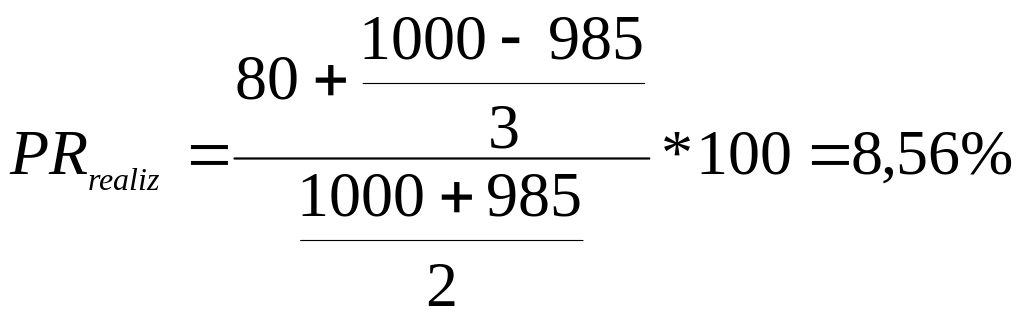
Задача 6. Інвестор здійснює трирічну безризикову інве­стицію в розмірі 10000 грн. у папери з фіксованим доходом. У перший рік ставка відсотка становила 7%, у другий — 8% і в третій — 9%. Кожна купонна виплата може бути реінвестова-на за ставкою, яка буде діяти в році, що настає після цієї ви­плати. Припускаючи нарахування складних відсотків і випла­ту вкладеної суми наприкінці третього року, визначіть: до якої величини збільшиться інвестована сума через три роки? Зробіть розрахунок майбутньої вартості грошей через три роки, якщо складні відсотки нараховуються кожен квартал.

Рішення:

Позначимо первісну інвестицію через Р = 10000 грн., процентну ставку через г. Тоді г₁ = 7%, г₂ = 8%, г₃= 9%.

Для визначення величини прибутку від інвестицій з фіксованим доходом використовують формулу майбутньої вартості, яка обчислюється на основі складних відсотків:

,

де F_n – майбутня вартість поточної суми грошей; Р – дійсна (поточна) вартість (наприклад, сума первісного внеску на депозит); r – процентна ставка; n – число років; t – періодичність нарахування відсотків протягом року.

Якщо відсотки нараховуються кілька разів на рік, то F_n дорівнює:

Визначимо майбутню вартість інвестованої суми грошей через три роки за умови, що відсотки нараховуються щороку за різними шкалами:

F =10000 *(1 + )¹ * (1 + )¹ * (1 + )¹ = 12596,04 грн.

Обчислимо майбутню вартість інвестованої суми грошей через три роки за умови, що відсотки нараховуються кожен квартал за різною шкалою:

F =10000 *(1 + )^1*4 * (1 + )^1*4 * (1 + )^1*4 = 12689,77 грн.