3 Структурная схема эмс и расчет передаточных функций

Для расчета всех передаточный функций блоков структурной схемы, воспользуемся прикладной программой “ Расчет схемы замещения АД”.

Рис 3.1 Скриншот программы для расчета параметров схемы замещения АД

Данные двигателя:

Номинальная мощность Pн=30 кВт

Номинальное линейное напряжение Uн=380 В

Номинальная частота сети fc=50 Гц

КПД=0,89

Cos fi=0.84

Число пар полюсов 3

Номинальная частота вращения ротора np=975 об/мин

Кратность пускового тока 6,5

Кратность пускового момента 2,1

Кратность критического момента 2,2

Момент инерции ротора J=0.9 кг*

Номинальный ток статора Is=60,43 A

Номинальный ток ротора Ir=42,3 A

Ток холостого хода Ixx=55 A

Активное сопротивления статора Rs=0.145 Ом

Активное сопротивления ротора Rr=0.098 Ом

Реактивное сопротивления статора Xs=0.363 Ом

Реактивное сопротивления ротора Xr=0.502 Ом

Главная взаимная индукция:

Рассчитаем коэффициент рассевания статора:

Рассчитаем коэффициент рассевания ротора:

Рассчитаем коэффициент электромагнитной связи ротора:

Рассчитаем коэффициент электромагнитной связи статора:

Рассчитаем коэффициент рассевания по Блонденна:

Индуктивность фазы статора и ротора:

Электромагнитное постоянная времени в роторе:

Эквивалентное сопротивление двигателя:

Эквивалентное электромагнитное постоянное времени статора:

Необходимые параметры для построение модели двигателя:

Расчет преобразователя частоты:

Передаточная функция управляемого выпрямителя:

Параметры фильтра:

Эквивалентное сопротивление объекта АИН-АД

Расчет регуляторов

Рассчитаем регулятор выпрямленного тока:

Постоянная времени фильтра:

Передаточная функция регулятора тока:

Передаточная функция регулятора напряжения:

После определения всех необходимых параметров составляем модель двигателя и запускаем его без нагрузки. Так как модель работает удовлетворительно далее определяем передаточные функции датчиков и согласующих устройств.

Рис 3.2 Модель АД в Matlab в соответствии к структуре

3.3 Передаточная функция датчиков и согласующих устройств:

Рассчитаем датчик скорости:

Рассчитаем датчик тока:

Рассчитаем датчик напряжения:

3.4 Передаточная функция преобразователя

Расчет преобразователя частоты:

Передаточная функция управляемого выпрямителя:

Параметры фильтра:

Рис 3.3 Модель ПЧ в Matlab

Р ис 3.4 модель Matlab Simulink

3.5 исследование устойчивости неизменной части аналитическими методами

Проверим устойчивость по критериям Найквиста:

Если изменять частоту ω от -∞ до ∞, то вектор W (jω) будет изменятся по величине фазе. Кривую, описываемую концом вектора в комплексной плоскости, называют амплитудно-фазовой характеристикой разомкнутой системы.

Амплитудно-фазовая характеристика симметрична относительно вещественной оси, поэтому обычно вычерчивают только ту часть ее, которая соответствует положительным частотам ω>0, а ветвь этой характеристики, соответствует отрицательным частотам ω<0, может быть найдена как зеркальное отражение ветви, соответствующее положительным частотам, относительно вещественной оси.

Для устойчивости замкнутой системы необходимо и достаточно, что бы все корни ее характеристического уравнения были левыми. Таким образом, если разомкнутая система является неустойчивой и имеет l правых корней, то замкнутая система будет устойчивой тогда и только тогда, когда амплитудно-фазовая характеристика вспомогательной функции φ(jω) при изменении частоты ω от 0 до ∞ охватывает начало координат в положительном направлении l/2 раз.

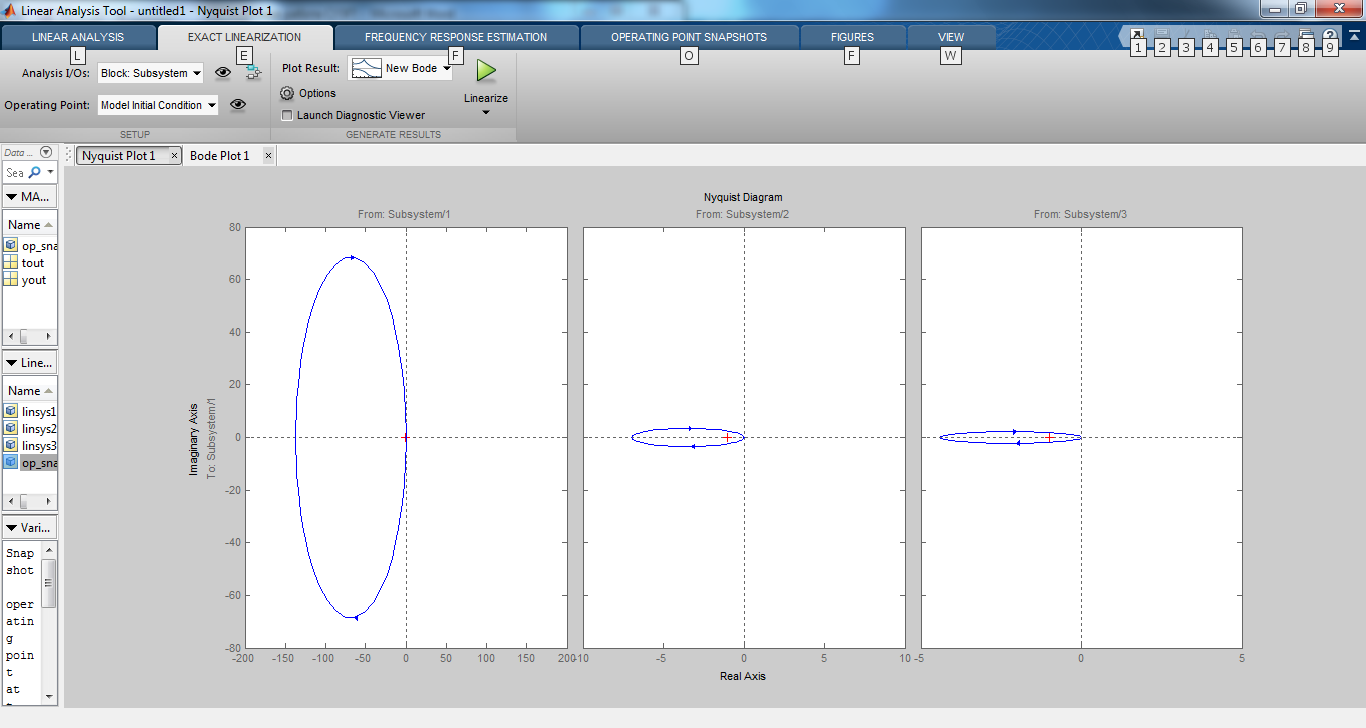
График 3.1 Графики устойчивости объекта по Найквисту

Проверим устойчивость по критериям Боде:

Логарифмические амплитудные и фазовые частотные характеристики (ЛЧХ),

называемые диаграммами Боде.

Прологарифмировав выражение частотной характеристики (через амплитудную и фазовую), получим, что ее логарифм равен сумме логарифма амплитудной характеристики и фазовой характеристики:

.

Две характеристики  и  , построенные в логарифмическом масштабе частот ( ), называются натуральными логарифмическими амплитудными и фазовыми частотными характеристиками.

Точка, соответствующая нулевому значению частоты лежит слева в бесконечности, т.к. lg0 = -¥. Поэтому ось ординат проводится через любую точку оси частот так, чтобы справа располагалась та часть ЛЧХ, которую нужно исследовать, а слева – для описания которой достаточно качественных характеристик. Слева обычно остается та часть фазовой характеристики, которая мало отличается от нуля (или другого постоянного значения). То же самое можно сказать и о коэффициенте наклона амплитудной характеристики. Слева обычно оставляют ту часть амплитудной характеристики, коэффициент наклона которой мало отличается от нулевого значения (или другого постоянного значения.

Амплитудную и фазовую характеристики изображают на одном рисунке с общей осью частот. Ось частот разбивается на декады и, может быть, октавы, причем каждая декада разбивается на октавы отдельно. Обе характеристики имеют общую ось ординат, но две разные разметки: в децибелах для амплитудной характеристики и в радианах (или градусах) для фазовой.

Удобство логарифмических характеристик заключается в возможности простого определения амплитудных характеристик последовательного соединения звеньев и спрямления амплитудных характеристик, как будет показано ниже. Передаточная функция последовательного соединения звеньев равна произведению передаточных функций соединяемых звеньев. Поэтому

.

Вместе с тем

.

,

Таким образом, логарифмические характеристики последовательного соединения складываются. Это относится как к амплитудным, так и к фазовым характеристикам.

График 3.2 Графики устойчивости объекта по Боде