4.2.4 Шар в однородном поле.

Посмотрим, какие изменения внесет проводящий шар, помещенный в однородное электрическое поле. Данная задача весьма популярна, известно несколько принципиально различных методов ее решения. Мы же воспользуемся уже полученными нами результатами. Поместим шар посредине между двумя одинаковыми по величине, но противоположными по знаку точечными зарядами и . Обозначим расстояния от зарядов до центра шара (рис.24).

Построим изображения каждого заряда в шаре - два заряда, величины которых равны , и расположены на расстоянии . Теперь мысленно начнем уносить заряды на бесконечность . При этом заряды-изображения будут приближаться к центру шара, образуя точечный диполь с дипольным моментом

. (29)

При увеличении расстояния между зарядами поле в области шара становится практически однородным с напряженностью

. (30)

Выразим индуцированный дипольный момент шара через напряженность поля

, (31)

как видите этот дипольный момент не зависит от «придуманных» зарядов и расстояния , поэтому и в однородном поле шар будет иметь такой же дипольный момент. Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно полю точечного диполя (31), находящегося в центре шара. Ну а поле диполя мы уже рассчитывали, поэтому приводим результат расчета силовых линий суммарного поля: исходного однородного и индуцированного (рис.25). Неплохо также смотрится и распределение потенциала (рис.26).

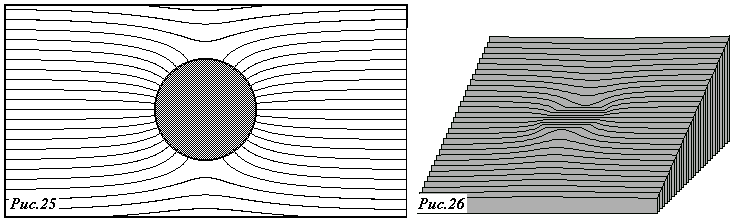
Замечу, что потенциал однородного поля изменяется по линейному закону, поэтому распределение потенциала в таком поле изображается наклонной плоскостью. При помещении в это поле проводящего шара на наклонной плоскости появляется горизонтальная площадка, соответствующая условию постоянства потенциала на проводнике.

Задание для самостоятельной работы.

1. Постройте силовые линии электрического поля, если в изначально однородное поле помещен шар, изготовленный из диэлектрика с проницаемостью . Внимательно, посмотрите на наш переход от проводящей плоскости к полупространству, заполненному диэлектриком.

4.2.5 Электрическое взаимодействие двух сфер.

Рассмотрим взаимодействие двух шариков, один из которых имеет заряд , а второй заземлен.

В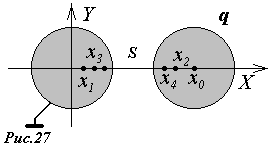 берем систему координат, как показано на рис.27. Обозначим расстояние между центрами шаров , а их радиусы примем равными 1. Идея расчета базируется на методе изображений. Поле заряженного уединенного металлического шарика эквивалентно полю точечного заряда. Поэтому поместим в центр этого шарика точечный заряд, величину которого определим позднее. Далее построим цепочку зарядов-изображений, последовательно отражая заряд в шариках³, величины и положения этих зарядов следует рассчитывать по формулам построения изображений в сфере:

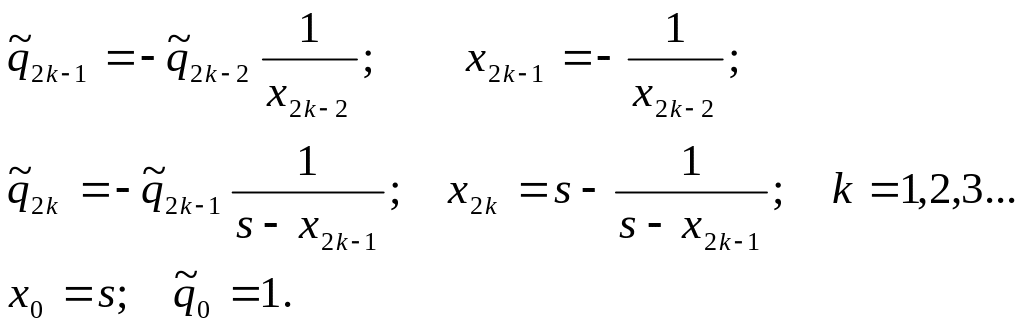(32)

Первая строчка описывает заряды в левом, заземленном шарике, вторая в правом, заряженном. Теоретически число этих изображений должно быть равным бесконечности. Однако величины зарядов убывают приблизительно в геометрической пропорции, поэтому при расчетах можно ограничиться конечным числом изображений, которой нам удобно обозначить .

Вспомните, при построении изображения в незаземленной сфере появляется два заряда-изображения, один из которых находится в центре сферы. Именно поэтому мы заранее не можем сказать, чему равен этот центральный заряд. Физическая причина этой проблемы - перераспределения заряда шарика. Величины остальных зарядов пропорциональны величине центрального заряда (обозначим ее ). Для определения этой величины воспользуемся постоянством полного заряда шарика (который равен сумме зарядов-изображений в этом шарике, то есть нечетным их отображениям):

, (33)

из этого соотношения находим искомый центральный заряд и затем пересчитываем все остальные заряды

(34)

Таким образом, мы окончили построение цепочки зарядов. Обратите внимание на необходимость перенормировки величин зарядов - она у нас встретится и в дальнейшем.

Процедура рисования силовых линий по известным заряда нам давно знакома, поэтому можете посмотреть на результаты при различных значениях расстояния между центрами шаров (рис.28). Расчет проведен при . При сближении шаров заряды и электрическое поле все больше концентрируются в области между шарами.

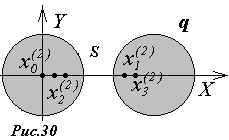
Уберем заземление шара, при этом будем считать, что он электрически нейтрален. В этом случае расчет поля усложняется - появляются изображения и в центре нейтрального шара. Поэтому нам необходимо построить две цепочки зарядов - каждая из которых начинается в центре своего шара. Цепочка, начинающаяся из центра правого шарика, описывается формулами (см. рис.29)

(35)

Вторая цепочка, начинающаяся с левого шарика, строится аналогично (рис. 30):

(35)

Как и в предыдущем случае, нам неизвестны величины центральных зарядов . Поэтому необходимо провести перенормировку зарядов, используя условия постоянства зарядов шариков:

(36)

Неизвестные величины можно найти, решив данную систему уравнений, после чего следует пересчитать все заряды

. (37)

Результаты расчета поля при (всего 202 заряда) приведены на рис. 31.

С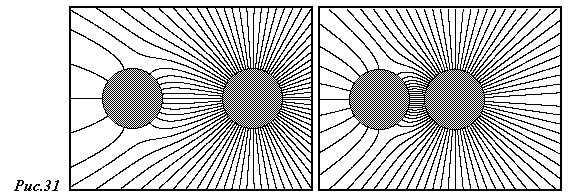 равните эти картинки с предыдущими и найдите не менее 10 различий.

Задание для самостоятельной работы.

1. Вычислите силу действующую между шариками, во всех рассмотренных случаях.

1 Прежде всего, честно признаемся, что данное предположение фактически является попыткой угадать решение, правда затем эта догадка будет строго доказана.

2 Полная аналогия с оптическими изображениями в параллельных зеркалах.

3 Аналогично построению цепочки изображений в двух параллельных плоскостях.

192