§ 4.2 Метод изображений в электростатике.

Мы рассмотрели несколько задач расчета электростатических полей при известном распределении зарядов. В такой ситуации решение задачи представляет собой чисто техническую вычислительную проблему, потому, что с физической точки зрения решение сводится к использованию закона Кулона и принципа суперпозиции. К сожалению, достаточно часто встречаются ситуации, когда распределение зарядов заранее неизвестно. Типичный пример такой ситуации - расчет поля в присутствии проводников и диэлектриков, на поверхности которых индуцируются заряды, распределение которых неизвестно. Однако в таких случаях известны физические законы, которые связывают между собой индуцированные заряды и характеристики поля - напряженность и потенциал (так называемые граничные условия). Наиболее просто граничное условие звучит для проводников - поверхность проводника является эквипотенциальной. Знание граничных условий позволяет переформулировать математическую постановку задачи и воспользоваться иными методами. Одним из самых известных способов расчета полей является метод изображений, к изучению и применению которого мы приступаем. Первоначально изложим суть этого метода.

П усть в некоторой области пространства , ограниченной поверхностью (в частном случае граница области может простираться до бесконечности), задано распределение зарядов (рис.1). Электрическое поле в выделенной области определяется однозначно, если

- задано распределение зарядов внутри этой области;

- задано распределение потенциала на границе области.

Заметим, что на границе области могут существовать заряды, однако даже при неизвестном их распределении, задание потенциала на границе однозначно определяет поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов на границе удается подобрать такое распределение зарядов вне рассматриваемой области, что для нового распределения оказываются выполненными граничные условия исходной задачи. В этом случае дополнительные заряды называются зарядами-изображениями. Поиск изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и имеет простое решение.

Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой причине уделяется серьезное внимание в курсе электродинамики.

В этом параграфе мы уделим основное внимание методам построения изображений и расчетам характеристик полей. Рассматривать алгоритмы построения полей нет необходимости, так как они полностью аналогичны, изученным ранее.

4.2.1 Заряд над бесконечной плоскостью.

Постановка задачи.

Точечный заряд находится на расстоянии от бесконечной плоской проводящей пластины. Построим картину силовых линий поля. Найдем: распределение поверхностной плотности индуцированных зарядов на платине; силу взаимодействия заряда и пластины; энергию взаимодействия заряда и пластины. Как изменится электрическое поле, если заряд находится над толстой пластиной, изготовленной из диэлектрика с проницаемостью .

Метод расчета и результаты.

Если пластина является проводящей, то ее потенциал постоянен, так как она простирается до бесконечности, то этот потенциал равен нулю. Таким образом, задача сводится к расчету поля в полупространстве, в котором находится точечный заряд, а на плоской границе потенциал равен нулю. Воспользуемся методом изображений.

П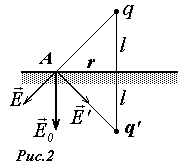 остроение заряда изображения в плоской проводящей пластине широко известно (рис.2). Достаточно расположить заряд-изображение равный по величине и противоположный по знаку исходному и симметрично ему и граничные условия ( на поверхности пластины будут выполнены). Следовательно, в верхнем полупространстве поле заряда и зарядов, индуцированных на поверхности пластины эквивалентно полю двух равных по величине и противоположных по знаку точечных зарядов и . В нижнем полупространстве поле отсутствует (действует электростатическая защита). Силовые линии такого поля мы уже рассчитывали, поэтому приводим итог без комментариев (рис.3).

О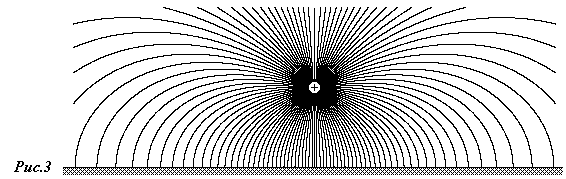 братите внимание, что силовые линии входят в пластину под прямым углом, как того и требуют условия равновесия зарядов на поверхности проводника. Интересно, но и понятно распределения потенциала в плоскости, содержащей заряд и перпендикулярной границе раздела сред. Уже знакомый нам резкий «холм» потенциала уединенного точечного потенциала оказывается, как бы прижатым с одной стороны, там, где бесконечная проводящая пластина прижимает его к нулю (рис.4).

Заметим, что распределение поверхностных зарядов создает в верхнем полупространстве такое же поле, как и поле точечного заряда . Ввиду явной симметрии такое же поле возникает и в нижней половине (то есть поле заряда , расположенного в той же точке, что и исходный заряд ). Это поле индуцированных зарядов складывается с полем исходного заряда, поэтому и оказывается, что в нижнем полупространстве поле равно нулю, как и должно быть внутри проводника.

Для расчета поверхностной плотности индуцированных зарядов на поверхности проводника воспользуемся известной формулой, связывающей с напряженностью поля у поверхности

. (1)

Напряженность поля у границы можно рассчитать по принципу суперпозиции как сумму полей, создаваемых исходным зарядом и его изображением (см. рис.2):

.

Суммарный вектор направлен перпендикулярно границе и равен

, (2)

здесь расстояние от основания перпендикуляра, опущенного из заряда на плоскость пластины, до рассматриваемой точки. Поверхностная плотность заряда у поверхности проводника связана с напряженностью поля соотношением , поэтому распределение поверхностной плотности индуцированных зарядов на пластине осесимметрично и имеет вид

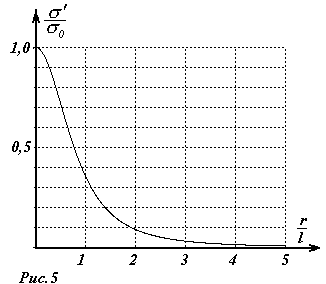, (3)

зависящий только от расстояния до основания перпендикуляра, график этой зависимости показан на рис.5. Величина - есть поверхностная плотность зарядов непосредственно под исходным зарядом.

Теоретически вся пластина заряжается, однако основная часть индуцированных зарядов появляется в круге радиус, которого в два раза больше расстояния от заряда до пластины.

Сила взаимодействия заряда и пластины равна силе взаимодействия зарядов и :

. (4)

Энергия взаимодействия равна половине (!) энергии взаимодействия зарядов и . Заметьте, что две задачи (заряд и пластина - два заряда) эквивалентны только в верхнем полупространстве. Реально поле существует только в верхней половине пространства. Так энергия взаимодействия есть энергия поля, то и энергия взаимодействия будет в два раза меньше. Поэтому

. (5)

Этот же результат для энергии взаимодействия получается, если вычислить энергию взаимодействия, как работу, которую необходимо совершить, чтобы унести заряд на бесконечность.

Еще одно интересное, на мой взгляд, пояснение, почему энергия взаимодействия уменьшается в два раза. При двух реальных точечных зарядах при перемещении одного из них второй остается неподвижным. Если же уносить заряд от проводящей границы, то его изображение также удаляется.

Рассмотрим, как изменится электрическое поле, если нижнюю часть пространства заполнить однородным диэлектриком с проницаемостью .

Расчет электрических полей в присутствии диэлектриков намного сложней, чем решение аналогичных задач для проводников. Математически это усложнение заключается в других граничных условиях. Так для проводников, находящихся в электростатическом поле выполняются условия: потенциал проводника постоянен; вектор напряженности поля у поверхности проводника перпендикулярен поверхности.

Н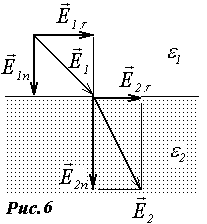 а границе диэлектриков при отсутствии на ней свободных зарядов выполняются условия (рис.6):

- тангенциальные составляющие векторов напряженности полей одинаковы

; (6)

- нормальные составляющие векторов напряженности претерпевают разрыв, такой, что выполняется соотношение

, (7)

где - диэлектрические проницаемости граничащих сред. Поверхностная плотность поляризационных зарядов на границе диэлектриков может быть найдена с помощью теоремы Гаусса и определяется по формуле

. (8)

Предположим¹, что на плоской границе диэлектрика, взаимодействующего с точечным зарядом , возникают поляризационные заряды, распределение которых совпадает с распределением зарядов на поверхности проводника, находящегося в аналогичных условиях (см. формулу (3)).

Такое распределение поверхностных зарядов, создает в полупространстве поле, эквивалентное полю точечного заряда.

Т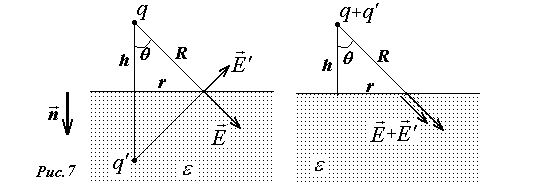 аким образом, будем рассматривать поле в верхнем полупространстве над диэлектриком как суперпозицию зарядов и , расположенных по разные стороны от границы, а поле внутри диэлектрика как поле двух точечных зарядов и , расположенных в одной точке.

Для того, чтобы доказать справедливость нашего предположения необходимо добиться выполнения граничных условий (6)-(7). Легко видеть (рис.7), что условие постоянства тангенциальной составляющей выполняется при любом значении заряда-изображения . Попытаемся подобрать такую величину этого заряда, что бы выполнялось граничное условие и для нормальных составляющих поля. Согласно нашему предположению, в пространстве над диэлектриком возле границы нормальная составляющая поля определяется формулой

, (9)

а внутри диэлектрика, непосредственно у границы

. (10)

Граничное условие (7) будет выполняться в любой точке границы, если положить

,

или

. (11)

Итак, мы показали, что предположение о характере распределения поляризационных зарядов на границе диэлектрика справедливо, так выполняются граничные условия. Величина поверхностной плотности зарядов вычисляется по формуле (3), применение которой в данном случае приводит к результату

. (12)

Силу, действующую на точечный заряд, можно вычислить как силу взаимодействия двух точечных зарядов и :

. (13)

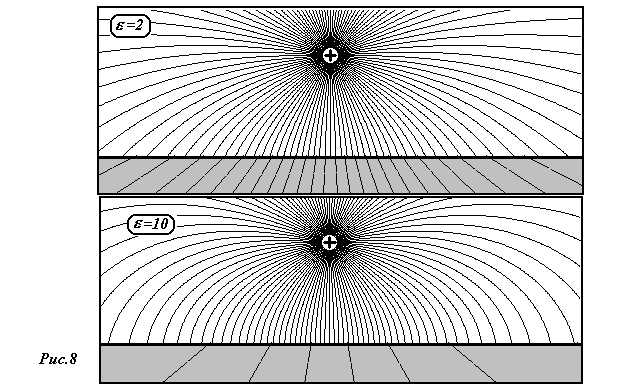
Теперь можно построить картину силовых линий поля: напомню, вне диэлектрика поле совпадает с полем двух точечных зарядов и , расположенных симметрично относительно границы раздела; а внутри диэлектрика совпадает с полем точечного заряда . На рис.8 показаны картины поля при разных значениях диэлектрической проницаемости. Обратите внимание, что при увеличении проницаемости, диэлектрик вносит все большие изменения в структуру поля.

Переход от диэлектрика к проводнику в задачах электростатики может быть осуществлен, полагая , действительно, в этом пределе формулы (12), (13) переходят в соответствующие формулы, полученные ранее для проводника. Если же положить , то все индуцированные заряды исчезают, как и должно быть в отсутствие диэлектрика.

Отметим особо, что поле внутри диэлектрика в данном случае совпадает с полем точечного заряда, величина которого равна . То есть диэлектрик уменьшает поле, но не в раз, как это бывает в случае бесконечного диэлектрика.