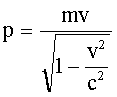Систематизирующая таблица по основным формулам раздела «Оптика и элементы квантовой физики »
Абсолютный показатель преломления где с - скорость света в вакууме, с=3·108 м/с, v - скорость распространения света в среде. |
|
|
Относительный показатель преломления где n2 и n1 - абсолютные показатели преломления второй и первой среды. |
|
|
Закон преломления где i - угол падения, r - угол преломления. |
|
|
Формула тонкой линзы где F - фокусное расстояние линзы, d - расстояние от предмета до линзы, f - расстояние от линзы до изображения. |
|
|
Оптическая сила линзы где R1 и R2 - радиусы кривизны сферических поверхностей линзы. Для выпуклой поверхности R>0. Для вогнутой поверхности R<0. |
|
|
Оптическая длина пути: где n - показатель преломления среды; r - геометрическая длина пути световой волны. |
|
|
Оптическая разность хода:
|
|
|
Условие интерференционного максимума: минимума: где λ0 - длина световой волны в вакууме; m - порядок интерференционного максимума или минимума. |
|
|
Оптическая разность хода в тонких пленках в отраженном свете: в проходящем свете: где d - толщина пленки; i - угол падения света; n - показатель преломления. |
|
|
Ширина интерференционных полос в опыте Юнга: где d - расстояние между когерентными источниками света; L - расстояние от источника до экрана. |
|
|
Условие главных максимумов дифракционной решетки: где d - постоянная дифракционной решетки; φ - угол дифракции. |
|
|
Разрешающая способность дифракционной решетки: где Δλ - минимальная разность длин волн двух спектральных линий, разрешаемых решеткой; m - порядок спектра; N - общее число щелей решетки. |
|
|
Закон Малюса: где I0 - интенсивность плоско-поляризованного света, падающего на анализатор; I - интенсивность света, прошедшего через анализатор; α - угол между плоскостью поляризации падающего света и главной плоскостью анализатора. |
|
|
Связь интенсивности естественного света Iест с интенсивностью света, прошедшего поляризатор (и падающего на анализатор): где k - относительная потеря интенсивности света в поляризаторе. |
|
|
Дисперсия вещества |
|
|
Средняя дисперсия |
|
|
Групповая скорость света |
|
|
Фазовая скорость света |
|
|
Закон Стефана-Больцмана: где R - энергетическая светимость (излучательность) абсолютно черного тела, т.е. энергия, испускаемая в единицу времени с единицы площади: σ - постоянная Стефана-Больцмана: |
|
|
Закон смещения Вина: где λm - длина волны, на которую приходится максимум энергии излучения; b - постоянная Вина : |
|
|
Импульс фотона: где λ - длина волны; h - постоянная Планка: |
|
|
Энергия фотона: где ν - частота; с - скорость света в вакууме: |
|
|
Формула Эйнштейна для фотоэффекта:
где
hν - энергия фотона, падающего на
поверхность металла;
А - работа
выхода электрона из металла;
|
|
|
Красная граница фотоэффекта: где λк - максимальная длина волны, при которой возможен фотоэффект; νк - минимальная частота, при которой возможен фотоэффект. |
|
|
Сериальные формулы спектра водородоподобного атома где R - постоянная Ридберга R=1,097·107 м-1, z - порядковый номер элемента; Серия Лаймана m=1, n=2,3,4... Серия Бальмера m=2, n=3,4,5... Серия Пашена m=3, n=4,5,6... Серия Брекета m=4, n=5,6,7... и т.д. |
|
|
Длина волны де Бройля:
где р -
импульс частицы.
В классическом
приближении (при v<<c): p = mv;
m -
масса частицы;
v - скорость частицы;
с - скорость света в вакууме.
В
релятивистском случае (при
|
|
|
Связь импульса с кинетической энергией Wк в релятивистском приближении: где E0 - энергия покоя частицы: |
|
|
Плотность вероятности нахождения частицы в соответствующем месте пространства |
|
|
Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме где l - ширина ямы, х - координата частицы в яме (0 ≤ x ≤ l), n - квантовое число (n=1,2,3...). |
|
|
Энергия частицы в бесконечно глубокой одномерной потенциальной яме где m - масса частицы. |
|
|
-
оптические пути двух световых волн.
-
максимальная кинетическая энергия
фотоэлектрона.
или
):
