Graph 3 – Agilent Technologies squared returns
Ratio Analysis
We
find outliers in the returns by using the formula
.
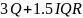The 3rd
quartile represents an observation which is larger than three
quarters of all of the observations. The IQR (Inter-Quartile range)
is the difference between the third quartile and the first quartile,
where the 1st
quartile represents an observation which is larger than one quarter
of all of the observations. If the adjusted company A’s return
satisfies the following inequality, it is considered an outlier:
We
only look for outliers on the upper side (not
),
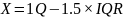because all of our returns are squared and therefore nonnegative,
while the lower critical value of X is below 0. For all of the stocks
the number of days is 503, representing two trading years. Out of
these days, there are approximately 50±5 outliers for different
companies. These outliers represent a significant difference in the
returns between the stock and the S&P 500 index.
To see, whether the competitors’ stock prices are affected I am going to do the following tests:
First is to see, whether a significant return in company A’s stock causes a significant opposite return in the competitors’ stock prices. To do so, I first identify the outliers for company A and its competitors. Then, I check, if outliers of both companies coincide, which we call co-reactions. Finally, I check whether the outliers have opposite signs. The number of these events is calculated and divided by the number of outliers in the returns of company A, which provides us with the ratio RN (standing for co-Reactions Negative). The proportion is tested against the null hypothesis of being less or equal to the Opposite Ratio (OR). The opposite ratio is the number of times the company A had opposite returns with its competitors over the total number of observations. If the RN ratio is higher than the OR ratio we can say that significant news on average has a significant opposite effect on the competitors’ share prices.
Secondly; I am going to check if a significant return for company A causes a general opposite return in the competitors’ stock (not necessarily significant). This means checking if an outlier in the company A’s returns coincides with an opposite return in the competitors’ stocks on the same day. The number of such events is calculated, divided by the total number of outliers in company A’s return and named Neg (Negative ratio). The Neg ratio is then tested against the null hypothesis of being less or equal to the Opposite Ratio. If the null hypothesis is rejected we can conclude that significant news for company A has some opposite effect on the competitors’ share prices.
This test is run because the first test did not show significant opposite effect on competitors. So the goal is to check whether there is any negative effect at all.
The
table below shows the how adjusted returns are calculated. The
control returns are subtracted from the Initial returns, which gives
the adjusted returns. For Agilent Technologies (US:A), the adjuster
returns are:
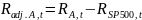. The same process is done for Teradyne (US:TER) and Thermo Fisher
Scientific (TMO). Then the adjusted returns are squared and outliers
are located. The “Outlier Test” part of the table checks if the
return at time t
fits the outlier inequality. If that is the case “TRUE” value is
displayed.
Date |
Initial Returns |
|
Control |
|
Adjusted Returns |
|
Outlier Test |
||||||||||||
A |
TER |
TMO |
SP500 |
A |
TER |
TMO |
|
A |
TER |
TMO |
|||||||||
|
|
|
|
|
|
|
|
OUTLIER? |
OUTLIER? |
OUTLIER? |
|||||||||
28/11/2011 |
3.90% |
3.60% |
2.60% |
2.88% |
0.97% |
0.73% |
-0.26% |
|
0 |
0 |
0 |
||||||||
29/11/2011 |
-0.40% |
-0.20% |
1.10% |
0.22% |
-0.62% |
-0.47% |
0.85% |
|
0 |
0 |
0 |
||||||||
30/11/2011 |
6.80% |
10.80% |
2.50% |
4.24% |
2.60% |
6.58% |
-1.75% |
|
TRUE |
TRUE |
TRUE |
||||||||
01/12/2011 |
0.80% |
-0.70% |
-0.40% |
-0.19% |
1.04% |
-0.48% |
-0.25% |
|
0 |
0 |
0 |
||||||||
02/12/2011 |
-2.80% |
-1.60% |
-1.10% |
-0.02% |
-2.82% |
-1.56% |
-1.04% |
|
TRUE |
0 |
0 |
||||||||
05/12/2011 |
0.80% |
2.50% |
0.50% |
1.02% |
-0.21% |
1.45% |
-0.51% |
|
0 |
0 |
0 |
||||||||
06/12/2011 |
-0.20% |
0.90% |
0.90% |
0.11% |
-0.33% |
0.78% |
0.74% |
|
0 |
0 |
0 |
||||||||
07/12/2011 |
-0.90% |
0.10% |
-0.40% |
0.20% |
-1.07% |
-0.05% |
-0.63% |
|
0 |
0 |
0 |
||||||||
08/12/2011 |
-6.30% |
-1.90% |
-3.70% |
-2.14% |
-4.17% |
0.29% |
-1.53% |
|
TRUE |
0 |
TRUE |
||||||||
09/12/2011 |
2.60% |
5.40% |
0.80% |
1.67% |
0.94% |
3.71% |
-0.90% |
|
0 |
TRUE |
0 |
||||||||
12/12/2011 |
-4.60% |
-2.90% |
-1.10% |
-1.50% |
-3.13% |
-1.37% |
0.38% |
|
TRUE |
0 |
0 |
||||||||
13/12/2011 |
-1.70% |
-3.40% |
-1.00% |
-0.87% |
-0.86% |
-2.54% |
-0.11% |
|
0 |
TRUE |
0 |
||||||||
14/12/2011 |
-0.70% |
-2.90% |
-2.10% |
-1.14% |
0.48% |
-1.77% |
-0.98% |
|
0 |
0 |
0 |
||||||||
15/12/2011 |
1.60% |
-0.10% |
0.90% |
0.32% |
1.24% |
-0.40% |
0.59% |
|
0 |
0 |
0 |
||||||||
16/12/2011 |
0.00% |
2.50% |
-0.70% |
0.32% |
-0.29% |
2.21% |
-1.03% |
|
0 |
0 |
0 |
||||||||
19/12/2011 |
-0.70% |
-3.00% |
-0.70% |
-1.18% |
0.49% |
-1.82% |
0.49% |
|
0 |
0 |
0 |
||||||||
20/12/2011 |
4.00% |
5.70% |
3.10% |
2.94% |
1.04% |
2.75% |
0.20% |
|
0 |
TRUE |
0 |
||||||||
21/12/2011 |
-0.60% |
-1.00% |
-0.60% |
0.19% |
-0.83% |
-1.23% |
-0.80% |
|
0 |
0 |
0 |
||||||||
Table
3 – Testing
returns for abnormal volatility, denoted as “outliers”
A
– Agilent Technologies, TER – Teradyne, TMO – Thermo Fisher
Scientific
SP500 – Standard & Poor 500
For the first test we only look for cases, when company A’s outliers coincide with its competitors’ outliers. Therefore we filter and leave only “true” values for the company (Agilent Technologies, A). However, a case when there are two outliers does not mean that a significant return of Agilent Technologies led to a significant opposite return for its competitors. As we can see, on the 8th of December Agilent Technologies and Thermo Fisher Scientific both had significant negative returns and therefore we cannot use that day for our first test. To satisfy the first test we need two things to be true: there are significant returns for 2 (or three) companies AND the returns are opposite for the company A and its competitors.
The “Reaction?” table checks whether the values of “TRUE” coincide for A-TER (Agilent Technologies and Teradyne) and for A-TMO (Agilent Technologies and Thermo Fisher Scientific). In other words it checks if outliers happen on the same day for two companies. The “Opposite?” table checks whether the returns for the pair of stock are of opposite sign. Finally the “R and N” table checks if both the “Reaction?” and “Opposite?” tables say “Yes”, that is if a significant return for Agilent Technologies coincides with a significant opposite return of its competitor.
Date |
Opposite test |
|
Outlier test |
|
co-Reaction test |
|
RN test |
|||||||||||
A-TER |
A-TMO |
A |
TER |
TMO |
|
A-TER |
A-TMO |
|
A-TER |
A-TMO |
||||||||
Opposite? |
Opposite? |
Outlier? |
Outlier? |
Outlier? |
|
Reaction? |
Reaction? |
|
R and N |
R and N |
||||||||
30/11/2011 |
0 |
1 |
TRUE |
TRUE |
TRUE |
|
1 |
1 |
|
0 |
1 |
|||||||
02/12/2011 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
08/12/2011 |
1 |
0 |
TRUE |
0 |
TRUE |
|
0 |
1 |
|
0 |
0 |
|||||||
12/12/2011 |
0 |
1 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
28/12/2011 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
1 |
|
0 |
0 |
|||||||
03/01/2012 |
1 |
0 |
TRUE |
0 |
TRUE |
|
0 |
1 |
|
0 |
0 |
|||||||
09/01/2012 |
0 |
1 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
17/01/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
18/01/2012 |
0 |
0 |
TRUE |
TRUE |
TRUE |
|
1 |
1 |
|
0 |
0 |
|||||||
20/01/2012 |
1 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
24/01/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
25/01/2012 |
1 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
26/01/2012 |
1 |
0 |
TRUE |
TRUE |
TRUE |
|
1 |
1 |
|
1 |
0 |
|||||||
01/02/2012 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
1 |
|
0 |
0 |
|||||||
03/02/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
07/03/2012 |
0 |
1 |
TRUE |
TRUE |
0 |
|
1 |
0 |
|
0 |
0 |
|||||||
12/03/2012 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
1 |
|
0 |
0 |
|||||||
05/04/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|
0 |
0 |
|||||||
Table
4 – Testing
for opposite co-Reactions
A
– Agilent Technologies, TER – Teradyne, TMO – Thermo Fisher
Scientific
SP500 – Standard & Poor 500
Then I do the second test, which checks if a significant return in the stock A happens with a general opposite (not necessarily significant) return in the competitors’ stock. Table “Neg” checks if an outlier in Agilent Technologies’ adjusted returns coincides with an opposite return in competitor’s stock.
Date |
Opposite test |
|
Outlier test |
|
Negative test |
||||||||
A-TER |
A-TMO |
A |
TER |
TMO |
|
A-TER |
A-TMO |
||||||
Opposite? |
Opposite? |
Outlier? |
Outlier? |
Outlier? |
|
NEG |
NEG |
||||||
30/11/2011 |
0 |
1 |
TRUE |
TRUE |
TRUE |
|
0 |
1 |
|||||
02/12/2011 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|||||
08/12/2011 |
1 |
0 |
TRUE |
0 |
TRUE |
|
1 |
0 |
|||||
12/12/2011 |
0 |
1 |
TRUE |
0 |
0 |
|
0 |
1 |
|||||
28/12/2011 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
0 |
|||||
03/01/2012 |
1 |
0 |
TRUE |
0 |
TRUE |
|
1 |
0 |
|||||
09/01/2012 |
0 |
1 |
TRUE |
0 |
0 |
|
0 |
1 |
|||||
17/01/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|||||
18/01/2012 |
0 |
0 |
TRUE |
TRUE |
TRUE |
|
0 |
0 |
|||||
20/01/2012 |
1 |
0 |
TRUE |
0 |
0 |
|
1 |
0 |
|||||
24/01/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|||||
25/01/2012 |
1 |
0 |
TRUE |
0 |
0 |
|
1 |
0 |
|||||
26/01/2012 |
1 |
0 |
TRUE |
TRUE |
TRUE |
|
1 |
0 |
|||||
01/02/2012 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
0 |
|||||
03/02/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|||||
07/03/2012 |
0 |
1 |
TRUE |
TRUE |
0 |
|
0 |
1 |
|||||
12/03/2012 |
0 |
0 |
TRUE |
0 |
TRUE |
|
0 |
0 |
|||||
05/04/2012 |
0 |
0 |
TRUE |
0 |
0 |
|
0 |
0 |
|||||
Table
5 – Testing
for opposite returns given significant returns for Agilent
Technologies
A
– Agilent Technologies, TER – Teradyne, TMO – Thermo Fisher
Scientific
SP500 – Standard & Poor 500
The process is continued with all other 28 companies. Then the following ratios are calculated: 1) {the number of times a significant return for company A caused a significant opposite return to its competitors} over {the total number of significant returns for company A} = (Ratio RN) and 2) {the number of times a significant return for company A caused an opposite (not necessarily significant) return to its competitors} over {the total number of significant returns for company A} = (Ratio Neg) 3) {the number of times the company A had opposite returns with its competitors} over {the total number of returns} (Opposite Ratio, OR).
To see if news affect both company A and its competitor we have to compare the ratios RN and Neg with overall “opposite ratio”. If the news do affect both company A and its competitors, then the ratio RN and/or ratio Neg have to be significantly larger than the opposite ratio.
Significant opposite reaction test
H0: news that significantly affects company A does not have a significant opposite effect on its competitors. RN < OR
Ha: news that significantly affects company A has a significant opposite effect on its competitors. RN > OR
Opposite reaction test
H0: news that significantly affects company A does not have an opposite effect on its competitors
Ha: news that significantly affects company A has an opposite effect on its competitors
|
Competitor 1 |
|
Competitor 2 |
||||
|
OR |
RN |
Neg |
OR |
RN |
Neg |
|
A |
38.57% |
4.08% |
28.57% |
39.76% |
6.12% |
26.53% |
|
AAPL |
45.33% |
5.26% |
54.39%* |
50.70% |
1.75% |
29.82% |
|
ADI |
32.60% |
0.00% |
3.70% |
|
|
|
|
ALTR |
27.83% |
1.82% |
14.55% |
|
|
|
|
AMAT |
31.81% |
0.00% |
10.71% |
|
|
|
|
AMD |
41.35% |
10.00% |
30.00% |
53.48% |
8.00% |
52.00% |
|
BRCM |
40.76% |
3.28% |
26.23% |
35.98% |
3.28% |
27.87% |
|
CIEN |
41.95% |
0.00% |
25.49% |
|
|
|
|
CSCO |
41.95% |
0.00% |
33.33% |
48.71% |
1.85% |
38.89% |
|
EMC |
49.30% |
5.56% |
55.56% |
43.94% |
1.85% |
20.37% |
|
GOOG |
42.54% |
6.82% |
36.36% |
45.33% |
2.27% |
40.91% |
|
HPQ |
45.13% |
1.85% |
38.89% |
|
|
|
|
IBM |
45.13% |
1.96% |
41.18% |
48.71% |
5.88% |
43.14% |
|
INTC |
41.35% |
9.80% |
41.18% |
43.94% |
0.00% |
43.14% |
|
KLAC |
31.81% |
0.00% |
20.83% |
|
|
|
|
LLTC |
29.03% |
0.00% |
5.36% |
30.22% |
0.00% |
10.71% |
|
LXK |
45.33% |
3.08% |
55.38%* |
|
|
|
|
MSFT |
46.72% |
5.77% |
59.62%** |
48.71% |
5.77% |
51.92% |
|
MXIM |
36.78% |
2.44% |
12.20% |
35.19% |
2.44% |
14.63% |
|
NCR |
50.10% |
8.70% |
47.83% |
49.50% |
6.52% |
47.83% |
|
NTAP |
43.54% |
5.00% |
30.00% |
37.57% |
1.67% |
30.00% |
|
QCOM |
43.94% |
0.00% |
33.93% |
|
|
|
|
QLGC |
43.74% |
3.85% |
36.54% |
45.13% |
1.92% |
48.08% |
|
SATM |
34.59% |
5.26% |
29.82% |
|
|
|
|
TMO |
39.76% |
5.56% |
20.37% |
|
|
|
|
TXN |
38.97% |
0.00% |
25.93% |
|
|
|
|
XLNX |
27.83% |
1.64% |
9.84% |
|
|
|
|
XRX |
44.73% |
7.02% |
28.07% |
|
|
|
|
YHOO |
46.52% |
0.00% |
34.00% |
45.33% |
2.00% |
40.00% |
|
Table
6 – Results
|| Comparing
RN and Neg Ratios to the Opposite Ratio
*
- significantly larger at 90% confidence level
**
- significantly larger at 95% confidence level
