12. Несмещенность

Оценка ^θ(х₁..х_n) называется несмещенной, если

Несмещенная оценка – это такая оценка, среднее значение которой совпадает с истинным значением измеряемого параметра.

12. Эффективность

Оценка называется эффективной, если она:

1. Несмещенная

2. Имеет минимально возможную дисперсию (при подстановке в неравенство Рао-Крамера оно переходит в равенство):

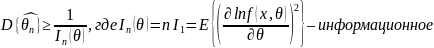
12. Асимптотические свойства

Оценка ^θ(x₁..x_n) называется состоятельной, если

Оценка ^θ называется асимптотически несмещенной, если

Оценка ^θ называется асимптотически эффективной, если ее асимптотическая дисперсия минимально возможна (или неравенство Рао-Крамера выполняется в асимптотике). Оценка асимптотически эффективна, если ее эффективность по отношению к любой эффективной оценке =1:

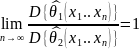
Оценка асимптотически нормальна, если для нее выполняется центральная предельная теорема, т.е. ее распределение асимптотически нормально.

12. Доверительные интервалы

Точечные оценки дают приближенное значение неизвестного параметра. Если известен закон распределения оценки или ее дисперсия, то можно указать пределы, в которых с большой вероятностью находится неизвестное значение параметра.

Интервал называют доверительным, если он покрывает неизвестный параметр с заданной надежностью: 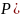θ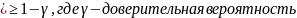

Граничные точки доверительного интервала называют доверительными пределами.