12. Основные понятия мат.Статистики

(X, A, P) – статистическая структура, основное понятие мат.статистики

X – выборочное пространство, множество всех возможных результатов наблюдения

A – G-алгебра

P , где F(x,0) – функция распределения изучаемой случайной величины Х.

Статистика – любая измеримая функция наблюдений.

12. Повторная выборка

Выборка x₁…x_n – набор из n результатов эксперимента над случайной величиной Х.

Выборка x₁…x_n называется повторной, если :

1. Все элементы выборки одинаково распределены (имеют один и тот же распределительный закон): F(x_i) = F(x_j), i≠j

2. x_i, x_j – независимы при i≠j.

12. Частотный способ задания вероятности

В наборе фиксированных условий с вероятностью р происходит событие A (все испытания независимы). Тогда 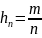, где n – количество всех проведенных испытаний, m – испытания, результатом которых стало наступление события А. Отсюда вероятность наступления события A выражается как для любой непредвзято выбранной последовательности.

Частота может рассматриваться как случайная величина H_n(A).

12. Закон больших чисел

Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.

Пусть есть бесконечная последовательность одинаково распределенных и некоррелированных случайных величин определенных на одном вероятностном пространстве : .

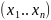- выборочное среднее.

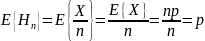, если

Закон больших чисел: , т.е.

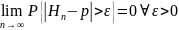
12. Теорема Муавра-Лапласа

Если при каждом из n независимых испытаний вероятность появления некоторого случайного события равна р (0<р<1) и m — число испытаний, в которых это событие фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Пусть

Тогда

Если

,

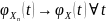
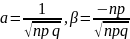
12. Оценка числа необходимых наблюдений

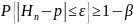(1)

Требуется оценить n при любых ε, β, p

1. Приведем неравенство (1) к теореме Муавра-Лапласа:

2. 

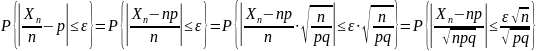
При заданном β корнем уравнения является

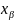
Если x> , то верно неравенство

3. =>

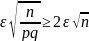
Следовательно, если неравенство 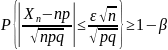решается для , то оно будет выполняться и для => =>

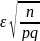12. Усиленный закон больших чисел

Пусть есть бесконечная последовательность одинаково распределенных и некоррелированных случайных величин определенных на одном вероятностном пространстве : .

- выборочное среднее.

, если

Усиленный закон больших чисел: 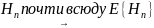, т.е.

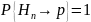
12. Вспомогательная случайная величина ^Х

Для случайной величины Х, распределение которой неизвестно, задается вспомогательная случайная величина ^Х:

х⁽¹⁾ – наименьший элемент выборки,

х⁽²⁾ – наименьший элемент из оставшихся и т.д.

Каждому такому элементу ставится в соответствие вероятность р=m_i/n, где m_i – число раз, с которым х⁽ⁱ⁾ встречается в исходной выборке.

^F_X(x) – эмпирическая функция распределения исходной величины Х (рисуется ступеньками).

12. Выборочные аналоги

Распределение случайной величины Х неизвестно. ^X-характеристики = выборочные аналоги Х.

– функция наблюдений(выборочное среднее).

- выборочная дисперсия

Выборочный аналог плотности – гистограмма:

12. Центральная предельная теорема

Если x₁…x_n одинаково распределены и независимы, и для каждого из них существует мат.ожидание E{x_i}=а и дисперсия D{x_i}=G², то для них справедливо:

Д-о: Разложим характеристическую функцию величин x_i-a по формуле:

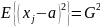
Тогда .

12. Метод моментов

Если функция распределения зависит от s параметров , то выборочные моменты 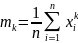являются функциями от параметров .

…

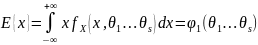
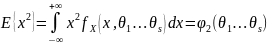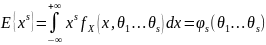
Если данную систему можно разрешить относительно 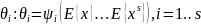, то получаем оценку неизвестных параметров θ.

12. Оценки максимального правдоподобия

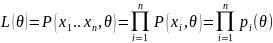- функция максимального правдоподобия (если Х – дискретная случайная величина)

Θ* - оценка максимального правдоподобия θ,

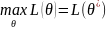
Поскольку lnL при фиксированных x₁..x_n достигает максимума при том же значении θ, что и L, для нахождения оценки можно решить уравнение правдоподобия

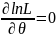
Каждое решение уравнения правдоподобия, зависящее от x₁..x_n – оценка наибольшего правдоподобия для θ.