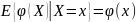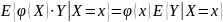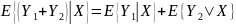Характеристическая функция и ее свойства
Характеристическая функция – способ задания распределения комплекснозначной случайной величины.
ϕ(t) – характеристическая функция
Свойства:
Для любой случайной величины существует единственная характеристическая функция. Пусть X, Y - две случайные величины, и
.
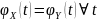Тогда P(X)=P(Y).
В частности, если обе величины абсолютно
непрерывны, то совпадение характеристических
функций влечёт совпадение плотностей.
Если обе случайные величины дискретны,
то совпадение характеристических
функций влечёт совпадение функций
вероятности.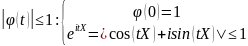
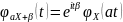
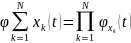
11) Независимость и некоррелированность
Случайные величины называются некоррелированными, если Cov(x,y)=0. Из независимости следует некоррелированность, но не наоборот.
Условное математическое ожидание случайной величины и его свойства.
Условное
мат.ожидание:
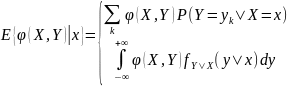-среднее значение величины Y
при условии, что X=x.
Условное математическое ожидание — это случайная величина, а не число!
Свойства:
Д-о:
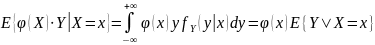
Д-о:
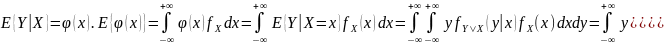
Регрессия. Уравнение линейной регрессии
Регрессия
случайной величины - зависимость
среднего значения какой-либо случайной
величины от некоторой другой величины
.
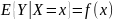Если
,
то говорят, что между случайными
величинами существует регрессионная
связь. Если X,
Y
– независимы, то E{Y|X}
= E{Y}:
,
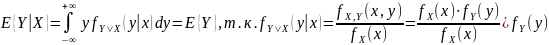
коэффициенты
подбираются с помощью метода наимен6ьших
квадратов:
Пусть X, Y – произвольные случайные величины, Y=aX+b.
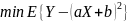– метод наименьших
квадратов для линейной функции.
Производящая функция нормального распределения
Нормальное распределение, также называемое распределением Гаусса, —распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений, в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий. Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть, является, с математической точки зрения, не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Плотность
вероятности нормально
распределённой случайной величины с
параметром смещения a и
масштаба G имеет
следующий вид:
.
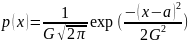Функция
распределения такой величины не
выражается через элементарные функции
и записывается по определению
через интеграл Римана как
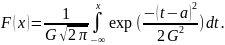
Характеристическая
функция нормального распределения
имеет вид
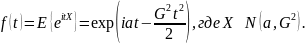
Производящая
функция моментов Х определена
для всех вещественных t:
Класс задач мат.Статистики
О математической статистике имеет смысл вспоминать, если
имеется случайный эксперимент, свойства которого частично или полностью неизвестны,
мы умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое (а лучше — какое угодно) число раз.
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
Различают два класса задач: оценка параметра и различение гипотез.