1. Определение моментов случайной величины

Моментом k-го порядка распределения случайной величины Х точки а называется: ν_k(а)=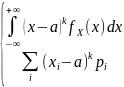

Моментом порядка k функции случайной величины 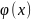называется: ν_k(а)=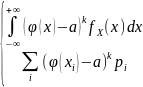

Моментом порядка k относительно точки а функции 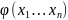называется: ν_k(а)=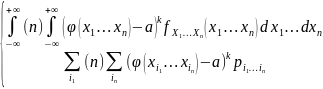

Если а=0, то соответствующий момент называется начальным. Среди всех моментов первого порядка который называется мат.ожиданием.

2. Математическое ожидание и его свойства

Математическим ожиданием случайной величины Х называется начальный момент первого порядка:

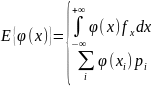
Математическим ожиданием функции 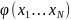называется:

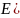
Свойства мат.ожидания:

• E{C} = C;

• E{CX} = C*E{X};

• E{aX+b} = a*E{X}+b;

• E{ } = ;

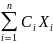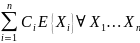• E{X₁,X₂} = E{X₁}*E{X₂}, если Х₁, Х₂ – независимые

Если а=Е{X}, то моменты называются центральными (E{X} – число!). Среди всех центральных моментов выделяется момент 2-го порядка, называемый дисперсией.

3. Дисперсия и ее свойства

Дисперсией называется мат.ожидание, определенное как:

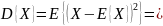
Дисперсия служит мерой степени разброса значений случайной величины около ее математического ожидания. Величина 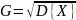называется средним квадратическим отклонением.

Свойства дисперсии:

• D{C} = 0 => D{X} = 0  X=const почти всюду

Д-о: 1.

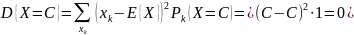
2. D{X} = 0 => X=x_k=E{X} => P(X=E{X})=1 => X=E{X}=C

• D{CX} = C²*D{X}

• D{X+Y} = D{X}+D{Y}, если Х, У – независимы

Д-о:

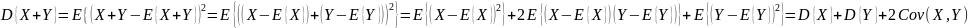
• Если Х₁..X_N – независимы, тогда

• 

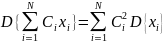
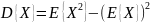
• Среди всех моментов второго порядка дисперсия минимальна

4. Математическое ожидание и дисперсия биномиальной случайной величины

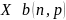
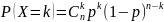
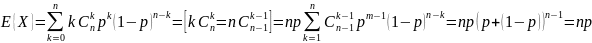
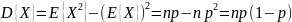
5. Неравенство Чебышева и следствия

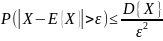, ε>0

Д-о:

Х – непр.

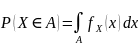
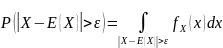
В области интегрирования |X-E{X}|/ε>1, тогда

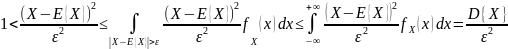
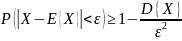
Следствия из неравенства Чебышева:

1. 

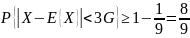
2. Закон больших чисел

6. Смешанные моменты

Пусть задан случайный вектор 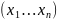. Смешанным моментом порядка k называется 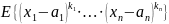, где

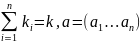
Если а=(0,0….0), то момент начальный

Если 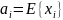, то соответствующий момент – центральный

7. Ковариация и ее свойства

Смешанным моментом порядка k называется мат.ожидани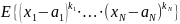е , где 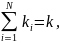a=(a₁,..,a_N).

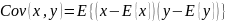
Ковариация – характеристика степени линейной вероятностной связи.

• Cov(x,x)=D(x)

• Cov(αx_i+β,γx_j+δ) = αγCov(x_i,x_j)

• Cov(x_i,x_j) = E{x_i*x_j} – E{x_i}*E{x_j}

• Если x_i, x_j независимы, то Cov(x_i,x_j)=0

Справедливо, => из п.(3), т.к. E{x_i*x_j} = E{x_i}*E{x_j}

• D{x_i+x_j} =D{x_i}+D{x_j}+2 Cov(x_i,x_j)

• 

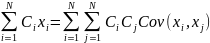
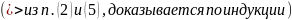
• Gij = Cov(x_i,x_j)

|| Gij|| - ковариантная матрица, является неотрицательно определенной

8. Коэффициент корреляции и его свойство

Коэффициентом корреляции называется

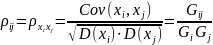
Свойства:

• 

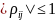
• Если xi, xj независимы, то

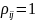
• (Y=aX+b) 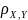 (| |=1)

9. Производящая функция моментов

Пусть есть случайная величина Х с распределением Р. Тогда её производящей функцией моментов называется функция, имеющая вид: 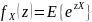, где z – комплексная переменная.

Раскладывая по Тейлору: