2. По характеру искажений (свойствам изображения);

• равноугольные, -равновеликие ,-произвольные.

В равноугольных сохраняется подобие бесконечно малых фигур, масштаб длин не зависит от направления т = n= а = b = μ и отсутствует искажение углов ω = 0; масштаб площади равен квадрату масштаба длин

Условия равноугольности : f = 0; m = n, или для поверхности эллипсоида

а для поверхности сфероида радиуса R формулы сохраняются, но в них радиусы кривизны M и N заменяются на R, а радиус параллели r принимается равным R cosφ, и тогда

При изображении в равноугольных проекциях участков конечных размеров изменение частных масштабов длин обусловливает искажение контуров участков. В этих проекциях обычно сильно искажаются площади.

В равновеликих проекциях сохраняется постоянным отношение площадей на картографируемой поверхности и на плоскости. Постоянство отношения площадей распространяется не только на бесконечно малые участки, но и на участки конечных размеров.

В этих проекциях частный масштаб площадей

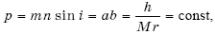
но чаще всего р= 1, поэтому условие равновеликости имеет вид h = Mr, а для поверхности шара

Экстремальные масштабы длин обратно пропорциональны друг другу

Максимальное искажение углов целесообразно вычислять по формулам тангенсов, которые в равновеликих проекциях принимают вид

В этих проекциях за счет искажения углов сильно искажаются контуры.

В произвольных не выполняются ни условия равноугольности, ни условия равновеликости, т. е. в них искажаются и углы и площади.

Среди произвольных проекций выделяют проекции равнопромежуточные,в которых сохраняется масштаб длин по одному из главных направлений а=1или b=1

Для вычислений максимального искажения углов рекомендуется использовать общую формулу

(1.64)

Для проекций с ортогональной сеткой аналогично выделяют равнопромежуточные проекции вдоль меридианов или вдоль параллелей, в которых соответственно частные масштабы длин равны т = 1 или п= 1.

3.По виду нормальной картографической сетки изображений меридианов и параллелей;

– цилиндрические, – конические, – азимутальные (перспективные),

–псевдоцилиндрические,– псевдоконические, – псевдоазимутальные,

– поликонические, – круговые, – производные (условные).

В цилиндрических меридианы – параллельные прямые, находящихся на равных расстояниях, пропорциональных разностям долгот, а параллели –

перпендикулярные меридианам параллельные прямые, отстоящие друг от друга на расстояниях, зависящих от свойств проекции.

В конических меридианы – прямые линии, сходящиеся под углами, пропорциональными разностям долгот; параллели – дуги концентрических окружностей с центром в точке схода меридианов.

В азимутальных меридианы – прямые линии, сходящиеся под углами равными разностям соответствующих долгот, а параллели – концентрические окружности с центром в точке пересечения меридианов. Перспективные - в которых поверхность Земли или других небесных тел отображается прямолинейными визирными лучами из точек пространства(точек зрения), на развертывающиеся поверхности цилиндра, конуса или на плоскость. Последние называют перспективными азимутальными проекциями.

В псевдоцилиндрических параллели – параллельные прямые линии, а меридианы – кривые, симметричные относительно среднего прямолинейного меридиана.

В псевдоконических параллели – дуги концентрических окружностей, а меридианы – кривые, симметричные относительно среднего – прямолинейного меридиана.

В псевдоазимутальных параллели – концентрические окружности, а меридианы – кривые, за исключением двух взаимноперпендикулярных меридианов, которые служат осями симметрии.

В поликонических меридианы – кривые, симметричные относительно среднего прямолинейного меридиана и экватора, а параллели – дуги эксцентрических окружностей, центры которых находятся на осевом меридиане.

В круговых и меридианы и параллели изображаются дугами эксцентрических окружностей.

Условные – проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий.

Многогранные– проекции, получаемые путем проектирования на поверхность многогранника, касательного или секущего шар (эллипсоид). Разновидностью многогранных проекций являются многополосные проекции, причем полосы могут нарезаться и по меридианам, и по параллелям. Такие проекции выгодны тем, что искажения в пределах каждой грани или полосы невелики, поэтому их всегда используют для многолистных карт.Многогранная проекция Мюфлинга действовала в России до начала 20 века

Проекция Гауса-Крюгера является равноугольной поперечной цилиндрической. В 1816 – 1820 гг. Гаусс занимался вопросами равноугольного изображения сфероида на плоскости. Он предложил но не опубликовал. Подробные исследования данной проекции были выполнены Л. Крюгером в 1912 и 1919 гг., который предложил способ непосредственного отображения эллипсоида на плоскости , т. е. дал рабочие формулы проекции. С тех пор проекция стала называться проекцией Гаусса – Крюгера.

В проекции Гаусса – Крюгера поверхность земли делят по меридианным зонам в шесть градусов по долготе, причем эти зоны приурочиваются к колоннам международной разграфки, положенной в основу номенклатуры Международной карты 1:1000 000.Каждая зона проектируется на поверхность своего цилиндра,касающегося шара по среднему (осевому) меридиану зоны.зоны нумеруются арабскими цифрами от гринвича.

Деление на зоны вызвано тем, что при большом удалении от осевого меридиана очень большие искажения в этой точке на карте.

В данной проекции меридианы и параллели изображаются кривыми, при этом меридианы симметричны относительно осевого, который по условию изображается прямой линией; параллели же симметричны относительно экватора, который изображается также прямой, т. е. проекция определяется тремя условиями: она симметрична относительно среднего меридиана и экватора, равноугольна, и сохраняет длины на среднем меридиане.

На плоскости в проекции Гауса применяется прямоуг.сист.координат,причем в каждой зоне своя.ось абсцисс-осевой,ординат-экватор.

Расстояния x,y-координаты Гауса.что бы ординаты были положительные к ним прибавляют 500 км.впереди ординаты пишут номер зоны.

Долгота осевого меридиана