Билет 14

1. Характеристика крупномасштабных планов. Точность, детальность и полнота планов

- планы, состав­ленные в масштабе 1:5000- 1:500.

По назначению планы подразделяются на 3 группы:

1. Основные, созданные с целью картографирования территории;

2. Специализированные планы: кадастровые, лесоустроительные, ру­словые, инженерно-топографические, землеустроительные;

3. В зависимости от решаемых задач различают изыскательские, ис­полнительные, инвентаризационные планы.

Под точностью понимают суммарную среднюю квадратическую погрешность в плановом и высотном положении точек ситуации и релье­фа, она вычисляется по формуле

Погрешности координат точек включают в себя ошибки развития планового обоснования, ошибки съемочных измерений и графических по­строений, погрешности вследствие деформации планшетов.

СНБ: средняя погрешность планового положения точек относительно пунктов опорной геодезической сети не должна превышать:-0,1 мм в масштабе создаваемого плана на открытой местности и застроенной территории;-0,15 мм в масштабе создаваемого плана для местности закрытой древесной и кустарниковой растительностью.

Средние погрешности высот точек съемочных геодезических сетей относительно ближайших реперов нивелирования II-IV класса не должны превышать 1/10 высоты сечения рельефа на равнинной местности и 1/6 высоты сечения рельефа на всхолмленной местности

Детальность - степень генерализации изображения, т. е. степень соотв. контуров и элементов рельефа на плане и на местности.(Чем меньше знаменатель масштаба плана, тем выше детальность плана.)

Выпрямление контуров и выступов зданий допускается, если по­грешность за обобщение четких контуров не превышает на плане 0,5 мм, а для архитектурных элементов - 0,3 мм.

Полнота плана - это степень его насыщенности элементами ситуа­ции и рельефа, изображение которых необходимо для проектирования и возможно при принятом масштабе плана и высоте сечения рельефа.Полнота плана выражается наименьшими размерами предметов и наименьшими расстояниями между предметами.

1/M=lплана/lмест

2. Уравнительные вычисления. Общие положения.

Уравнительные вычисления, общие положения.

Задача уравнивания возникает только при наличии избыточных измерений и ошибок измерений (ошибки измерений есть всегда).

В геодезической практике число выполненных измерений n всегда больше числа тех измерений к, которые следовало бы сделать, чтобы получить искомые величины (необходимые неизвестные). Измерения, которых было бы достаточно для определения этих неизвестных, назовем необходимыми. Разность г = n — к называется числом избы-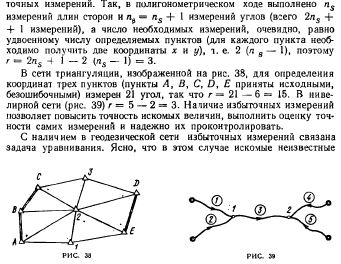

определяются неоднозначно и зависят от того, по каким измерениям они вычисляются. Задача уравнивания и заключается в том, чтобы, используя все измерения, получить однозначно все неизвестные.

Получение наиболее надежных значений этих величин и их оценка точности составляют задачу так называемых уравнительных вычислений (уравнивания). Уравнивание выполняют по методу наименьших квадратов (м. н. к.), согласно которому смеренные величины получают поправки V_I, удовлетворяющие условию [pv²]=min, где p_I — вес измерений.

Существуют два основных способа уравнивания: параметрический и коррелатный (ранее они назывались со ответственно способами посредственных и условных уравнений). В первом способе из решения так называемых нормальных уравнений получают непосредственно уравненные значения искомых величин — параметров, а во втором — сначала вспомогательные множители — так называемые коррелаты, а затем искомые величины n их функции. Оба способа уравнивания приводят к одинаковым результатам, но часто обладают различной трудоемкостью при решении одной и той же задачи. Так, например, при уравнивании полигонометрического хода, имеющего 10 определенных пунктов, параметрическим способом придется совместно решать 20 уравнений, а при коррелатном способе, как мы видели выше, всего 3. Следует, однако, иметь в виду, что число совместно решаемых уравнений, если задача решается на ЭВМ, не является определяющим критерием выбора того или иного способа уравнивания. Нужно учитывать также простоту составления исходных уравнений.

Кроме указанных двух способов уравнивания, существуют и так

называемые комбинированные способы, сочетающие достоинства одного и другого.