
- •Предисловие
- •Математическая символика
- •Введение
- •Глава 1. Линейные уравнения
- •§ 1.1. Уравнения с одной неизвестной
- •§ 1.2. Уравнения с двумя неизвестными
- •§ 1.3. Системы двух уравнений
- •§ 1.4. Системы трех и более уравнений
- •§ 1.5. Неравенства
- •Глава 2. Уравнения второго порядка
- •§ 2.1. Основные алгебраические тождества
- •§ 2.2. Квадратный трехчлен
- •§ 2.3. Уравнения с двумя неизвестными
- •§ 2.4. Симметричные формы
- •§ 2.5. Однородные многочлены
- •§ 2.6. Уравнения с тремя неизвестными
- •Глава 3. Уравнения старшего порядка
- •§ 3.1. Операции над многочленами
- •§ 3.2. Разложение многочленов на множители
- •§ 3.3. Неравенства
- •§ 3.4. Комплексные корни многочлена
- •§ 3.5. Формула Кардано
- •§ 3.6. Формула Феррари
- •§ 3.7. Границы корней многочлена
- •§ 3.9. Многочлены в других задачах
- •Задачи
- •Ответы
- •Древнегреческий алфавит
- •Биографические справки
- •Список литературы

§ 3.6. Формула Феррари |
161 |
познакомимся в одном из следующих выпусков нашей се- |
|
рии. Аналитическое представление корней кубического мно- |
|
гочлена может иметь очень даже громоздкий вид. При этом, |
|
чтобы примерно установить место корня на вещественной |
|
оси, нам все равно потребуется поработать. Поэтому ана- |
|
литическое решение интересно прежде всего в тех случаях, |
|
когда мы в дальнейшем собираемся исследовать полученное |
|
решение. Задачи, которые приведены в конце книги, пред- |
|
назначены для закрепления теории, и их решение не пред- |
|
полагает чрезмерно громоздких выкладок. |
|
Задачи к параграфу на с. 203, п. 36–38. |
|
§ 3.6. Формула Феррари
149 164 Первый шаг алгоритма нахождения корней многочлена четвертой степени
4 + 3 + 2 + +
также связан с заменой переменной. Сделаем подстановку
= − 4 , раскроем скобки и приведем подобные. Теперь задача сводится к нахождению корней неполного многочлена вида
4 + 2 + + .

162 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Введем вспомогательную переменную и преобразуем выражение многочлена к виду
|
|
|
2 |
|
2 |
|
( 2 + |
|
+ ) |
|
− [2 2 − + ( 2 + − + |
|
) ]. (6) |
2 |
|
4 |
||||
Полученное выражение тождественно исходному при любом значении . Теперь подберем такое значение , при котором выражение в квадратных скобках будет полным квадратом. Для этого достаточно найти значение , обращающее в ноль дискриминант квадратного трехчлена
|
|
2 |
|
|
|
|
|
|||
2 2 − + ( 2 + − + |
|
|
). |
|
|
|
|
|
||
|
4 |
|
|
|
|
|
||||
= 2 − 8 ( 2 |
|
|
|
|
|
|
2 |
|
|
|
+ − + |
|
) = |
|
|
||||||
4 |
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
||
= −8 3 − 8 2 − 8 ( |
|
− ) + 2. |
|
|
||||||
4 |
|
|
||||||||
= 0 3 + 2 + ( |
2 |
− ) − |
2 |
|
||||||
|
|
= 0. |
||||||||
4 |
8 |
|||||||||
Кубическое уравнение всегда имеет по крайней мере один вещественный корень. После того как выражение в квадратных скобках из формулы (6) будет представлено в виде полного квадрата, мы применим тождество для разности квадратов. Таким образом, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов, а задача нахождения корней многочлена сводится

§ 3.6. Формула Феррари |
163 |
|
|
к задаче нахождения корней двух квадратных трехчленов. |
|
||
Пример. Найти корни многочлена |
|
|
|
|
|
204 |
|
4 4 + 80 3 + 540 2 + 1496 + 1465.
Решение. Разделим левую и правую части уравнения на 4.
4 + 20 3 + 135 2 + 374 + 14654 = 0.
Сделаем подстановку = −5. Тогда уравнение примет вид
4 − 15 2 + 24 − 154 = 0.
Перепишем выражение в виде
( 2 − |
2 + ) |
2 |
− (2 2 − 24 + 2 − 15 + 60). |
|
|
15 |
|
|
|
= 276 − 8 ( 2 |
− 15 + 60) = −8 2 + 120 − 480 + 12. |
|||
|
|
|
|
= 0 3 − 15 2 + 60 − 72 = 0. |
Один вещественный корень = 3 мы можем «угадать» (теорема на с. 111). При = 0 квадратный трехчлен
2 2−24 + 2−15 +60 = 6 2−24 +24 = 6( 2−4 +4) = 6( −2)2.

164 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Следовательно,
|
|
|
|
|
|
|
|
|
|
|
|
( 2 − |
9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
( |
√6 · ( − 2) = |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
= ( 2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
√6 − 2 + 2√6)( 2 + √6 − 2 − 2√6). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|||
|
1) Найдем корни трехчлена |
2 |
− |
√ |
|
|
|
|
|
|
|
9 |
|
+ 2 |
√ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 − |
2 |
|
6. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
√2 + |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
√6 − |
29 |
− 2√6. |
|||||||||||||||||||||||||||||||||||||||||||
|
2) Найдем корни трехчлена |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= 4(6 − |
2 |
6); |
1,2 |
= |
2 |
|
± 2 |
|
6 |
− 2 |
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
6;√2 = |
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Ответ: |
|
|
|
|
|
|
|
− 2 |
= |
|
|
|
6 |
|
|
|
|
|
|
|
6 − 2 6; |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
1 = |
2 |
|
|
|
|
|
|
2 |
|
|
+ 2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
6 − 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
= 4(6 + 2 |
6); |
1,2 |
− |
2 |
|
|
± |
2 |
|
|
|
6 + 2 |
|
|
|
6. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
√ |
6 |
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
6 |
|
|
|
|
|
|
|
|
|
|
√ |
|
|
||||||
|
3 |
|
− 2 |
|
− 2 |
|
|
+ 2√6; |
|
|
|
|
|
3 |
= − |
2 + |
|
|
6 +√ . |
|||||||||||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
√ |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
√ |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
√ |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 6 |
|
|
|
|
||||||||||||||||||||
|
Формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Феррари так же, как и формула Кардано, не на- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
шла широкого применения на практике по причине своей |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
громоздскости. Если бы в примере мы взяли многочлен со |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
случайными коэффициентами, вероятно, для записи ответа |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
не хватило бы места на странице. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
Задачи к параграфу на с. 204, п. 39. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
§ 3.7. Границы корней многочлена
161 168 В этом параграфе нас будут интересовать только вещественные корни многочлена. Мы уже знаем, что поиск корней многочленов степени выше второй – дело непростое. Даже если мы применяем численные методы, для начала

§ 3.7. Границы корней многочлена |
165 |
неплохо бы знать, на каком интервале следует вести поиск.
Ведь ось бесконечная! Пусть дан многочлен
( ) = 0 + 1 −1 + · · · + −1 + .
→±∞ |
1 |
|
|
|
|
+ |
|
+ 0 |
|
|
||
−1 + 2 −2 |
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· · · |
|
|
|
||
lim |
|
|
|
|
|
|
|
0 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
2 |
+ |
· · · |
+ |
0 |
||||
|
|
|
→±∞ |
|
−1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
= +∞.
Таким образом, старший член по модулю растет быстрей всех остальных и, начиная с некоторой точки, превосходит модуль их суммы. Значения | |, выходящие за эту границу, не могут быть корнями. Теперь рассмотрим модуль многочлена 1 −1 + 2 −2 + · · · + 0. Очевидно,
| 1 −1 + 2 −2 +· · ·+ 0|≤ | 1|| | −1+| 2|| | −2+ · · ·+| |≤ ≤ ( | −1+| | −2+ · · · + 1), где = {| 1|, | 2|, · · · | |}.
По формуле суммы геометрической прогрессии,
( | −1+| | −2+ · · · + 1) = | | −1 < | | . | |−1 | |−1
Считаем | |> 1. Тогда условие
| 1 −1 + 2 −2 + · · · + 0|≤ | 0 |

166 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
выполняется, если |
|
|
|
|
|
|
|
|
|
|
||
|
| | |
|
|
|
|
|
|
|
|≥ |
|
|
+ 1. |
|
|
| |−1 |
| 0| |
|||||||||
|
| |−1 ≤ | 0|| | |
|
≤ | |
0| | |
|
|||||||
Заметим, что условие | |> 1 здесь действительно выполняется. Последнее неравенство задает два интервала, на которых не может быть корней многочлена. В таком случае
|
|
|
|
|
|
|
|
|
|
|
корни следует искать только на интервале | |< |
|
+1. Ина- |
||||||||
| 0| |
||||||||||
|
|
|
|
|
|
|||||
че говоря, − |
|
|
+ 1 ; + |
|
|
|
+ 1 . Мы только что |
|||
|
0 |
|
0 |
|||||||
определили верхнюю( (| |
границу| ) |
для(| корней| ) )многочлена. Сде- |
||||||||
лаем замену переменной = 1 |
. Тогда |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 + 1 −1 +· · ·+ −1 + = |
1 |
|
( + −1 −1 +· · ·+ 0). |
|||||||
|
||||||||||
|
||||||||||
При этом будем считать, что ̸= 0, т. е. = 0 не являет-
ся корнем исходного многочлена. Каждому корню нового
многочлена будет соответствовать корень = 1 исходного многочлена и наоборот. Теперь займемся границами корней многочлена в скобках. Пусть = {| 0|, | 1|, · · · | −1|}.
Тогда, как доказано выше, | |< |
|
+ 1. Отсюда |
|||||||
| | |
|||||||||
|
< |
+ 1 | |> + |
. |
||||||
|
1 |
|
|
|
|
|
|
| |
|
|
| | |
|
|
| |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

§ 3.7. Границы корней многочлена |
167 |
Следовательно, для корней многочлена всегда справедливо неравенство
|
|
|
|
| | |
< |
|
|
< |
|
+ 1 |
|
|
|
|
|
|
|||
|
|
|
|
+ | | |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
| | |
|
| 0| |
|
|
|
|
|
|
|
|||||
или, что то же самое, |
) |
( + |
|
|
|
|
|
+ 1), |
|||||||||||
(− |
0 |
− 1; − + |
; |
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
| | |
|
| |
|
| |
| | |
|
|
||||||||||
где = {| 1|, | 2|, · · · | |}, = {| 0|, | 1|, · · · | −1|}. |
|||||||||||||||||||
Пример 1. Определить границы вещественных |
|
204 |
|||||||||||||||||
корней многочлена 3 − 3 2 − 3 − 4.
Решение. С этим многочленом мы уже встречались на с. 154.
= {1, 3, 3} = 3, = {3, 3, 4} = 4 | | |
( |
7; 5). |
|||
|
|
|
4 |
|
|
Ответ: | | |
74 ; 5 . |
|
|
|
|
( |
) |
|
|
|
|
Пример 2. Определить границы вещественных |
|
|
|
204 |
|
корней многочлена 3 6 − 2 4 + 3 − 3 2 + 2. |
|
|
|
|
|
Решение: |
|
|
|
|
|
= {3, 2, 1, 3} = 3, = {2, 1, 3, 2} = 3 | | (0,4; 2). |
|||||
Ответ: | | (0,4; 2). |
|
|
|
|
|
Задачи к параграфу на с. 204, п. 40. |
|
|
|
|
|

168 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
§ 3.8. Интерполяционный многочлен
Лагранжа
164 173 Всем известно, что через две точки на плоскости
можно провести одну единственную прямую. Многие знают,
что через три точки, не лежащие на одной прямой, проходит
единственная парабола с уравнением = 2 + + . Воз-
никает вопрос: как построить многочлен, график которого
проходит через заданные точек плоскости? Рассмотрим
задачу для случая четырех точек: ( 1; 1), ( 2; 2), ( 3; 3) и
( 4; 4). Поскольку мы строим функцию, естественно потре-
бовать различные значения для = 1, 2, 3, 4; значения
могут совпадать. Теперь построим четыре вспомогательных
функции:
1( ) = |
( − 2)( − 3)( − 4) |
; |
|
|
|
( 1 − 2)( 1 − 3)( 1 − 4) |
|
||
|
2( ) = |
( − 1)( − 3)( − 4) |
; |
|
|
( 2 − 1)( 2 − 3)( 2 − 4) |
|||
|
|
|
||
|
3( ) = |
( − 1)( − 2)( − 4) |
; |
|
|
( 3 − 1)( 3 − 2)( 3 − 4) |
|||
|
|
|
||
4( ) = |
( − 1)( − 2)( − 3) |
. |
|
( 4 − 1)( 4 − 2)( 4 − 3) |
|
Нетрудно понять принцип их построения. Поскольку все
имеют различные значения, знаменатели дробей отличны от нуля. Каждая из четырех функций является много-

§ 3.8. Интерполяционный многочлен Лагранжа |
169 |
членом третьей степени от . А теперь попробуем в качестве аргумента ( ) подставить одно из значений , где
, = 1, 2, 3, 4.
{
1, если = ;
( ) =
0, если ̸= .
Осталось записать выражение:
( ) = 1 1( ) + 2 2( ) + 3 3( ) + 4 4( ).
Это и есть интерполяционный многочлен Лагранжа. Сумма многочленов третьей степени является многочленом степени не выше третьей, но может быть ниже третьей, если коэффициенты при старших членах сократятся. Из свойств вспомогательных функций следует: ( ) = . Таким образом, график построенного многочлена проходит через четыре заданные точки. Аналогичные рассуждения нетрудно воспроизвести и при построении многочлена по пяти и более точкам. Своим названием многочлен обязан выдающемуся французскому ученому Жозефу Луи Лагранжу, а под интерполяцией в математике подразумевают метод нахождения промежуточных значений функции по имеющемуся набору известных.
Пример 1. Построить многочлен Лагранжа, график кото- 204
рого проходит через точки (0; 2), (3; 3), (4; 4), (7; 10) и (8; 12).

170 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
Решение. По известным значениям абцисс {0, 3, 4, 7, 10} по-
строим вспомогательные функции:
1( ) = ( − 3)( − 4)( − 7)( − 8); 672
2( ) = ( − 4)( − 7)( − 8); −60
3( ) = ( − 3)( − 7)( − 8); 48
4( ) = ( − 3)( − 4)( − 8); −84
5( ) = ( − 3)( − 4)( − 7). 160
Поставив в качестве коэффициентов при вспомогательных функциях ординаты соответствующих точек, получим интерполяционный многочлен Лагранжа:
( ) = 2 1( ) + 3 2( ) + 4 3( ) + 10 4( ) + 12 5( ).
На графике (рис. 31) видно, что кривая действительно проходит через точки (0; 2), (3; 3), (4; 4), (7; 10) и (8; 12). Обычно не требуется приведения подобных в выражении многочлена Лагранжа, но если раскрыть скобки и привести подобные, многочлен будет выглядеть так:
( ) = −168013 4 + 101840 3 − 1680653 2 + 263420 + 2.
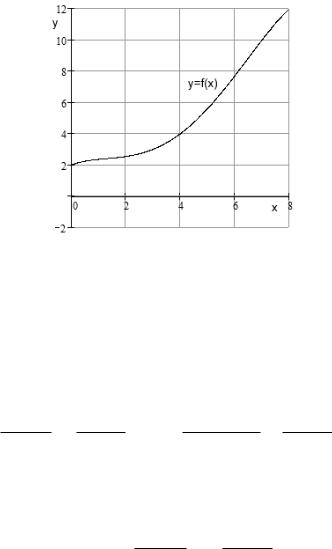
§ 3.8. Интерполяционный многочлен Лагранжа |
171 |
Рис. 31. График многочлена Лагранжа
Сомневающиеся могут убедиться в том, что
(0) = 2, (3) = 3, (4) = 4, (7) = 10 и (8) = 12.
В курсе математики средней школы выводят уравнение прямой, проходящей через заданные точки ( 1; 1) и ( 2; 2):
− 1 |
= |
− 1 |
|
= |
1 2 − 2 1 |
+ |
2 − 2 |
. |
2 − 1 |
2 − 1 |
|
|
|||||
|
|
2 − 1 |
2 − 1 |
|||||
Это же уравнение можно получить, сгруппировав по члены интерполяционного многочлена Лагранжа:
( ) = 1 |
− 2 |
+ 2 |
− 1 |
. |
1 − 2 |
|
|||
|
|
2 − 1 |
||
Теперь зададимся вопросом: какой вид будет иметь интерполяционный многочлен Лагранжа, если заданы три лежащие

172 ГЛАВА 3. УРАВНЕНИЯ СТАРШЕГО ПОРЯДКА
на одной прямой точки? Из теории (с. 80) следует, что пря-
мая не может пересечь параболу более чем в двух точках.
204 Пример 2. Построить многочлен Лагранжа, график кото-
рого проходит через точки (1; 2), (3; 6) и (9; 18).
Решение. Построим три вспомогательных многочлена:
1( ) = |
( − 3)( − 9) |
= |
|
( − 3)( − 9) |
; |
|
|
|
|
|
||||||
|
|
(1 − 3)(1 − 9) |
16 |
|
|
|
|
|
|
|
|
|||||
|
|
2( ) = |
( − 1)( − 9) |
= |
( − 1)( − 9) |
; |
|
|
||||||||
|
|
|
(3 − 1)(3 − 9) |
|
−12 |
|
|
|
|
|||||||
|
|
|
3( ) = |
|
( − 1)( − 3) |
= |
( − 1)( − 3) |
. |
|
|||||||
|
|
|
(9 − 1)(9 − 3) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
48 |
|
|
|||||
Тогда многочлен Лагранжа примет вид |
|
|
|
|
|
|
||||||||||
( ) = 2 |
( − 3)( − 9) |
+ 6 |
( − 1)( − 9) |
|
+ 18 |
( − 1)( − 3) |
. |
|||||||||
|
|
16 |
|
|
|
|
−12 |
|
|
|
|
48 |
|
|
||
Раскрыв скобки в правой части равенства, придем к урав-
нению = 2 . Алгоритм «распознал», что ему вместо пара-
болы «подсунули» прямую.
Ответ: = 2 .
Рассмотрим еще одну задачу. Требуется найти квадратный
трехчлен, если известны его корни 1 и 2, а его график
проходит через точку ( 0; 0). В таком случае коэффици-
енты при вспомогательных многочленах, соответствующих
1 и 2, нулевые, поэтому достаточно построить один вспо-
могательный многочлен, соответствующий 0, и многочлен
