Стоит ли поднимать цены?

Конкуренция, цена и доход

Когда вы захотите купить бутылку воды в поезде, или мороженое в кино вас может отпугнуть цена. Как они что-то продают при таких ценах? Дело в том, что эти фирмы не принимают существующие цены на рынке. Они могут выбирать, какую цену назначить. Эластичность спроса по цене может объяснить их поведение. Возьмем пример с бутылкой воды в поезде. Если вы хотите пить и у вас нет с собой напитков, вам придется купить бутылку воды в вагоне-ресторане или мириться с жаждой. Другого выхода нет. А значит, спрос на бутылку воды в поезде неэластичен при нормальной магазинной цене. Это значит, что цены на напитки и еду в поезде могут быть подняты для зарабатывания дополнительного дохода.

В общем, чем меньше конкурентов y фирмы, тем ниже эластичность спроса на ее продукцию , так как на рынке мало товаров-заменителей, на потребление которых могут перейти покупатели. Чем ниже эластичность спроса по цене, тем выше будет назначаемая фирмой цена.

Когда на рынке много конкурирующих фирм, дело обстоит иначе. Бензоколонки, расположенные неподалеку друг от друга, могут вести жесткую конкурентную борьбу при помощи цен. Владельцы одной бензоколонки могут надеяться, что, снизив цену за литр бензина на 1 пенс или даже на 0,1 пенса, они привлекут больше клиентов, пользующихся услугами другой бензоколонки. При очень эластичном спросе небольшое снижение цены может привести к значительному повышению дохода. Проблема только в том, что когда все бензоколонки снизят цену, никто из них не выиграет. Никто не привлечет к себе чужих клиентов. B этом случае выигрывает клиент.

Измерение эластичности

Мы определили эластичность по цене как отношение процентного или пропорциольного изменения количества товара, пользующегося спросом, к процентному или пропорциональному изменению цены. Но как на практике можно измерить это изменение для определенной кривой спроса?

Студенты часто делают ошибку, считая, что могут говорить об эластичности всей кривой. Ошибка заключается в том, что эластичность на разных отрезках кривой в большинстве случаев различна.

Возьмем, к примеру, кривую спроса на рис. a. Между точками a и b общий объем затрат потребителей растет (Р2Q2 > P₁Q1): спрос эластичен между этими точками. Между точками c и b общий доход уменьшается (Р3Q₃ < Р2Q2). Здесь спрос неэластичен. Поэтому мы обычно говорим об эластичности части кривой спроса, a не всей кривой. Однако есть два исключения из правила. Первое - когда эластичность оказывается одинаковой на всем протяжении кривой, как в особых случаях, показанных на рис. 2.5. Второе – когда две кривые изображены на одном графике, но имеют разный угол наклона. При любой цене они будут иметь разную эластичность.

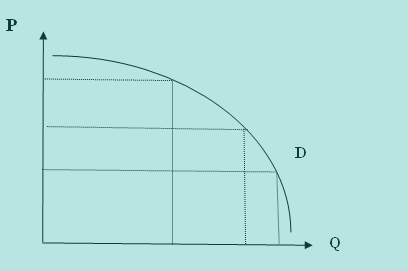
Рис. a. Различная эластичность на разных отрезках кривой спроса (по вертикали – цена, по горизонтали – объем)

Хотя обычно нельзя говорить об эластичности всей кривой, можно сделать вывод об эластичности между любыми двумя точками на ней. Рис. а показывает разное значение эластичности спроса по цене для двух разных точек.

Для определения эластичности спроса по цене мы используем формулу:

Мы измеряем пропорциональное изменение количества товара, деля это изменение на уровень Q, т. e. ^Q/Q. Таким же образом измеряется пропорциональное изменение цены: ^P/Р. Эластичность спроса по цене может быть записана следующим образом:

Но какое значение передают P и Q? Посмотрим на данные по спросу, приведенные в таблице. Какова эластичность спроса, определяемая ценами 8 и 6 фунтов? Чтобы ответить на этот вопрос, надо определить ^Q и Q, ^Р и P. Начнем с количества товара.

Таблица

Цена, фунты	8	6	4	2
Количество товара, тыс. ед.	10	20	30	40

Изменение количества (^Q) между 10 и 20 равно 10 ед.

^Q = 10. Но каково пропорциональное изменение Q (^Q/Q)? Равно ли оно 10/10, если взять Q = 10 как точку, от которой измеряется изменение Q? Или 10/20, если взять Q = 20 как точку, от которой измеряется изменение Q? Чтобы избежать этой проблемы, используют среднее арифметическое этих количеств, т. e. середину между двумя точками:

следовательно,

Цена

Разница в цене между 8 и 6 равна 2, т.е. ^P =-2.

Пропорциональное изменение P вычисляется так же, как и пропорциональное изменение Q. В качестве базовой цены берется среднее арифметическое цен, т. e. середина между двумя точками: P = 7, т. e. (8 + 6)/ 2,

следовательно,