" Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча. Для булевой функции двух переменных диаграмма Вейча имеет вид (табл. 4.4.1).

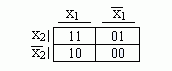
Каждая клетка диаграммы соответствует набору переменных булевой функции в ее таблице истинности. В (табл. 4.4.1) это соответствие показано, В клетке диаграммы Вейча ставится единица, если булева функция принимает единичное значение на соответствующем наборе. Нулевые значения булевой функции в диаграмме Вейча не ставятся. Для булевой функции трех переменных диаграмма Вейча имеет следующий вид (табл. 4.4.2).

Добавление к ней еще такой же таблицы дает диаграмму для функции 4-х переменных (табл. 4.4.3).

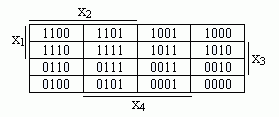
Таким же образом, т. е. приписыванием еще одной диаграммы 3-х переменных к только что рассмотренной, можно получить диаграмму для функции 5-ти переменных и т. д., однако диаграммы для функций с числом переменных больше 4-х используются редко. Для приведенных диаграмм характерно следующее:

• каждой клетке диаграммы соответствует свой набор;

• соседние наборы расположены рядом в строке либо в столбце.

Соседними наборами называются наборы, отличающиеся одной компонентой. Напомним, что конституенты, соответствующие таким наборам, склеиваются (см. метод Квайна- Мак-Класки). Например, для функции, заданной табл. 9.22,

конституенты, соответствующие паре единиц в левой части таблицы, склеиваются и порождают элементарное произведение из 2-х букв:

х₁х₂/х₃ v x₁x₂x ₃ = x₁x₂

О паре единиц в правой части диаграммы можно сказать то же самое:

/х₁х₂/х₃ v /x₁/x₂/x ₃ = /x₁/x₃

Отметим, что получающееся элементарное произведение легко определить сразу по диаграмме: это произведение переменных, принимающих одно и то же значение в обеих клетках. Еще одно важное замечание: столбцы, расположенные по краям диаграммы, тоже считаются соседними. Для нашего примера это означает, что имеет место еще одно склеивание, в результате которого, следуя указанному правилу, получаем элементарное произведение x₂/x₃ Из рассмотренных ранее методов нам известно, что возможно дальнейшее склеивание получаемых элементарных произведений. На диаграммах Вейча они тоже располагаются рядом. Общее правило склеивания на диаграммах Вейча можно сформулировать следующим образом: склеиванию подлежат прямоугольные конфигурации, заполненные единицами и содержащие число клеток, являющееся степенью 2. Получающееся новое элементарное произведение определяется как произведение переменных, не меняющих своего значения на всех склеиваемых наборах. Число m оставшихся переменных в элементарном произведении определяется легко:

m = n - log₂M

где n - число переменных функции, М - число склеиваемых наборов. Метод широко используется на практике, благодаря простоте и удобству. После небольшой тренировки достигается элементарный навык определения минимальной ДНФ по диаграмме "с первого взгляда". Минимизация булевой функции заключается в нахождении минимального накрытия всех единиц диаграммы Вейча блоками из единиц (указанной конфигурации), расположенных в соседних клетках диаграммы. При этом всегда считается, что левый край диаграммы Bейча 4-х переменных примыкает к ее правому краю, а верхний oкрай диаграммы примыкает к нижнему ее краю. После получения минимального накрытия всех единиц диаграммы Вейча, минимальная ДНФ булевой функции записывается как дизъюнкция элементарных конъюнкций, соответствующих выделенным блокам единиц в диаграмме. Рассмотрим несколько примеров. Пример. Булева функция f имеет следующую СДНФ:

f=х₁х₂х₃ v х₁/х₂х₃ v /х₁/х₂/х₃ v /х₁/х₂/х₃ v х₁х₂/х₃.

Найти минимальную ДНФ с помощью диаграммы Вейча. Диаграмма Вейча, соответствующая функции f, представлена в табл. 4.4.5. Минимальное накрытие всех единиц диаграммы возможно только блоками по две единицы. Каждому такому блоку соответствует своя конъюнкция, как показано в табл. 4.4.5.

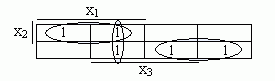
Следовательно, минимальная ДНФ функции имеет вид:

f = х₁х₂ v /х₁/х₂ v х₁х₃.

Пример.

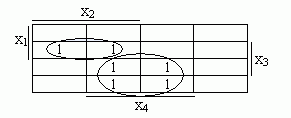
f₁=х₁х₂х₃ v /х₁х₄.

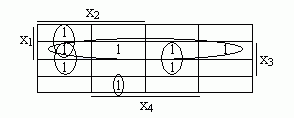
f₂=х₁х₂х₄ v х₂х₃/х₄ v х₁х₃ v /х₂х₃х₄ v х₁х₂х₃x₄.

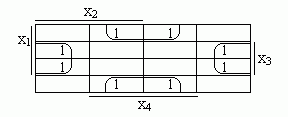
f₃=х₃/х₄ v /х₃х₄.

f₄=/х₃х₄ v /х₁х₄ v х₁х₃/х₄.

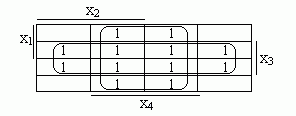
f₅=х₃ v х₄.

f₆=х₃х₄ v /х₃/х₄ v х₁х₂х₃. "

Это эквивалентные понятия, обозначающие один и тот же способ минимизации булевых функций. Этот способ является графическим. Его предложил в 1952 Эдвард В. Вейч, а доработал и усовершенствовал, немного позже в 1953, Морис Карно.

Итак, карты Карно для функций 1-ой, 2-х, 3-х переменных выглядят вот так:

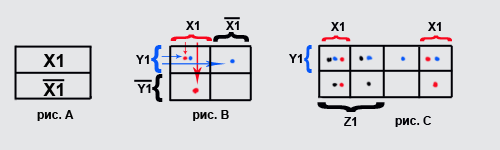
Исходным материалом для работы с данным графическим методом минимизации возьмем известную нам таблицу истинности, хотя в принципе карты Карно (диаграммы Вейча) можно назвать упрощенной таблицей истинности, ну ничего страшного если немного попрактикуемся. В качестве примера используем функцию 4-х переменных.

Таблица истинности будет выглядеть вот так:

Исходя из данной таблицы, получим СДНФ, которая будет выглядеть таким образом:

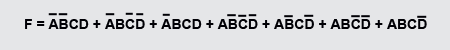
Следующим шагом минимизации функции будет заполнение соответствующих клеток  карты Карно (диаграммы Вейча). Для функции 4-х переменных она имеет вид поля с ячейками четыре на четыре.

На основании СДНФ заполним соответствующие ячейки. Получится вот такой вид карты Карно:

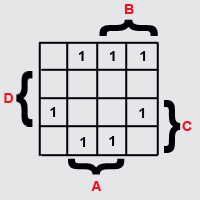
Далее очень важным моментом для понимания является осознание того, что данная карта не является квадратом или прямоугольником, а является цилиндром, сгибающимся как по горизонтали, так и по вертикали, а ячейки находящиеся по краям, тоже имеют соседей как слева, так и справа.

Выглядит это примерно вот так: Верх и низ цилиндра тоже соседи.

Принимая во внимание свойства “цилиндра” произведем заключительный этап минимизации логической функции, т.е. произведем склеивание единиц. При выполнении этого процесса количество склеиваемых единиц должно быть кратно 2 и изменять значение “истина (1)” “ложь (0)”, может только одна переменная. На рисунке также обозначим комбинации склеивания единиц (каждая склейка имеет один цвет) и количество сомножителей им соответствующее. Отобразим это все на рисунке. 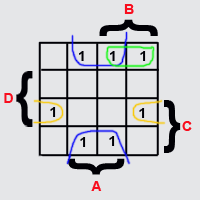Таким образом, конечное минимизированное значение функции примет следующий вид:

Однако при рассмотрении способа минимизации логической функции при помощи карт Карно, практически всегда можно встретить изображение вот такого вида. Для нашего случая это будет выглядеть так: Данная карта Карно – это точно такая, как и предложенная ранее с той лишь разницей, что по обеим сторонам представлен так называемый код Грея (т.е. соседние значения отличаются только одним разрядом). Склеивание “единиц” производится ранее описанным способом, т.е. по изменению одной переменной, и их количество должно быть кратно 2.

Таким вот графическим методом производится минимизация логических функций. Надеюсь, описал доступно и понятно.

Порядок проектирования комбинационных схем

При проектировании схем, выполняющих ту или иную логическую функцию, необходимо обеспечить минимизацию аппаратных затрат на реализацию этих схем, а также во многих случаях необходимо сократить номенклатуру используемых логических элементов. Последнее требование реализуется путем выбора соответствующей системы элементов. В настоящее время основные серии интегральных логических схем включают в себя элементы, составляющие некоторый функционально полный логический базис, а также дополнительные элементы, реализующие часто встречающиеся логические функции [ 1 ] . В качестве функционально полных базисов используются, как правило, одноэлементные базисы "И-НЕ" либо "ИЛИ-НЕ".

Рассмотрим этапы проектирования комбинационных логических схем на одноэлементном базисе "И-НЕ" без использования каких-либо дополнительных логических элементов на примере проектирования одноразрядного комбинационного сумматора. Такой сумматор является основой построения многоразрядной суммирующей схемы, выполняющей операции над числами, представленными в том или ином коде.

Пример выполнения операции суммирования чисел, представленных в обратном коде:

X^ок=0.1011

Y^ок=1.0110

₊0.1011

1.0110

₊1.0.0001

_______1

0.0010

Из примера видно, что в каждом разряде происходит суммирование соответствующих разрядов операндов и переноса, поступающего из предыдущего разряда (для младшего разряда – циклический перенос из знакового разряда). При этом вырабатывается значение суммы в этом разряде и перенос в следующий разряд.

Условно-графическое обозначение элемента, выполняющего эти действия, приведено на рис. 13.4.

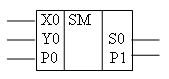
Рис. 13.4. Условно-графическое обозначение одноразрядого сумматора

Рассмотрим основные этапы проектирования такой схемы.

Этап 1. Представление функции, выполняемой проектируемой схемой, в каноническом виде, то есть в виде таблицы истинности или одной из совершенных нормальных форм записи. Обычно на этом этапе функцию легче описать таблицей истинности. Так как проектируется двухвыходная логическая схема, то необходимо представить таблицу истинности для каждого ее выхода (табл. 13.6).

Таблица 13.6.
Входы			Выходы
Xi	Yi	Pi	Si	Pi+1
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Этап 2. Минимизация логической функции. На этом этапе можно использовать любые методы минимизации [ 5 ] . Специфика минимизации многовыходных функций – необходимость получения устройства, имеющего минимальный общий состав оборудования, то есть следует проводить минимизацию одной функции с учетом возможного использования части полученного оборудования для минимизации другой функции. В нашем примере не будем рассматривать эту особенность и проведем автономную минимизацию каждой функции. Минимизацию логических функций можно проводить различными методами: методом Квайна, его модификацией – методом Квайна – Мак-Класки, методом диаграмм Вейча. Метод диаграмм Вейча удобно использовать для минимизации функций от небольшого (до четырех) числа переменных. Диаграмма Вейча для функции S_i представлена в табл. 13.7.

Таблица 13.7. Диаграмма Вейча для функции суммы одноразрядного сумматора
	yi		yi
xi	0	1	0	1
xi	1	0	1	0
	pi	pi		pi

Из диаграммы видно, что минимальная дизъюнктивная нормальная форма для функции суммы одноразрядного сумматора совпадает с ее совершенной дизъюнктивной нормальной формой:

Диаграмма Вейча для функции P_i+1 представлена в табл. 13.8.

Таблица 13.8. Диаграмма Вейча для функции переноса одноразрядного сумматора
	yi		yi
xi	1	1	1	0
xi	0	1	0	0
	pi	pi			pi

Минимальная дизъюнктивная нормальная форма для этой функции имеет вид:

Этап 3. Перевод функции в базис, в котором будет строиться схема. В выбранном варианте это базис "Штрих Шеффера":

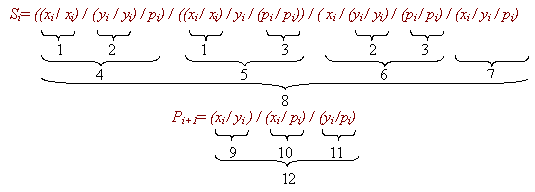
Этап 4. Составление схемы на элементах, реализующих функции выбранного базиса. Для более наглядного отображения этого этапа выше обозначены номера элементов, которые будут реализовывать ту или иную часть функции. Полученные схемы представлены на рис.13.5 и 13.6.

Рис. 13.5. Схема, реализующая функцию суммы одноразрядного сумматора

Рис. 13.6. Схема, реализующая функцию переноса одноразрядного сумматора

Значит так. Таблица истиннности такая: x1 x2 x3 y 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0 теперь рисуем собственно диаграмму: x2 x2 !x2 !x2 x1 1 0 1 0 !x1 0 0 1 1 !x3 x3 x3 !x3 То есть расставляем 1 туда, где они стоят в таблице истинности (! - не, то есть отрицание) Первая ячейка - x1 = 1, x2 = 1, x3 = 0. Подпись показывает, где какое значение переменной должно быть. Там, где ! - соответствующая переменная = 0, где его нет - 1. Теперь строим функцию. Все 1 должны быть закрыты соответствующим произведением, причем 2, 4 или 8 рядом стоящих 1 можно объединять и закрыть одним произведением или даже одной переменной. Таблица не плоская, она свернута по длинной стороне, то есть 1-я колонка соприкасается с 4-й, однако в данном случае нас это не интересует - таких соприкосновений нет. Каждая 1 должна быть закрыта. Пишем. Имеем 2 пары 1, стоящих рядом (строка 2 столбцы 3,4 и столбец 3) и 1 единица отдельно. Соответственно, имеем функцию: y = x1^x2^!x3 V !x2^x3 V !x1^!x2, поскольку: - отдельная единица зависит от всех переменных - пара в столбце 3 не зависит от значения x1 - пара в строке 2 не зависит от значения x3 Если бы было 4 единицы рядом (строка или квадрат), они дали бы член, состоящий только из 1 переменной, поскольку не зависиле бы от 2 других.

Системы логических элементов

Системой логических элементов называется функционально полный набор логических элементов, объединенных общими электрическими, конструктивными и технологическими параметрами и использующих одинаковый тип межэлементных связей [1]. Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реа-лизующие функции узлов ЭВМ, а также элементы для усиления, восстанов-ления и формирования сигналов стандартной формы.

Условно-графические обозначения (УГО) некоторых логических элементов представлены на рис.13.1.

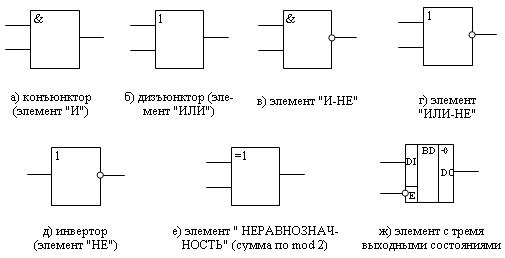Рис. 13.1.  Условно-графические обозначения логических элементов

УГО элемента представляет собой прямоугольник, к которому слева подходят входные сигналы, а справа выходят выходные. Внутри прямоугольника ставится условное обозначение выполняемой элементом логической функции. Если значение выходного сигнала принимает инверсное значение по отношению к обозначенной внутри элемента функции, то данный выход обозначается на УГО элемента кружком (рис.13.1,в – 13.1,д). Аналогично, если активным уровнем входного сигнала является логический "0", то данный вход обозначается кружком (вход E элемента 13.1,ж ).

Если элемент выполняет сложную функцию, имеет несколько функционально различных групп входов и выходов, то входы и выходы отделяются от основного поля УГО вертикальными линиями. Внутри каждого из получившихся полей функционально различные группы входов и выходов отделяются друг от друга горизонтальными линиями. На рис.13.1,ж показан элемент, выход которого может находиться в одном из трех состояний: логический "0", логическая "1", состояние высокого сопротивления. В состоянии высокого сопротивления выход элемента отключается от входов всех других элементов, с которыми он связан. Вход E (enable) этого элемента управляет состоянием его выхода. Так как на условно-графическом обозначении этот вход отмечен кружком, то отсюда следует, что функция разрешения передачи двоичного сигнала с входа на выход элемента выполняется при состоянии логического "0" на входе разрешения E. Если на вход E подан сигнал логической "1", то выход элемента находится в отключенном (так называемом "третьем") состоянии.

Каждый логический элемент – это электронно-техническое изделие (рис.13.2). В этих схемах все транзисторы работают в ключевом режиме. Это означает, что при подаче сигнала высокого уровня на базу транзистора, его сопротивление становится пренебрежимо малым, то есть транзистор как бы "стягивается в точку". При низком потенциале на базе транзистора сопротивление между коллектором и эмиттером становится чрезвычайно большим, что фактически означает разрыв цепи.

Рис. 13.2.  Схемотехническая реализация логических элементов

Рассмотрим это на примере работы инвертора (рис.13.2,а). Если сигнал X имеет высокий потенциал, то ключ, реализованный на транзисторе, замкнут, и потенциал точки Y низкий. В противном случае связь между точкой Y и "землей" разорвана, и сигнал Y имеет высокий уровень, что и обеспечивает реализацию логической функции "отрицание".

Для элемента "И-НЕ" сигнал в точке Y будет иметь низкий уровень (НУ) лишь тогда, когда оба сигнала X1 и X2 имеют высокий уровень (ВУ). Работа этого элемента описывается таблицей 13.1.

Таблица 13.1. Работа элемента "И-НЕ"
X1	X2	Y
НУ	НУ	ВУ
НУ	ВУ	ВУ
ВУ	НУ	ВУ
ВУ	ВУ	НУ

Таблица 13.2. Таблица истинности функции "И-НЕ"
X1	X2	Y
0	0	1
0	1	1
1	0	1
1	1	0

Эта таблица соответствует логической функции "И-НЕ".

В то же время, принимая высокий уровень сигнала за логический "0", а низкий уровень – за логическую "1", получим следующую таблицу истинности (табл. 13.3).

Таблица 13.3. Таблица истинности функции "ИЛИ-НЕ"
X1	X2	Y
1	1	0
1	0	0
0	1	0
0	0	1

Эта таблица соответствует уже функции "ИЛИ-НЕ".

Таким образом, кодирование сигналов в системе логических элементов может влиять на выполняемую им логическую функцию. В дальнейшем будем полагать кодировку сигналов, принятую для табл. 13.2.

Для элемента "ИЛИ-НЕ" (см. рис.13.2) сигнал в точке Y будет иметь высокий уровень лишь тогда, когда оба сигнала X1 и X2 имеют низкий уровень. Работа этого элемента описывается табл. 13.4, а его таблица истинности при сделанных предположениях о кодировке сигнала – таблицей 13.5. Эта таблица соответствует логической функции "ИЛИ-НЕ".

Таблица 13.4. Работа элемента "ИЛИ-НЕ"
X1	X2	Y
НУ	НУ	ВУ
НУ	ВУ	ВУ
ВУ	НУ	ВУ
ВУ	ВУ	НУ

Таблица 13.5. Таблица истинности функции "ИЛИ-НЕ"
X1	X2	Y
0	0	1
0	1	0
1	0	0
1	1	0

Параметры элементов принято делить на статические и динамические [1]. Статические параметры инвариантны к переходным процессам и измеряются в статическом режиме. Динамические, наоборот, определяют реактивные свойства элемента и измеряются во время переходных процессов.

К статическим параметрам относятся токи, текущие по выводам схемы, и соответствующие напряжения. Отметим среди этих параметров следующие:

• ток потребления;

• напряжение источника питания;

• пороговое напряжение низкого уровня (U⁰);

• пороговое напряжение высокого уровня (U¹);

• потребляемая мощность;

• нагрузочная способность;

• помехоустойчивость.

Среди многочисленных динамических параметров, характеризующих схему, выделим следующие:

• время перехода при включении (t¹⁰) (задний фронт);

• время перехода при выключении (t⁰¹) (передний фронт);

• время задержки распространения при включении (t⁰¹_зд);

• время задержки распространения при выключении (t¹⁰_зд);

• среднее время задержки распространения (t_{зд ср}) – интервал времени, равный полусумме времен задержки распространения сигнала при включении и при выключении; в дальнейшем это время будем называть временем задержки элемента (t_зд ).

Проиллюстрируем некоторые статические и динамические параметры логических схем на примере работы элемента "НЕ" (см. рис. 13.2,а). Временная диаграмма входного и выходного сигналов этого элемента, на которой отмечены его статические и динамические параметры, приведена на рис. 13.3.

Рис. 13.3.  Статические и динамические параметры элемента «НЕ»