Метод і експериментальна установка

Опис установки. Мікроскоп є одним з найважливіших лабораторних приладів у медичних і біологічних дослідженнях. Мікроскопи широко застосовують для спостереження і дослідження таких об'єктів, що неможливо розрізнити неозброєним оком.

У цій лабораторній роботі ми будемо використовувати біологічний мікроскоп для вимірювання біологічних об’єктів.

Побудова зображення предмета в мікроскопі подана на рис. 2.1. Оптична система мікроскопа складається з двох систем лінз: об'єктива й окуляра. Для простоти побудови зображення (рис. 2.1) система лінз об'єктива замінена однією збираючою лінзою Л_І, а система лінз окуляра – лінзою Л₂ Предмет АВ переміщується перед об'єктивом; трохи далі його фокуса. Об'єктив створює збільшене дійсне зображення А'В' предмета поблизу переднього фокуса окуляра, що розглядається оком через окуляр. Можливі три випадки взаємного розташування окуляра і зображення А'В': 1) зображення А'В' знаходиться трохи ближче переднього фокуса окуляра F₂ (окуляр створює збільшене уявне зображення А"В", що проектується на відстань найкращого зору); 2) зображення А'В' лежить у фокальній площині окуляра (зображення, утворюване окуляром, проектується на нескінченність і око спостерігача, працює без акомодації); 3) зображення А'В' знаходиться далі переднього фокуса окуляра (зображення, утворюване окуляром, буде дійсним, збільшеним). Таке розташування окуляра застосовується для мікропроекції і мікрофотографії. Збільшення мікроскопа Г дорівнює

,

де Δ – оптична довжина тубуса; S – відстань найкращого зору; f₁ – фокусна відстань об'єктива; f₂ – фокусна відстань окуляра.

Можна припустити, що підбираючи відповідним чином значення розмірів ƒ₁, ƒ₂ і Δ, одержимо мікроскоп із різним збільшенням. Проте на практиці використовують мікроскопи зі збільшенням понад 1500 – 2000 разів, тому що можливість розрізнення дрібних деталей об'єктивом мікроскопа обмежена. Це обмеження відбувається під впливом дифракції світла, що відбувається в структурі аналізованого об'єкта. У зв'язку з цим користуються поняттями межа розрізнення і розрізнююча спроможність мікроскопа.

Межа розрізнення мікроскопа визначається за формулою:

Ζ = λ/(2n sin u ),

де λ – довжина хвилі світла, що освітлює предмет; п – показник заломлення середовища між об'єктивом і предметом; u – апертурний кут об'єктива, рівний половині кута між крайніми променями конічного світлового пучка, що входить в об'єктив мікроскопа. Величина А = n sin u є числовою апертурою. Тоді

Ζ = λ/(2A) . (2.1)

Ця формула справедлива у випадку освітлення предмета збіжним пучком променів.

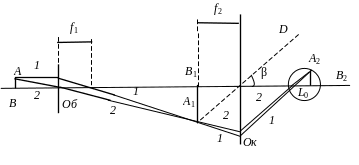
Рис. 2.1. Побудова зображення предмета у мікроскопі

З огляду на наявність межі розрізнення мікроскопа, межі розрізнення ока, вводять поняття корисного збільшення мікроскопа. Це таке збільшення, при якому мікроскоп створює зображення предмета, що має розміри, рівні межі розрізнення Z мікроскопа, і розміри цього зображення дорівнюють межі розрізнення Z_гл неозброєного ока на відстані найкращого зору

Г = Ζ_гл./ Ζ. (2.2)

Нормальне око на відстані найкращого зору розрізняє дві точки предмета, якщо кутова відстань між ними не менша 1', що відповідає

відстані між цими точками порядку 70 мкм. У цьому випадку корисне збільшення буде мінімальним:

Г_min = 70 / Ζ .

Вважають, що око найменше стомлюється при розгляданні предметів, розміри яких у 2 – 4 рази більше межі розрізнення ока (на відстані найкращого зору). Тому звичайно використовують мікроскопи з корисним збільшенням у межах 2Г_min - 4Г_min .

Якщо у формулу (2.2) підставити формулу (2.1), отримаємо

Г = 2 Ζ_гл A / λ.

При освітленні об'єкта білим світлом довжину хвилі вважають рівною 0,555 мкм, тому що око до нього найбільш чутливе. Таким чином, корисне збільшення мікроскопа звичайно знаходиться в інтервалі 500А<Г< 1000А.

У медичних і біологічних дослідженнях мікроскоп часто використовують для виміру розмірів малих об'єктів. З цією метою мікроскоп обладнують спеціальним пристроєм – окулярно-гвинтовим мікрометром, що являє собою насадку, що одягається на верхній кінець тубуса мікроскопа замість окуляра.

Оптична частина мікрометра складається з лінзи-окуляра, нерухомо закріпленої скляної шкали і рухливої скляної пластини, на якій нанесені перехрестя і два вертикальні штрихи над ним, паралельні рискам шкали.

Скляна пластина з перехрестям переміщується вздовж шкали мікрометра за допомогою мікрометричного гвинта.

Окулярно-гвинтовий мікрометр закріплюють на тубусі так, щоб скляна шкала знаходилася в площині, у якій розташоване дійсне зображення предмета, що утворює об'єктив мікроскопа. При цьому зображення шкали при розгляданні в окуляр сполучається з зображенням предмета. Переміщуючи за допомогою мікрогвинта рухливу пластину, можна сполучити перехрестя спочатку з одним краєм аналізованого предмета, а потім з іншим. При цьому можна визначити, якій кількості рисок шкали мікрометра відповідає дане зображення.

Переміщення пластини з перехрестям на одну поділку шкали мікрометра відповідає одному повному оберту мікрометричного гвинта. Барабан мікрометричного гвинта розділений на 100 рисок; отже, за допомогою окулярно-гвинтового мікрометра можна робити виміри предметів з точністю до 0,01 поділки шкали.

Для визначення розмірів предмета необхідно знати ціну поділки окулярно-гвинтового мікрометра. Під ціною поділки окулярно-гвинтового мікрометра розуміють виражену в міліметрах довжину відрізка, що аналізується у мікроскопі, зображення якого займає одну поділку шкали мікрометра.

Для визначення ціни поділки окулярно-гвинтового мікрометра застосовують об'єктний мікрометр – шкалу з відомою ціною поділки. Об'єктний мікрометр розглядають під мікроскопом як предмет і, поєднуючи в полі зору об'єктну і окулярну шкали, визначають ціну поділки окулярного мікрометра.

Для цієї мети можна також використовувати будь-який предмет, розмір якого відомий. Зокрема, для градуювання окулярно-гвинтового мікрометра застосовують розрахункову камеру Горяєва, використовувану в медичних вимірюваннях для підрахунку формених елементів крові. Камера Горяєва являє собою скляну пластинку, на якій нанесена сітка, що розбиває поле зору на квадрати з відомою довжиною сторони: сторона малого квадрата – 0,05 мм, великого – 0,2 мм.

На рис. 2.2 зображений зовнішній вигляд (а) і схема пристрою (б) біологічного мікроскопа. Оптична система мікроскопа ділиться на дві частини: освітлювальну і спостережливу. Освітлювальна частина складається з рухливого дзеркала 1, яке направляє промені від освітлювача на аналізований об'єкт, конденсора 2, що утворює на

об'єкті збіжний пучок світла; знімального світлофільтра 4 і укріпленої на конденсорі ірисової апертурної діафрагми 3 для регулювання освітленості об'єкта. Спостережлива частина складається з об'єктива 5, окуляра 7 і призми 6, що служить для направлення вертикальних променів, що пройшли об'єктив, в похилий тубус. Об'єктив являє собою систему лінз, зібраних в єдиній оправі. Передня лінза служить для збільшення, інші – призначені для виправлення недоліків зображення, отриманого передньою лінзою. Окуляр мікроскопа звичайно складається з двох лінз: верхньої – для ока і нижньої – збираючої, необхідної для того, щоб усі промені, що пройшли через об'єктив, потрапили в лінзу окуляра.

Біологічний мікроскоп має три об'єктиви, які дають різноманітне збільшення, що закріплені в револьвері 11, і три змінних окуляри.

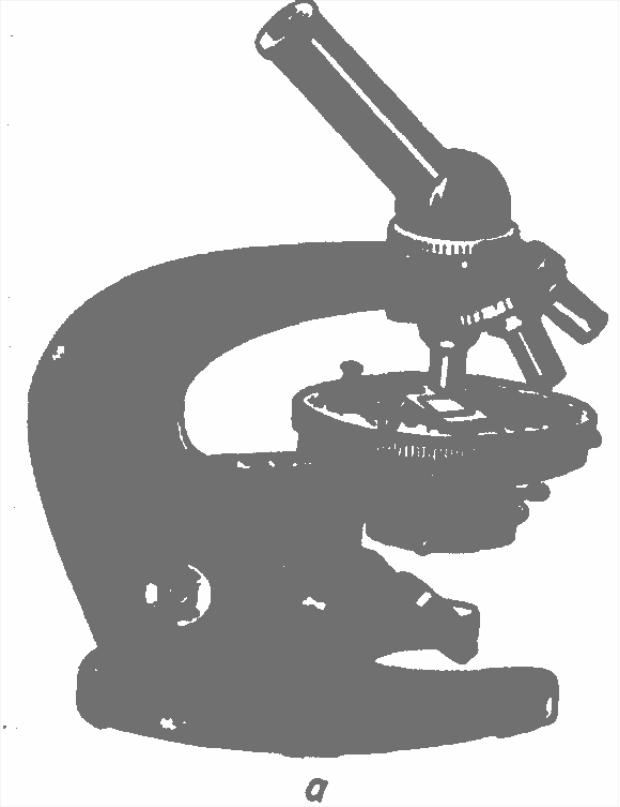
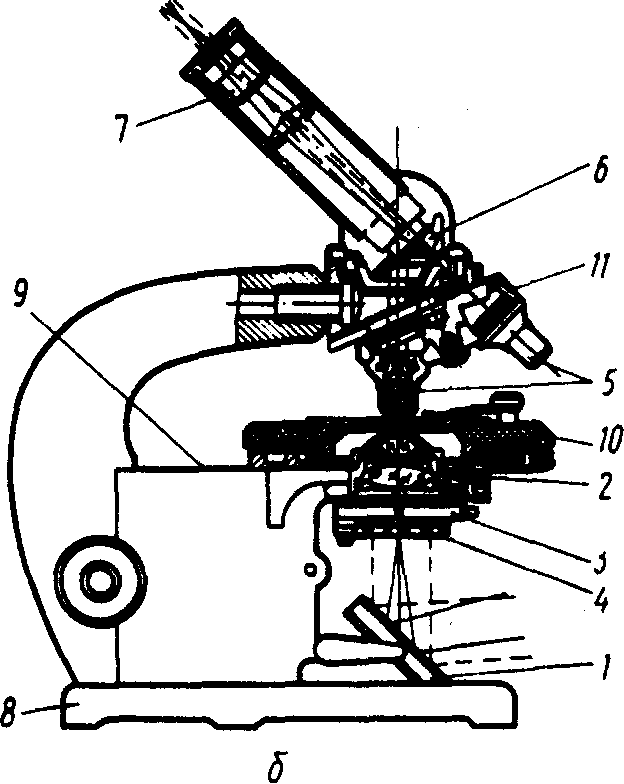
Рис. 2.2. Схема біологічного мікроскопа МБР-1

Механічна система мікроскопа складається з масивної підставки 8, тубусоутримувача, коробки з мікрометричним механізмом 9 для переміщення тубуса і предметного столика 10, на якому укріплені пружини, що притискають препарат до предметного столика.

Порядок і рекомендації щодо виконання роботи, оформлення й обробка результатів експерименту

1. Визначення ціни поділки окулярно-гвинтового мікрометра. Покласти на предметний столик камеру Горяєва. Одержати чітке зображення камери в окулярі мікроскопа. Повертаючи предметний столик, домогтися того, щоб вертикальні сторони клітин камери Горяєва були паралельні рискам шкали окулярно-гвинтового мікрометра. Обертаючи барабан мікрогвинта, встановити перехрестя окулярно-гвинтового мікрометра на вертикальну сторону якоїсь клітини камери Горяєва. Зняти показання п₁ окулярного мікрометра. Перемістити перехрестя на N клітин камери Горяєва, сполучити його з вертикальною стороною N-ї клітини. Зняти показання п₂ окулярно-гвинтового мікрометра. Визначити ціну поділки δ окулярно-гвинтового мікрометра δ = aN/(n₂ –n₁), де а - розмір сторони клітини камери Горяєва. Визначити ціну поділки δ окулярно-гвинтового мікрометра ще декілька разів, переміщуючи перехрестя щоразу на різне число N клітин камери Горяєва..

Знайти середнє значення ціни поділки окулярно-гвинтового мікрометра.

Результати вимірів і обчислень занести в табл. 2.1. Визначити похибку Δδ виміру ціни поділки окулярно-гвинтового мікрометра з довірчою вірогідністю α = 0,95.

2. Визначити розміри еритроцитів крові. Покласти на предметний столик мікроскопа гістологічний препарат крові.

Одержати чітке зображення еритроцитів в окулярі мікроскопа.

Сполучити перехрестя окулярно-гвинтового мікрометра з одним з країв еритроцита і зняти показання т₁ окулярного мікрометра.

Сполучити перехрестя з іншим краєм еритроцита, і зняти показання m₂ . Визначити розмір l=(m₂–т₁)δ еритроцита.

Зробити вимір розмірів для трьох різних еритроцитів. Результати вимірів і обчислень занести в табл. 2.2. Визначити похибку Δl виміру розміру еритроцита з довірчою вірогідністю α= 0,95.

Таблиця 2.1

N	а, мм	nІ	n2	n1-n2	<δ>, мм

Таблиця 2.2

<δ>, мм	m1	m2	m1 – m2	l,мм

3. Визначити концентрації еритроцитів і лейкоцитів у препаратах крові за допомогою камери Горяєва (рис.2.3).

Підрахунок червоних і білих тілець. Підрахунок проводиться в лічильних камерах. Лічильна камера являє собою скляну пластинку з невеличким поглибленням у центрі, куди поміщають розведену кров. На дні цього поглиблення розміщена сітка визначеного розміру. Між дном поглиблення і покривним склом висота (або глибина камери) дорівнює 0,1 мм. Кров'яні тільця осідають на дно камери, на сітку і рахуються. Порахована площа сітки, глибина камери і розведення крові відомі, і тому може бути вирахувана кількість кров'яних тілець в 1мм³ крові. Площа сітки Горяєва дорів­нює 9 мм² і містить 1515 великих квадра­тів різноманітних рисунків. 25 квадратів розділені на 16 маленьких квадратиків. У сітці є порожні квадрати, зібрані в групи, по 4 квадрати кожна. Усього таких груп у сітці – 25 (55), що містять 100 великих порожніх квадратів.

Контрольні запитання

1. Які формені елементи крові Ви знаєте?

2. Побудувати зображення предмета в мікроскопі.

3. Записати формулу для збільшення мікроскопа.

4. Записати формулу для розрізнення мікроскопа.

5. Як проводиться визначення концентрацій еритроцитів та лейкоцитів у препаратах крові за допомогою камери Горяєва?

Лабораторна робота 3

ВИЗНАЧЕННЯ В’ЯЗКОСТІ БІОЛОГІЧНИХ РІДИН ВІСКОЗИМЕТРОМ

Мета та основні завдання роботи: дослідження залежності в’язкості біологічних рідин від температури і концентрації; ознайомлення з роботою віскозиметра.

Обладнання, прилади і матеріали: віскозиметр, термометр, секундомір, набір біологічних рідин (розчин гліцерину, сольовий розчин, цукровий розчин, дистильована вода та ін).

Основні теоретичні відомості

У ході фізіологічних реакції системи кровообігу щільність крові змінюється менше ніж на десяті долі відсотка, тобто кров є практично нестисливою рідиною ( = 1,052 1,064 кг/м³).

В’язкість суцільної крові залежить від швидкості зсуву в діапазоні (0,1 - 120) с^-1, тоді як плазма і сироватка мають у стаціонарних умовах постійну в’язкість при усіх швидкостях зсуву.

Для суспензії, що містить менше 5% еритроцитів, виявляються властивості ньютонівської рідини. А при концентраціях еритроцитів більш ніж 10% виявляються властивості неньютонівської рідини (залежність від швидкості зсуву потоку). При течії реальних рідин прошарки, що рухаються з різними швидкостями, постійно обмінюються молекулами.

Молекули, що потрапляють із повільних прошарків у швидкі, мають меншу складову імпульсу mv направленого руху (рис. 4.1), у результаті чого гальмують швидкий прошарок. Молекули, переходячи зі швидкого прошарку в повільний, приносять із собою більшу складову імпульсу m(v+dv) і тим самим прискорюють повільний прошарок. Зміна імпульсу направленого руху на поверхні поділу прошарків обумовлює існування на ній сили, що спрямована проти руху рідини (газу) і називається силою внутрішнього тертя.

У випадку сталої ламінарної (без вихорів) течії в’язкої рідини має місце закон Ньютона: сила внутрішнього тертя F між двома прошарками прямо пропорційна площі їх дотику S і градієнту швидкості dv/dz (рис. 4.1)

F = . (4.1 )

Градієнт швидкості dv/dz характеризує зміну швидкості направленого руху на одиницю довжини в напрямку, перпендикулярному до поверхні тертя прошарків рідини. Величина  називається коефіцієнтом внутрішнього тертя або коефіцієнтом динамічної в’язкості. (Величина, обернена цьому коефіцієнту  = 1/, називається текучістю рідини). Прийнявши у формулі (4.1) dv/dz = 1 і S = 1, одержуємо, що F = , тобто коефіцієнт динамічної в’язкості є фізична величина, що чисельно дорівнює силі внутрішнього тертя між двома прошарками рідини одиничної площі при градієнті швидкості прошарків, що дорівнює одиниці. У системі СІ одиниця виміру в’язкості [] = кг м^-1 с^-1. Поряд із коефіцієнтом динамічної в’язкості вживається коефіцієнт кінематичної в’язкості (v = /, де  – щільність рідини),

34

34

Коефіцієнт динамічної в’язкості залежить від природи рідини і температури. Очевидно рідина буде тим менш в’язкою (і тим більш текучою), чим частіше молекули змінюють свої положення рівноваги, тобто чим менше час «осідлості» молекул . Тому можна припустити, що коефіцієнт динамічної в’язкості  пропорційний . Але час «осідлості»  залежить від температури за експоненційним законом. Отже, аналогічна температурна залежність є і для коефіцієнта динамічної в’язкості:

. (4.2)

Коефіцієнт _о слабко залежить від температури, він залежить від молекулярних параметрів рідини. Зокрема, для води отримаємо такий вираз:

,

д

27

е D – діаметр молекули;  – відстань між молекулами. (Для води можна прийняти D    3,5*10^-10м).

Закон плину в’язкої рідини в трубці. Нехай є циліндрична трубка довжиною АВ = l і радіусом R (рис. 4.2), Р_B і Р_A – тиск рідини

в поперечних перетинах В і А. Залежність швидкості v від r виявляється параболічною:

де Р = Р_А – Р_В, r – відстань елемента рідини від вісі трубки.

Пропускна здатність трубки D дорівнює

, або .

Це закон Пуазейля, справедливий для нетурбулентного потоку.

Класифікація рідин. Коефіцієнт в’язкості, навіть вимірюваний при фіксованій температурі, ще не є достатньою характеристикою рідини (виняток складає окремий випадок ньютонівскої рідини). Насправді  звичайно залежить від напруги зсуву  = F/S. Для класифікації рідин використовують так звані реологічні характеристики, тобто залежності  = F/S  від градієнта швидкості dv/dr (або від кутової швидкості обертання  за методом Куетта). Простіше усього подавати ці залежності графічно (рис. 4.3).

Розрізняють такі випадки:

1)  В’язкість не залежить від градієнта швидкості (ньютонівська рідина).

2)  В’язкість зменшується зі збільшенням градієнта швидкості (псевдопластична речовина).

3)  В’язкість зростає зі збільшенням градієнта (ділатантна речовина).

4 )  Існує межа текучості ₀ = (F/S)_о, іншими словами, якесь критичне значення напруги зсуву, при якому речовина стає текучою

(пластична речовина); коли зазначена властивість при підвищенні температури стає більш вираженою (або починає виявлятися), говорять про термопластичність.

30

5)  В’язкість зменшується при тривалому обертанні, але через

визначений час після зупинки повертається до початкового значення. У цьому випадку говорять про тиксотропну речовину. Тиксотропні рідини називають ще рідинами Бінгама.

6)  В’язкість, навпроти, зростає, а потім відновлює своє вихідне значення; у цьому випадку говорять про реопексну речовину.

Останні три категорії рідин мають деяку жорсткість.

Часто уживані визначення і формули. Якщо  – вимірюваний коефіцієнт в’язкості зразка, а ₀ – коефіцієнт в’язкості деякої еталонної речовини, то величина _від = /₀ називається відносною в’язкістю. Питома в’язкість – це величина _пит=(-₀)/₀=_від – 1. Величина, обернена коефіцієнту в’язкості, називається текучістю.

При вивченні властивостей розчинів залежно від концентрації розчиненої речовини іноді вводять характеристичну в’язкість

.

У випадку достатньо розведених розчинів можна використовувати:

– формулу Ейнштейна для сферичних частинок;

– формулу Кунітца для асиметричних частинок. Тут Ф – об'ємна частка розчиненої речовини (рис. 4.4).

Якщо n молекул, кожна з яких має об’єм V_M, знаходяться в розчині об’ємом V, то Ф =nV_М/V; якщо n відомо, можна обчислити об’єм, що займає одна молекула. Ця формула використовується для знаходження ступеня гідратації іонів у водяних розчинах. Для розчинів полімерів було отримане співвідношення, що зв'язує характеристичну в’язкість, концентрацію і молекулярну масу М розчиненої речовини:

де К - константа, характерна для даного полімеру.

Вимірювання коефіцієнта в'язкості є зручним засобом спостереження за розщеп-ленням ДНК нуклеазами. Дійсно, з розщепленням ДНК її молекулярна маса зменшується і, отже, зменшується коефіцієнт в’язкості.

Зменшення в’язкості рідини з ростом температури описується в першому наближенні співвідношенням (4.2).

В’язкість рідин зростає зі збільшенням тиску. Виняток складає вода (у всякому разі, при кімнатній температурі), в якій в’язкість спочатку падає і тільки потім починає рости, як у звичайних рідин.

Межі придатності класичних законів. Фізико-хімічні методи частіше усього використовуються для вивчення гомогенних рідин, тобто рідин, макроскопічні властивості котрих, і зокрема склад, однакові у всіх точках. Введення відповідних поправок (Ейнштейна, Кунітца) дозволяє застосо­вувати класичні закони і до розведених однорідних суспензій.

Закони течії крові по кровоносних судинах істотно складніші. Кров не є гомогенною суспензією, вона містить множину так званих формених елементів (еритроцитів, лейкоцитів і т.д.).

Визначимо гематокрит як відношення об’єму, що займають еритроцити, до об’єму плазми. У нормі цей параметр для крові людини дорівнює 0,4. При даній температурі ( 37,5 ^oС) в’язкість крові зростає з ростом гематокрита.

В’язкість крові зростає як із ростом кількості еритроцитів, так і зі збільшенням їхнього об’єму, наприклад, коли в крові підвищується вміст СО₂. Звідси зрозуміло, що венозна кров менш текуча, ніж артеріальна. У кровоносних судинах відбувається орієнтація еритроцитів, а також їхня деформація (у капілярах). Крім того, спостерігається агрегація формених елементів (особливо еритроцитів) і радіальна неоднорідність кров'яного потоку; щільність еритроцитів зростає з наближенням до вісі кровоносної судини, що призводить до уплощення профілю швидкості, що є параболічним у випадку ньютонівської рідини. У прилеглих до стінки судини областях кров є більш розбавленою, що, безсумнівно, полегшує дихальний обмін з омиваною тканиною.

Цей збідненний еритроцитами прошарок крові товщиною приблизно 1 мкм є найменш в’язким (_від  2 замість 3,3), у результаті кров тут рухається швидше. У дрібних судинах товщина пристінного прошарку складає істотну частину поперечного перетину, і, отже, гематокрит у капілярах помітно менший, ніж у великих судинах. Гематокрит є дуже важливою характеристикою, тому що від нього залежить текучість крові, тканинний обмін і продуктивність серця (остання зростає при збільшенні в’язкості крові).

Зауважимо далі, що стінки кровоносних судин еластичні, а не жорсткі, як у скляної трубки.