1. 4. Алгебри перемикальних функцій

Аналітичний спосіб подання перемикальних функцій посідає особливе місце в теорії перемикальних функцій. Фактично всі перетворення над пе6ремикальними функціями, необхідні для синтезу та аналізу цифрових автоматів, здійснюються на аналітичному рівні.

Для побудови логічних схем на практиці може бути застосований певний функціональний елементний базис.

Функціональний елементний базис – це сукупність типів функціональних елементів, які можна використовувати для побудови схем.

Вміння представляти перемикальні функції у заданому елементному базисі має важливе практичне значення. Одна і та сама функція може бути представлена різними формулами. Кожній формулі відповідає своя суперпозиція перемикальних функцій, а кожній суперпозиції, у свою чергу, відповідає логічна схема з певною складністю.

Очевидно, серед схем, які реалізують дану функцію в певному елементному базисі, є найпростіша. Пошук логічної формули, відповідної даній схемі, має велике практичне значення. Відповідні перетворення формул перемикальних функцій виконують на основі співвідношень алгебр перемикальних функцій.

1. 4. 1. Алгебра Буля

Алгебра визначена на змінних. Для перетворення аргументів в алгебрі Буля використовуються функції І, АБО та НЕ. Система перемикальних функцій відповідно має вигляд

;

;

.

Аксіоми алгебри Буля:

; ; .

; ;

; ;

; ;

Основні закони (властивості) алгебри Буля.

1. Закон комутативності (переставний закон): ;

.

2. Закон асоціативності (сполучний закон): ;

.

3. Закон дистрибутивності (розподільний закон):

;

.

З практичного погляду закон комутативності означає, що всі входи елементів І та АБО мають однакові функціональні властивості. Тому різні вхідні сигнали можна подавати на будь-які входи елементів.

Із комутативності і асоціативності диз’юнкції витікає, що диз’юнкція кількох змінних може виконуватися послідовно, причому порядок взяття диз’юнкції не впливає на результат.

Таким чином, диз’юнкція сукупності змінних може бути виражена співвідношенням

Аналогічно і для кон’юнкції

Властивість асоціативності дозволяє за рахунок декомпозиції (каскадування) елементів реалізувати функції І та АБО від будь-якої кількості аргументів на основі елементів з меншою кількістю входів.

Закон дистрибутивності визначає правило винесення за дужки перемінної. Завдяки цьому у деяких випадках можна зменшувати складність логічних схем.

Зв’язок між функціями І, АБО, І-НЕ, АБО-НЕ встановлюється за допомогою правил (теорем) де Моргана:

;

; (1. 2)

або

;

.

Теореми де Моргана для декількох змінних мають вигляд:

;

.

З наведених співвідношень видно, що функції І та АБО мають однакові властивості. Такі функції називають дуальними.

Таким чином, користуючись теоремами де Моргана, можна виражати кон’юнкцію через диз’юнкцію і заперечення, а диз’юнкцію − через кон’юнкцію і заперечення.

Всі вищенаведені властивості дозволяють поводитися з логічними функціями, як із числами, і при аналізі складних логічних виразів користуватися алгебраїчними методами перетворення їх до вигляду, зручного для аналізу. Однак, перетворення формул булевих функцій застосуванням тільки властивостей і аксіом булевої алгебри та правил де Моргана малоефективне. Для спрощення формул використовують цілу низку співвідношень. Наведемо деякі з них:

, ;

;

, .

Приклад. Спростити логічну функцію

.

Застосуємо теорему де Моргана до диз’юнкцій із запереченням:

).

Розкриваючи дужки, отримаємо

,

оскільки .

Перетворимо іншу частину функції. Розкриваючи дужки, отримаємо

,

так як у другому члені є добуток , який обертає його в нуль.

Підставивши перетворені вирази окремих членів функції у вихідну формулу, отримаємо

.

Застосовуючи формулу склеювання до першого і другого кон’юнктивних членів, а формулу поглинання до третього і п’ятого кон’юнктивних членів, можна спростити цей вираз до вигляду

.

Застосовуючи формулу поглинання до першого і третього кон’юнктивних членів, отримаємо

Для доведення логічних співвідношень використовують два способи: порівняння таблиць істинності лівої та правої частини співвідношення, а також застосування аксіом та теорем для приведення лівої та правої частини співвідношення до одного вигляду.

Приклад. Довести справедливість співвідношення властивості дистрибутивності в алгебрі Буля

.

Спочатку доведемо справедливість даного співвідношення способом порівняння таблиць істинності його лівої та правої частини. Для цього побудуємо таблицю, в якій поетапно визначимо значення всіх членів лівої та правої частини співвідношення дистрибутивності для всіх наборів аргументів (табл. 1. 7). У лівій частині таблиці наведемо всі можливі набори аргументів. Для зручності позначимо стовпці таблиці цифрами. Спочатку заповнимо

Таблиця 1. 7

1	2	3	4	5	6
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 0 1 0 0 0 1	0 0 0 1 1 1 1 1	0 0 1 1 1 1 1 1	0 1 0 1 1 1 1 1	0 0 0 1 1 1 1 1

стовпці 2 і 3, а потім – стовпці 4, 5 і 6.

У стовпцях 3 і 6, що відповідають лівій і правій частині співвідношення дистрибутивності, значення збігаються для всіх наборів аргументів, що і треба було довести.

Далі доведемо справедливість даного співвідношення дистрибутивності за допомогою аксіом і теорем алгебри Буля. Для цього перетворимо праву частину співвідношення:

.

Вираз, отриманий у результаті перетворень, дорівнює лівій частині заданого співвідношення. Таким чином. Справедливість заданого співвідношення закону дистрибутивності доведено.

Канонічні форми алгебри Буля

Розглянемо універсальні (канонічні) форми перемикальних функцій, які дають можливість одержати аналітичну форму безпосередньо по таблиці істинності для довільної булевої функції. Ця форма потім може бути спрощена. Оскільки між множиною аналітичних представлень і множиною схем, що реалізують булеву функцію, існує взаємно-однозначна відповідність, відшукання канонічної форми подання булевої функції є початковим етапом синтезу схеми, яка її реалізує.

Оскільки в алгебрі Буля функції І та АБО є дуальними, то існують дві канонічні форми булевих функцій:

− довершена диз’юнктивна нормальна форма (ДДНФ);

− довершена кон’юнктивна нормальна форма (ДКНФ).

Базовим поняттям для побудови ДДНФ є конституента одиниці.

Конституента одиниці – це функція, що приймає одиничне значення тільки на одному наборі аргументів.

Конституента одиниці записується як логічний добуток різних змінних (із запереченням або без заперечення). Наприклад, − елементарний логічний добуток, який є конституентою одиниці змінних , , , , приймає значення одиниці на єдиному наборі 1010.

Окремим випадком конституенти одиниці є логічна функція кон’юнкції.

Кон’юнкцією аргументів називається перемикальна функція типу конституенти одиниці, яка дорівнює одиниці тільки коли всі аргументи дорівнюють одиниці (тобто при наборі 11…1) і дорівнює нулю у всіх інших випадках (тобто коли хоча б один із аргументів дорівнює 0)

.

Будь-яка послідовність аргументів, об’єднаних однією операцією, називається термом.

Аналітичний запис конституенти одиниці є кон’юнктивним термом (мінтермом) -рангу.

Змінна (із запереченням або без заперечення) в термі називається буквою.

Кількість букв в термі називається рангом терма.

Так як диз’юнкція дорівнює одиниці, якщо хоча б одна із змінних приймає значення одиниці, то можна легко виразити будь-яку булеву функцію як диз’юнкцію конституент одиниці, які відповідають тим наборам, на яких функція дорівнює одиниці.

Таким чином, ДДНФ – це диз’юнкція конституент одиниці , що відповідають наборам, на яких функція приймає одиничні значення, тобто

, ( 1. 3)

де − - й набір; {0, 1} − значення функції на - му наборі.

Приклад. Знайти ДДНФ для перемикальних функцій, заданих таблицею істинності (табл. 1. 8).

Таблиця 1. 8

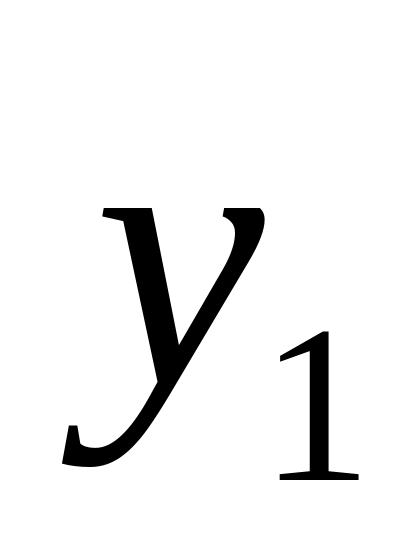
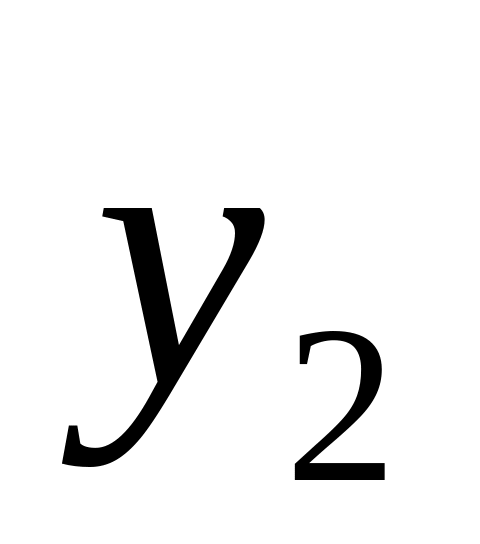
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 1 0 1 1 0 1	1 1 0 0 1 0 1 0	0 1 0 1 0 1 1 1

ДДНФ функцій , та будуть мати вигляд:

;

;

.

Зауваження. Часто для спрощення запису функцій замість повного переліку термів застосовують номери наборів, де функція приймає одиничне значення. Така форма запису називається цифровою.

Отримані ДДНФ можуть бути подані у цифровому вигляді, де конституента одиниці задається номером набору.

; ; .

ДКНФ будується аналогічно ДДНФ. Базовим поняттям для побудови ДКНФ є конститунета нуля.

Конституента нуля – це функція, що приймає нульове значення тільки на одному наборі.

Окремим випадком конституенти нуля є перемикальна функція диз’юнкції.

Диз’юнкцією аргументів називається логічна функція типу конституенти нуля, яка приймає нульове значення тільки тоді, коли всі її аргументи дорівнюють нулю, тобто при наборі 00…0. У всіх інших випадках, тобто коли хоча б один із аргументів дорівнює одиниці, функція приймає одиничне значення

Таким чином, конституента нуля може бути записана у вигляді диз’юнктивного терму -го рангу. Нульовому значенню аргументу в термі відповідає буква без заперечення, а одиничному – із запереченням. Наприклад, набору 0110 змінних , , , відповідає конституента нуля .

Аналітичний запис конституенти нуля є диз’юнктивним термом (макстермом) -рангу.

Довершена кон’юнктивна нормальна форма (ДКНФ) – це кон’юнкція конституент нуля, тобто

, (1. 4)

де − -й набір; {0, 1} − значення функції на - у наборі.

Приклад. Знайти ДКНФ перемикальних функцій , та , заданих таблицею істинності (табл. 1. 8)

Згідно з виразом (1. 4) ДКНФ функцій будуть мати вигляд:

;

;

.

У цифровому вигляді одержані перемикальні функції можна записати так:

; ; .

Сумарна кількість букв у аналітичному запису перемикальної функції називається ціною форми. Взагалі ціна ДДНФ і ДКНФ може відрізнятися.

Якщо немає обмежень на кількість входів логічних елементів, то логічні схеми, які реалізують нормальні форми будь-якої алгебри, завжди мають два рівні. Вхідний сигнал у таких схемах проходить до виходу через ланцюжок, що має два елементи.

Приклад. Побудувати логічну схему, що реалізує перемикальну функцію у ДДНФ і ДКНФ (табл. 1.8).

Комбінаційна схема, зображена на рис. 1. 4, а реалізує ДДНФ перемикальної функції, а комбінаційна схема на рис. 1. 4, б – ДКНФ перемикальної функції .

Отримані комбінаційні схеми мають два логічних рівні. Комбінаційні схеми відрізняються за складністю.

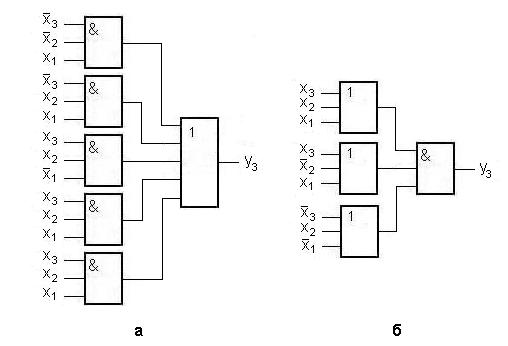
Рис. 1. 4. Комбінаційні схеми: а – для ДДНФ функції; б – для її ДКНФ

Способи перетворення нормальних форм у довершені

нормальні форми

Крім канонічних форм (ДДНФ і ДКНФ) існують і нормальні форми перемикальних функцій: диз’юнктивна нормальна форма (ДНФ) і кон’юнктивна нормальна форма (КНФ). Довершені нормальні форми (ДДНФ і ДКНФ) відрізняються від нормальних форм тим, що завжди містять терми тільки максимального рангу і дають однозначне представлення функції.

Довільну диз’юнктивну нормальну форму можна перетворити наступним чином.

Допустимо, що в терм нормальної форми ДНФ перемикальної функції не входить змінна . Тоді одержати терм максимального рангу можна із виразу

. (1. 5)

Приклад. Перемикальну функцію, задану в ДНФ

, перетворити в ДДНФ.

Для отримання ДДНФ заданої функції перетворимо кожний її терм згідно з виразом (1. 5).

.

Довільна кон’юнктивна нормальна форма може бути перетворена в ДКНФ так.

Допустимо, що в диз’юнктивний терм нормальної кон’юнктивної форми перемикальної функції не входить змінна . Тоді одержати терм максимального рангу можна наступним перетворенням

. (1. 6)

Приклад. Перетворити в ДКНФ перемикальну функцію

.

Застосувавши правило перетворення (1. 6) до першого і другого термів функції, після спрощень одержимо

.