4. 2. Синтез мікропрограмних автоматів.

При описі функціонування різних засобів обчислювальної техніки досить часто використовується їх подання у вигляді сукупності керуючого і операційного автоматів (рис. 4. 10), який реалізує певну систему операцій. Кожній операції відповідає послідовність операторів (мікрооперацій). А кожному оператору відповідає сукупність структурних сигналів автомата із множини .

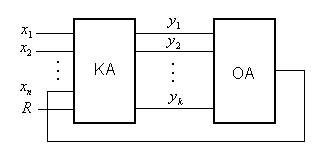
Рис. 4. 5. Загальна структура засобів обчислювальної техніки

Керуючий автомат (КА) може розглядатися як пристрій, який реалізує алгоритм функціонування, що визначає порядок виконання окремих операції чи процедур з керування деяким об’єктом – операційним автоматом (ОА).

Задача керуючого автомата полягає у виробленні розподіленої в часі послідовності вихідних (керуючих) сигналів, під дією яких в операційному автоматі здійснюється певна операція.

Елементарний неподільний акт обробки інформації в операційному автоматі, що відбувається протягом одного моменту автономного часу (одного такта роботи автомата), називається мікрооперацією. Наприклад, „зсув інформації”, „+1”, „інвертування змінної”, тощо.

Якщо в операційному автоматі одночасно реалізується кілька

мікрооперацій, то така множина мікрооперацій називається мікрокомандою. Бувають випадки, коли множина мікрооперацій , що утворює мікрокоманду, порожня. Реалізація такої мікрокоманди в ОА рівнозначна відсутності виконання будь-яких елементарних операцій. В синхронних дискретних пристроях порожня мікрокоманда інтерпретується як пропуск такту, коли від керуючого автомата ніякі сигнали не надходять на операційний автомат.

Мікро операції збуджуються вихідними сигналами КА, а їх послідовність в часі визначається функціями переходу керуючого автомата.

Сукупність мікрокоманд і функцій переходу утворює мікропрограму. Таким чином, для описання мікропрограми необхідно задати множину мікрокоманд і функцій переходу, що визначають порядок їх виконання.

Послідовність сигналів, що виробляються керуючим автоматом, залежить від стану самого КА і зовнішнього сигналу , який може надходити ззовні, наприклад, від іншого КА або від людини.

Як систему КА – ОА можна розглядати звичайну ЕОМ, в котрій КА являється процесор, а операційним пристроєм – запам’ятовуючий пристрій (ЗП). Якщо ЕОМ включена в цикл керування яким-небудь об’єктом, то КА такої системи являється уже вся ЕОМ.

При необхідності детальнішого розгляду функціонування самого процесора ЕОМ у вигляді системи „КА – ОА” як КА розглядається центральний блок (пристрій) керування (ЦБК), а як ОА – арифметико- логічний пристрій (АЛП).

Синтез цифрових автоматів складається з етапів абстрактного та структурного синтезу.

Абстрактний синтез автоматів з пам’яттю

Результатом абстрактного синтезу автомата є його формальний опис сукупністю п’яти об’єктів , де , − вхідний алфавіт автомата; , − вихідний алфавіт автомата; , − алфавіт станів автомата; − функція переходів автомата , яка задає відображення множин , тобто яка ставить у відповідність будь-якій парі елементів декартового добутку множин елемент ; − функція виходів автомата, яка задає відображення , або . Отже, функція переходів визначає спосіб переходу автомата із одного стану в інший, а функція виходів – формування вихідних сигналів.

Структурний синтез дозволяє одержати логічну схему автомата в заданому елементному базисі.

Абстрактний синтез складається з таких етапів:

- формування вхідного та вихідного алфавітів;

- складання алгоритму функціонування автомата;

- формування алфавіту внутрішніх станів автомата;

- визначення функцій переходів і виходів за допомогою графа або відповідних таблиць.

Вхідний алфавіт формується на основі вивчення зовнішніх для автомата сигналів, які можуть розглядати як логічні умови, що змінюють режим функціонування автомата. Різні комбінації вхідних сигналів розглядаються як букви вхідного алфавіту.

Автомат, як правило, забезпечує управління деяким операційним пристроєм, що перетворює цифрову інформацію шляхом виконання певних операторів. Кожному оператору відповідає певний набір управляючих сигналів, який на абстрактному рівні розглядається як певна буква вихідного алфавіту управляючого автомата.

Для отримання алгоритму функціонування автомата необхідно чітко представляти спосіб перетворення інформації.

Для опису алгоритмів функціонування цифрового автомата зручно використовувати графічні схеми алгоритмів (ГСА).

Граф схемою алгоритму називається орієнтований зв’язаний граф, який має одну початкову вершину („Початок“), одну кінцеву вершину („Кінець“) і довільну кінцеву множину умовних і операторних вершин.

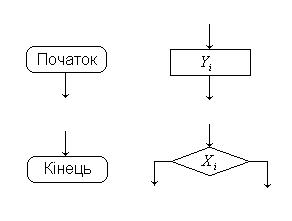
ГСА складається з вершин чотирьох типів (рис. 4. 1). Алгоритм починається з вершини „Початок“ і закінчується вершиною „Кінець“. Букви вихідного алфавіту (вихідні сигнали, оператори) записують в операторні вершини, а букви вхідного алфавіту (вхідні сигнали, логічні умови) розміщують у логічні (умовні) вершини.

Кожна вершина ГСА, крім вершини „Початок“, має по одному входу. Вершина „Початок“ і кожна операторна вершина, крім вершини „Кінець“ мають по одному виходу. Кожна умовна вершина має два виходи, позначені символами „Так“ і „Ні“ (замість цих символів можуть бути використані цифри 1 і 0 відповідно).

ГСА має задовольняти наступним умовам: 1. Входи і виходи

Рис. 4. 6. Умовні позначення вершин з’єднуються один з одним за

вершин ГСА допомогою дуг, направлених завжди

від виходу до входу;

2. Кожний вихід з’єднується тільки з одним входом;

3. Будь-який вхід з’єднується принаймні з одним виходом;

4. Будь-яка вершина ГСА лежить принаймні на одному шляху із вершини „Початок“ до вершини „Кінець“;

5. Один із виходів умовної вершини може з’єднуватися із її входом, що не допустимо для операторної вершини;

6. В кожній умовній вершині записується логічна умова (вхідний сигнал) із множини логічних умов. Дозволяється в різних умовних вершинах записувати однакові логічні умови;

7. В кожній операторній вершині записується оператор, який є вихідним сигналом або сукупністю вихідних сигналів керуючого автомата. Дозволяється в різних операторних вершинах записувати однакові оператори.

Після створення ГСА процес побудови графа автомата і визначення алфавіту внутрішніх станів можна формалізувати. У зв’язку з цим ГСА, як і граф, можна вважати формальним описом абстрактного автомата.

Для побудови графа автомата виконується розмітка станів автомата на ГСА. Способи розмітки автоматів Мура і Мілі відрізняються.

Розмітка станів автомата Мілі здійснюється таким чином:

− символом позначається вхід наступної за початковою вершини (логічної або операторної), а також вхід кінцевої вершини (якщо автомат реалізує циклічний процес);

− входи всіх вершин, наступних за операторними, позначаються символами .

Розмітка станів автомата Мура здійснюється за такими правилами:

− символом позначаються початкова і кінцева вершини;

− всі операторні вершини позначаються різними символами .

У результаті розмітки ГСА визначається алфавіт внутрішніх станів.

Побудова графа автомата виконується на основі розміченої ГСА. Число вершин графа дорівнює числу станів автомата. Кожному переходу автомата з одного стану в інший відповідає дуга графа. Дузі приписується умова, за якої здійснюється перехід автомата з одного стану в інший. Для автомата Мілі вихідні сигнали приписують дугам, а для автомата Мура – розміщують у вершинах графа. Приклади графів абстрактних автоматів наведені на рис. 2. 3.

Структурний синтез автоматів з пам’яттю

Результати абстрактного синтезу автомата можуть розглядатися як вихідні дані для структурного синтезу. Під час проектування реальних систем на етапах структурного синтезу може виникнути необхідність корегування результатів абстрактного синтезу (наприклад, ГСА та графа автомата). Це може зумовлюватися необхідністю усунення ризиків збою, врахуванням тривалості структурних сигналів, елементної бази тощо. Таке корегування може привести до введення нових вершин і дуг в граф автомата. Таким чином, множина станів абстрактного автомата може відрізнятися від множини станів структурного автомата .

Структурний синтез синхронного автомата включає такі етапи:

- складання списку структурних вихідних сигналів, що відповідають кожній букві вихідного алфавіту абстрактного автомата;

- визначення тривалості кожного вихідного структурного сигналу (в числі тактів) і періоду тактуючих сигналів автомата;

- одержання закодованої ГСА структурного автомата, тобто корегування ГСА абстрактного автомата, якщо сигнали мають різну тривалість;

- розмітка ГСА структурного автомата;

- складання графа структурного автомата;

- кодування станів структурного автомата;

- вибір елементів пам’яті і структурно повної системи логічних елементів (якщо вони не задані);

- складання структурної таблиці автомата;

- одержання МДНФ функцій збудження тригерів і керуючих сигналів (виходів автомата);

- вираження функцій збудження тригерів і керуючих сигналів в операторній формі;

- побудова схеми керуючого автомата.

Якщо всі вихідні сигнали структурного автомата мають однакову тривалість, то після першого пункту на графі абстрактного автомата замінюють абстрактні терміни структурними і переходять до кодування станів структурного автомата.

Нехай на етапі абстрактного синтезу одержана ГСА в абстрактних термінах (рис. 4. 7).

Відповідність абстрактних та структурних сигналів визначається особливостями керування операційним пристроєм. Нехай за рахунок аналізу пристрою одержана відповідність зазначених сигналів (табл. 4. 11).

На практиці необхідна тривалість керуючих сигналів визначається з урахуванням затримок в елементах операційного пристрою. Виходячи з цього обирається період тактуючих сигналів. При цьому величина має бути не менше часу переключення автомата з одного стану в інший.

Як видно з табл. 4. 11, керуючі сигнали і повинні мати тривалість , а інші − . Подвійна тривалість сигналів може бути забезпечена, наприклад, введенням у ГСА додаткових операторних вершин з керуючими сигналами, тривалість яких перевищує .

Для одержання ГСА автомата в структурних термінах (структурної ГСА) складаємо таблицю позначень логічних умов (табл. 5) і замінюємо абстрактні терміни в ГСА (рис. 7) на структурні. Оскільки управляючі сигнали та мають тривалість , то на структурній ГСА Рис. 8) вводимо додаткову операторну вершину 4, що відповідає цим управляючим сигналам.

На рис. 8 ГСА відзначена чотирма різними станами ( ). Таку саму кількість вершин має граф автомата Мілі, зображений на рис.9.

Кожному переходу автомата з одного стану в інший відповідає дуга графа. Дузі приписується логічна умова, за якої здійснюється перехід автомата з одного стану в інший, а також набір управляючих сигналів, що відповідають даному переходові. Якщо перехід безумовний, то замість умови проставляють „−“.

Кількість тригерів, необхідних для організації пам’яті автомата, визначається із співвідношення , де − число станів автомата. Кожному станові має відповідати одна визначена комбінація значень .

Для прикладу, що розглядається, вибираємо коди станів відповідно до табл. 6.

Для організації пам’яті використовуємо -тригери, а для побудови комбінаційних схем – елементи булевого базису.

Відзначимо, що спосіб кодування станів впливає на правильність формування управляючих сигналів і складність автомата. (це питання докладніше розглядатиметься в розділі 1. 4).

Структурна таблиця автомата складається за його графом. Кожен рядок (табл. 7) відповідає визначеному переходові автомата з одного стану в інший. У рядку записують вихідний стан, стан переходу, коди цих станів, значення логічних умов, що забезпечують перехід, необхідні значення управляючих сигналів і функцій збудження тригерів. Значення функції збудження тригерів визначають згідно з таблицею переходів тригера відповідного типу. В кожному рядку для -го тригера розглядаються переходи . Довільні значення управляючих сигналів (0 або 1) позначаються в структурній таблиці символом „−“. Довільні значення управляючих сигналів визначаються особливостями операційного пристрою. В даному випадку як приклад такі значення прийняті для сигналів .

На підставі структурної таблиці автомата визначаємо МДНФ функцій збудження тригерів і функцій управляючих сигналів. Аргументами функцій та є значення та у початковому стані.

Для отримання МДНФ функцій використовуємо діаграми Вейча (рис.10).

Після мінімізації одержимо функції:

;

;

;

;

;

;

.

Функціональна схема автомата зображена на рис. 11, де УПС − установлення початкового стану (активний рівень сигналу низький), − тактуючі сигнали.

Розглянемо приклад синтезу автомата Мура на - тригерах та елементах булевого базису.

Будемо вважати, що одержано таку саму ГСА структурного автомата, як у попередньому прикладі (рис. 7). Після розмітки станів за правилами автомата Мура структурна ГСА приймає вигляд, наведений на рис. 12, а граф автомата мура – як на рис. 13.

Кодування станів автомата Мура виконаємо аналогічно до розглянутого у прикладі автомата Мілі (табл. 7).

На основі графа складаємо структурну таблицю автомата Мура (табл. 8).

Вихідні сигнали в автоматі Мура залежать тільки від початкового стану і . Функції збудження тригерів, як і для автомата Мілі, залежать від початкового стану і вхідних сигналів.

На підставі структурної таблиці автомата визначаємо МДНФ функцій збудження тригерів і функцій управляючих сигналів, для чого використовуємо діаграми Вейча (рис. 14).

Після мінімізації одержимо функції:

;

;

;

;

;

;

.

Функціональна схема автомата показана на рис. 4.