ЛОГІЧНІ ОСНОВИ ЦИФРОВИХ АВТОМАТІВ

Розділ 1. Основи теорії перемикальних функцій

1.1. Подання інформації в цифровій обчислювальній техніці

1.2. Перемикальні функції і логічні схеми

Пристрій, що реалізує дії над двійковими числами, можна розглядати як функціональний перетворювач (ФП) або цифровий автомат (ЦА) з n входами і m виходами, на входи якого надходять вхідні двійкові числа, а на виходах утворюється результат перетворення теж у вигляді двійкового числа. двійкового числа на його виході утворюється вихідне двійкове число . Таким чином, значення вихідного числа визначається конкретним поєднанням значень всіх n розрядів вхідного двійкового числа, що називається двійковим набором. Кожному набору на вході ЦА будуть відповідати 0 чи 1 на відповідному виході.

Функція називається перемикальною, або логічною, якщо сама функція і кожен з її аргументів приймають значення тільки із множини {0, 1}.

Логічною основою цифрових автоматів є алгебра логіки – одна із основних частин математичної логіки. Дослідженням властивостей перемикальних функцій займається математична логіка. Для опису роботи цифрових автоматів застосовується математичний апарат алгебри логіки або алгебри перемикальних функцій.

Довільна перемикальна функція може бути задана різними способами, наприклад:

− словесним описом;

− матричним (табличним) способом;

− геометричним представленням;

− аналітичним виразом..

Наприклад, перемикальну функцію можна описати таким чином. Функція від аргументів , і приймає значення одиниці, якщо більшість її аргументів приймає нульові значення.

При матричному способі задану вище перемикальну функцію можна зобразити у вигляді таблиці істинності (табл. 1. 1), в лівій частині якої представлені всі можливі двійкові набори довжини n, а в правій вказується значення функції на цих наборах.

Набором називають упорядковану послідовність значень аргументів перемикальної функції.

Двійковий набір має довжину n, якщо він представлений n цифрами із множини {0, 1}. В табл. 1. 1 перелічені всі двійкові набори. Очевидно, що набір значень аргументів фактично є деяким двійковим числом. Між

Таблиця 1. 1

Номери наборів	Набори аргументів			Значення функції
0	0	0	0	1
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	0

двійковими наборами і двійковими числами існує взаємно однозначна відповідність. Отже, існує 2ⁿ різноманітних наборів двійкових змінних.

Кожний набір має свій номер, який збігається з кількісним еквівалентом двійкового числа. Наприклад, якщо набори впорядковуються у послідовності … , то номер набору визначається як

Таким чином, двійкові набори в таблиці істинності перемикальної функції можуть бути надані їх номерами.

Табличний спосіб подання перемикальної функції є наглядним і теоретично може бути застосований для запису функцій довільної кількості змінних. Для визначення функції не обов’язково задавати її значення на всіх наборах. Достатньо визначити всі набори, які перетворюють цю функцію в нуль, чи всі набори, що перетворюють її в одиницю.

Недоліком табличного способу подання перемикальних функцій є його громіздкість, яка зростає із збільшенням аргументів функції. Так, наприклад, таблиця істинності перемикальної функції 10 змінних буде містити 2¹⁰ = 1024 рядків. Деякого спрощення можна досягти, якщо при поданні функції багатьох змінних скористатися модифікованою таблицею істинності.

Розглянемо спосіб побудови такої таблиці істинності для функції змінних. Множина аргументів функції поділяється на дві підмножини:

Таблиця 1. 2

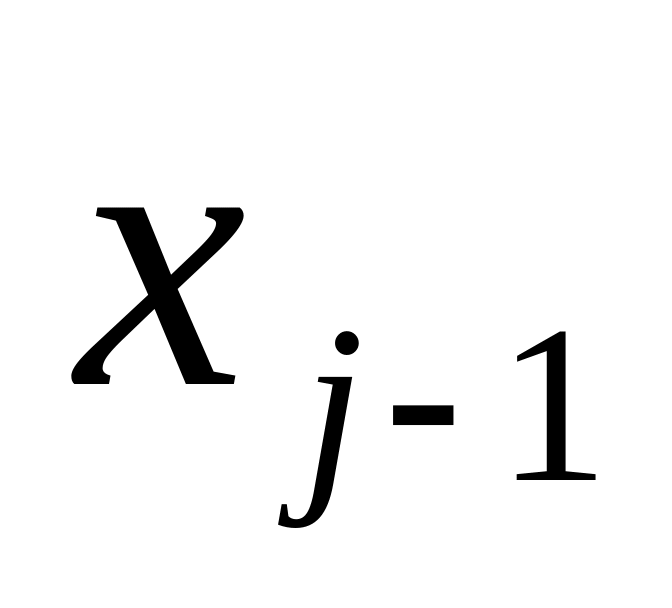
Набори аргументів …	Набори аргументів …
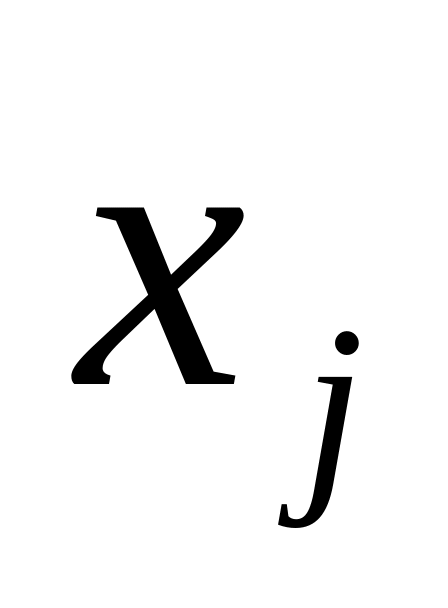
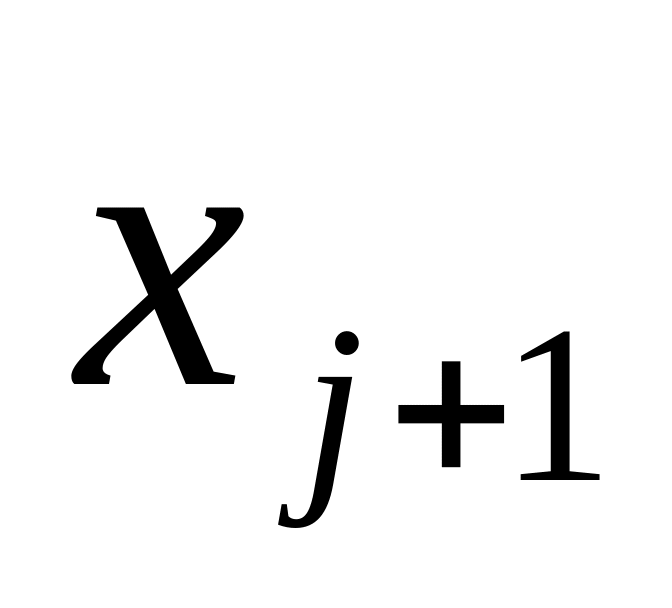	0 0 … 0	0 0 … 1	. . .	1 1 … 1
0 0 … 0
0 0 … 1
…
1 1 … 1

та . Змінними позначають рядки таблиці істинності, задаючи в кожному рядку значення відповідного двійкового набору довжиною ( ), а змінними − її стовпці, задаючи в кожному стовпці значення відповідного двійкового набору довжини ( ). Значення функції записується в клітинку на перетині відповідного рядка та стовпця (табл. 1.2). Модифікована таблиця істинності перемикальної функції 10 змінних буде мати 32 рядки і 32 стовпці. Таким чином, табличний спосіб подання перемикальних функцій є громіздким і практично придатний тільки для функцій з малим числом аргументів ( або 5).

При геометричному способі перемикальну функцію від аргументів можна задати -мірним кубом. В геометричному значенні кожний двійковий набір є -мірним вектором, який визначає точку -мірного простору. Виходячи із цього, вся множина наборів, на яких визначена функція від аргументів, зображається вершинами -мірного куба. Позначаючи точками вершини куба, в яких функція приймає одиничне (або нульове) значення, одержимо геометричне зображення функції. Наприклад, для перемикальної функції трьох аргументів, заданої у табл. 1. 1, геометричне зображення наведене на рис. 1. 1, в. Кількість вершин дорівнює кількості наборів. Точкою позначені набори, на яких функція має одиничне значення.

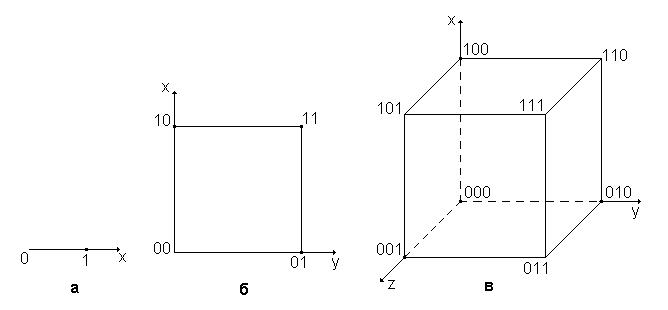
Рис. 1. 1. Геометричне зображення перемикальних функцій:

а – однієї змінної; б – двох змінних; в – трьох змінних

Геометричне подання перемикальної функції, як і табличне, також значно ускладнюється за збільшення кількості аргументів функції. Тому значно простіше виглядає аналітичний запис у вигляді формул.

При аналітичному способі перемикальна функція задається формулами, тобто аналітичними виразами, побудованими за допомогою логічних операцій різних алгебр перемикальних функцій, наприклад:

;

.

Одержання аналітичних форм перемикальних функцій у різних алгебр розглядається пізніше.

Розглянемо області визначення перемикальних функцій.

Як вже зазначалось, між двійковими наборами і двійковими числами існує взаємно однозначна відповідність. Отже, існує 2ⁿ різних наборів двійкових змінних.

Таким чином, областю визначення перемикальної функції n змінних при табличному способі подання є множина всіх можливих двійкових наборів довжини n, а при геометричному способі − множина всіх вершин n – мірного одиничного куба.

Перемикальну функцію, визначену на всіх своїх наборах, називають повністю визначеною. В табл. 1. 1 наведений приклад повністю визначеної перемикальної функції.

Перемикальну функцію n змінних називають неповністю визначеною чи частковою, якщо вона визначена не на всіх двійкових наборах довжини n.

Легко переконатися, що якщо перемикальна функція f не визначена на m наборах аргументів, то її довизначенням можна отримати 2^m різних повністю визначених функцій.

За наявності аргументів кількість різних наборів становить

.

Враховуючи, що на кожному наборі перемикальна функція може приймати два значення (0 або 1), за правилами комбінаторики одержимо загальну кількість перемикальних функцій:

.

Таким чином, за одного аргументу існують 4 перемикальні функції, за двох аргументах − 16 функцій, за трьох − 256 функцій. Надалі кількість функцій швидко зростає.