3.4 Показатели оценки рыночной активности организации

Данный анализ выполняется финансовыми менеджерами компаний, зарегистрированных на фондовых биржах и котирующий там свои ценные бумаги и любыми участниками фондового рынка.

Для этого анализа недостаточно данных бухгалтерской отчетности, необходима и внешняя информация о положении компании на рынках ценных бумаг. Основными показателями, используемыми в расчетах, являются: количество выпущенных акций, рыночная цена обыкновенной акции, размеры выплачиваемых по акциям дивидендов и др.

Рыночная активность зависит от стратегии и тактики в использовании прибыли, наращивании капитала, выпуска дополнительных акций.

Коэффициент котировки акции — это отношении рыночной цены акции к ее учетной (книжной) цене.

Анализ рыночной и инвестиционной активности предполагает также использование специальных аналитических методов, построения факторных моделей.

3.5 Финансовая оценка вероятности банкротства

В соответствии с Методическими положениями по оценке финансового состояния предприятий и установлению неудовлетворительной структуры баланса, утвержденными распоряжением Федерального управления по делам о несостоятельности (банкротстве) 12.08. 94 г. №31-р с изменением от 12.09.94 г., для признания предприятия неплатежеспособным необходимо наличие одного из следующих условий:

- Коэффициент текущей ликвидности имеет значение менее 2 /3.46/;

- Коэффициент обеспеченности собственными средствами имеет значение менее 0,1 /3.44/.

Финансовая оценка вероятности банкротства может быть выполнена также на основе многофакторных моделей, применяемых в зарубежных странах. Модели дополняют комплексный коэффициентный анализ финансового состояния, рассмотренный выше.

Двухфакторная модель использует коэффициент текущей ликвидности (1) и удельный вес заемных средств в пассивах (2).

3.58

Z>0 — вероятность банкротства велика;

Z<0 — вероятность банкротства мала.

Точность прогноза увеличивается, если расчет выполняется по пяти факторам, предложенным Э.Альтманом:

3.59

Х₁ — отношение собственных оборотных активов/рабочего капитала к сумме всех активов предприятия;

Х₂ — рентабельность капитала;

Х₃ — рентабельность активов;

Х₄ — коэффициент соотношения собственного и заемного капитала;

Х₅ — оборачиваемость активов.

Критическое значение индекса рассчитывалось Э Альтманом по данным статистической выборки и составило 2,675. Расчет индекса и его сопоставление с критическим значением позволяет высказать суждение о возможном в обозримом будущем (2-3 года) банкротстве одних предприятий и устойчивом финансовом положении других. Альтман предложил следующую шкалу:

Значение Z	Вероятность банкротства	Вероятность погрешности
До 1,8	Очень высокая	—
1,81 — 2,70	Высокая	«темная зона» (велика вероятность ошибки)
2,71 — 2,99	Возможная
3,00 и выше	Очень низкая	—

МОДУЛЬ 4 ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ

Обзор ключевых категорий и положений

Эффективность любой финансовой операции, предполагающей наращение исходной суммы PV до ожидаемой в будущем к получению суммы FV (РV → FV), может быть охарактеризована ставкой.

Процентная ставка (процент, рост, ставка процента, норма прибыли, доходность) рассчитывается отношением наращения (FV-PV) к исходной (базовой) величине PV.

Учетная ставка (дисконт) рассчитывается отношением наращения (FV-PV) к ожидаемой в будущем к получению, или наращенной, величине FV.

Соотношение между ставками

Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется процессом наращения, искомая величина - наращенной суммой, а используемая в операции ставка - ставкой наращения. В данном случае речь идет о движении денежного потока от настоящего к будущему.

Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования, искомая величина - приведенной суммой, а используемая в операции ставка - ставкой дисконтирования. В данном случае речь идет о движении от будущего к настоящему.

Величина FV показывает как бы будущую стоимость «сегодняшней» величины PV при заданном уровне доходности.

Величина PV показывает как бы текущую, «сегодняшнюю» стоимость будущей величины FV.

Известны две основные схемы начисления процентов. Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Схема сложных процентов предполагает их капитализацию, т.е. база, с которой происходит начисление, постоянно возрастает на величину начисленных ранее процентов. Очевидно, что более частое начисление сложных процентов обеспечивает более быстрый рост наращиваемой суммы.

Схема простых процентов более выгодна при проведении операций краткосрочного характера (п < 1), а схема сложных процентов -проведении операций долгосрочного характера (п > 1), где п — число начислений процентов.

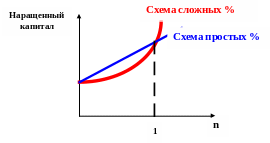
Рис. Простая и сложная схема наращения капитала

Формула простых процентов

Формула сложных процентов

где Р — исходный инвестируемый капитал;

F — размер инвестируемого капитала через n периодов;

r — годовая ставка (требуемая доходность).

FM1(r%,n) — мультиплицирующий множитель для единичного платежа.

Формула дисконтированной (приведенной) стоимости

F_n — денежное поступление в году n;

Р — текущая (приведенная) стоимость, т.е. оценка величины F_n с позиции текущего момента;

r — ставка дисконтирования.

FM2(r%,n) — дисконтирующий множитель для единичного платежа. Он показывает «сегодняшнюю» цену одной денежной единицы будущего, т.е. чему с позиции текущего момента равна одна денежная единица через n периодов от момента расчета, при заданных процентной ставке (доходности) r и частоте начисления процента.

Внутригодовые процентные начисления с целым числом лет

где r — годовая ставка;

m — количество начислений в году;

k — количество лет.

При начислении процентов за дробное число лет более эффективна смешанная схема, предусматривающая начисление сложных процентов за целое число лет и простых процентов за дробную часть года.

Эффективная процентная ставка позволяет сравнивать финансовые операции с различной частотой начисления и неодинаковыми процентными ставками. Именно эта ставка характеризует реальную эффективность операции, однако во многих финансовых контрактах речь чаще всего идет о номинальной ставке, которая в большинстве случаев отличается от эффективной.