Порядок виконання

Порядок виконання завдання 3 розглянемо на прикладі.

1. Зображаємо задану механічну систему і показуємо всі сили, які діють на її елементи(рис. 3.1); - власна вага тіл системи; тертя; - реакції; - рушійна сила, що задається функцією переміщення: F=f(s).

2. Записуємо вираз теореми про зміну кінетичної енергії системи: Так як у початковий момент система була нерухомою, то її кінетична енергія Т₀=0. Отже, рівняння для рішення задачі має вигляд

3. Визначаємо кінетичну енергію системи як суму енергії усіх тіл: . Тіло 1 рухається плоско-паралельно, тому його кінетична енергія

(1)

Тут усі швидкості слід виразити через ту швидкість, яку за завданням слід визначити. Якщо, наприклад, потрібно знайти швидкість центра тяжіння катка 1, тобто то прийнявши до уваги, що точка миттєвий центр швидкостей катка 1, маємо:

(2)

Крім того, моменти інерції катка ; шківа .

Тоді кінетична енергія системи буде дорівнювати(після нескладних перетворень):

(3)

4. Тепер знаходимо суму робіт усіх діючих зовнішніх сил системи на заданому переміщенні катка , виразивши усі переміщення тіл через задану величину . При

Рис. 3.1

цьому слід мати на увазі те, що залежність між переміщеннями буде такою ж, як і між відповідними швидкостями у рівнянні (3), тобто , . В результаті одержуємо:

Робота останніх сил дорівнює нулю, тому що точка , де прикладені і - миттєвий центр швидкостей; точка О, де прикладені сили та , нерухома; реакція , перпендикулярна переміщенню вантажу 3. Тоді

(4)

Порівнюємо вирази (3) та (4)

звідки легко знаходимо .

Зауважимо, що і . Інтеграл функції елементарний інтеграл лінійної функції.

Завдання 4

Для заданого стержня (рис. 4) необхідно:

1. встановити ступінь статичної невизначеності;

2. визначити реакції опор;

3. побудувати епюру поздовжніх сил;

4. побудувати епюру нормальних напружень;

5. перевірити міцність стержня, матеріал якого неоднаково чинить опір розтягу та стиску

Дані взяти з таблиці 4

Таблиця 4. Дані до завдання 4

Параметри	Варіанти
	1	2	3	4	5	6	7	8	9	0
, кН	20	30	40	20	50	30	25	35	45	30
, кН	30	20	20	40	20	50	40	55	25	60
, кН	40	40	30	50	30	20	40	25	35	30
а, м	0,5	0,4	0,6	0,5	0,6	0,5	0,8	0,6	0,4	0,5
b, м	0,7	0,6	0,8	0,4	0,6	0,4	0,6	0,5	0,4	0,5
с, м	0,6	0,5	0,5	0,5	0,4	0,4	0,4	0,8	0,6	0,6
d, м	0,4	0,8	0,7	0,6	0,7	0,6	0,5	0,8	0,6	0,6
А, см2	4,0	4,2	4,4	4,6	4,8	5,0	5,2	5,4	5,5	5,8
МПа	30	35	40	45	50	45	40	50	55	60
МПа	40	50	45	50	60	55	50	60	65	70

Примітки:

1) А - площа поперечного перерізу;

2) - допустиме напруження на розтяг;

3) - допустиме напруження на стиск.

Порядок розрахунку

Розглянемо на конкретному прикладі (рис 4.1,а). Допустимі напруження: =75МПа, =60 МПа. Площа А = 5 см².

1. На заданій розрахунковій схемі конструкції показуємо можливі реакції опор 1 і 2 : R₁ і R₂. Напрям їх довільний (рис 4.1, а).

2. Складаємо рівняння рівноваги: Рівняння одне, а невідомих два - задача один раз статично невизначувана.

3. Вибираємо основну систему (о.с.). Для цього слід відкинути "зайвий" зв'язок, тобто одну з опор. Відкидаємо опору 2 (рис 4.1, б).

4. Навантажуємо систему заданими силами та і реакцією відкинутого зв'язку (опори 2) R₂. Маємо еквівалентну систему (е.с., рис 4.1, в).

5. Складаємо додаткове рівняння деформації стержня, тобто записуємо умову еквівалентності схем а) і в) (рис 4.1): де Застосуємо закон Гука для розтягу і стиску, базуючись на принципі незалежності дії сил:

Рис.4

Рис.4.1

звідки знаходимо

6. Вираховуємо іншу реакцію, тобто реакцію опори 1, використовуючи рівняння рівноваги : . Тут знак "-" вказує на те, що дійсний напрям реакції буде протилежного напряму.

7. Будуємо дійсну еквівалентну систему, враховуючі результат попереднього пункту (рис 4.1, г), тобто показуємо замість опор 1 і 2 дійсні напрями і величини їх реакцій.

8. Будуємо епюру поздовжніх сил. Метод перерізів. Проводимо переріз 1-1 (див рис 4.1, г), і далі розглядаємо ліву частину стержня, (рис 4.1, д). У проведеному перерізі показуємо додатну (тобто направлену від перерізу) поздовжню силу . Складаємо рівняння рівноваги для цієї частини стержня: У будь якому перерізі ділянки а буде Аналогічно визначаємо та . За одержаними даними будуємо епюру поздовжніх сил N (рис 4.1, ж)

9. Будуємо епюру нормальних напружень. Напруження у перерізах ділянки МПа. Аналогічно: МПа; МПа. За отриманими даними будуємо епюр (рис. 4.1, з).

10. Перевірка міцності стержня. Найбільші напруження на розтяг не повинні перевищувати допустимі, тобто У нашому випадку Те ж саме і по відношенню до напружень стиску:

Висновок: стержень задовольняє умовам міцності на розтяг та стиск.

Завдання 5

Для заданої балки на двох опорах (рис. 5) потрібно :

1) визначити реакції опор;

2. побудувати епюри поперечних сил та згинаючих моментів;

3. визначити небезпечний переріз, визначити потрібну величину осьового моменту опору, підібрати балку таких поперечних перерізів: двотавра, круга, квадрата, прямокутника при відношенні висоти до ширини кільця при відношенні внутрішнього діаметра (d) до зовнішнього розташувати визначені перерізи в порядку їх раціональності застосування.

Допустиме напруження прийняти рівним МПа. Дані взяти з таблиці 5.

Таблиця 5. Дані до завдання 5.

Параметри		Варіанти
	1		2	3	4	5	6	7	8	8	0
	40		38	35	32	30	28	25	24	22	20
	28		26	24	22	26	22	20	28	30	35
	16		14	12	16	20	18	16	15	18	22
	1,0		1,2	1,4	1,0	1,2	1,4	1,0	1,2	1,4	1,0
	2,2		2,0	2,4	2,4	2,6	2,4	2,5	2,6	2,4	2,8
	1,8		2,2	2,0	2,2	1,8	2,2	2,0	2,4	2,2	2,6

Рис.5

Порядок виконання

Розглянемо на прикладі (рис 5.1, а).

1. Визначимо опорні реакції. Вертикальні реакції на опорах направимо угору, горизонтальна реакція на лівій опорі явно дорівнює нулю Реакції та рекомендується визначати так одержимо . одержимо . Перевірка:

2. Будуємо епюри поперечних сил і згинальних моментів. На ділянці а балку перетинаємо на дві частини (рис. 5.1, а). Розглядаємо ліву частину, довжиною z_a (рис.5.1, б). Для неї записуємо вирази для поперечної сили та згинального моменту у будь якому перерізі ділянки а : де Надаємо значень , вираховуємо величину Q(z_a) і , будуємо епюри Q і М на ділянці а (рис 5.1, д, е). Слід мати на увазі, що .

3. На рис 5.1, д ми бачимо, що у певній точці тобто на епюрі повинен бути екстремум. Значення знайдемо так: звідки Потім це значення у і знайдемо величину максимуму епюри на ділянці . Для перерізу 2 (рис 5.1, в) . Провівши переріз 3 через ділянку с, розглянемо праву частину балки довжиною (так простіше, ніж брати ліву частину, тобто майже всю балку). Для неї: . Побудувати епюри Q і М для всієї балки показані на рис 5.1, д, е.

4. Підбір перерізів. Умова міцності: . Потрібна величина осьового моменту опору небезпечного перерізу, де діє максимальний згинальний момент (рис 5.1, е), .

   1. Приймаємо двотавр № 16 з W_x=109 см³ та площею перерізу А_дв=20,2 см²

   2. Круглий суцільний переріз:

площа

3.3. Квадратний переріз:

площа

Рис. 5.1

3.4. Прямокутний переріз:

Площа

3.5. Круглий кільцевий переріз, якщо :

площа

4. Визначення раціонального перерізу. Так як вага 1 метру балки пропорційна площі поперечного перерізу, то найбільш раціональним перерізом буде той переріз, який має найменше значення за умов даної задачі. Отже, на першому місці слід поставити двотавр (А_дв=20,2 см²), потім кільцевий переріз (А_кіл=54,8см²) і т.д.

Завдання 6

Стальний вал трансмісії (рис. 6) робить n обертів за хвилину і передає потужність Р(кВт). Потрібно розрахувати вал на згин з крученням, визначити діаметр вала при допустимому напруженні МПа.

Дані взяти з таблиці 6

Таблиця 5. Дані до завдання 5.

Параметри	Варіанти
	1	2	3	4	5	6	7	8	9	0
	5	6	7	8	9	10	11	12	15	18
	100	120	150	180	200	240	260	300	320	350
	1,4	0,8	1,1	1,0	0,9	0,8	0,6	0,7	0,6	0,5
	1,0	1,1	1,2	1,1	0,8	0,8	0,7	0,8	0,5	0,7
	0,8	1,0	0,7	0,6	0,6	0,6	0,6	0,9	0,6	0,7
	150	180	200	220	250	300	320	350	400	420
	200	220	250	260	300	350	380	400	480	520
	30	45	60	45	20	45	30	60	30	75
	60	60	30	30	60	20	40	45	20	40

Порядок розрахунку

Нехай для заданого на рис 6.1, а вала маємо: ; ;

1. Визначається зовнішній скручуючий вал момент

2. Будується епюра крутних моментів: у всіх перерізах вала, розташованих між шківами (рис 6.1, б)

Рис.6

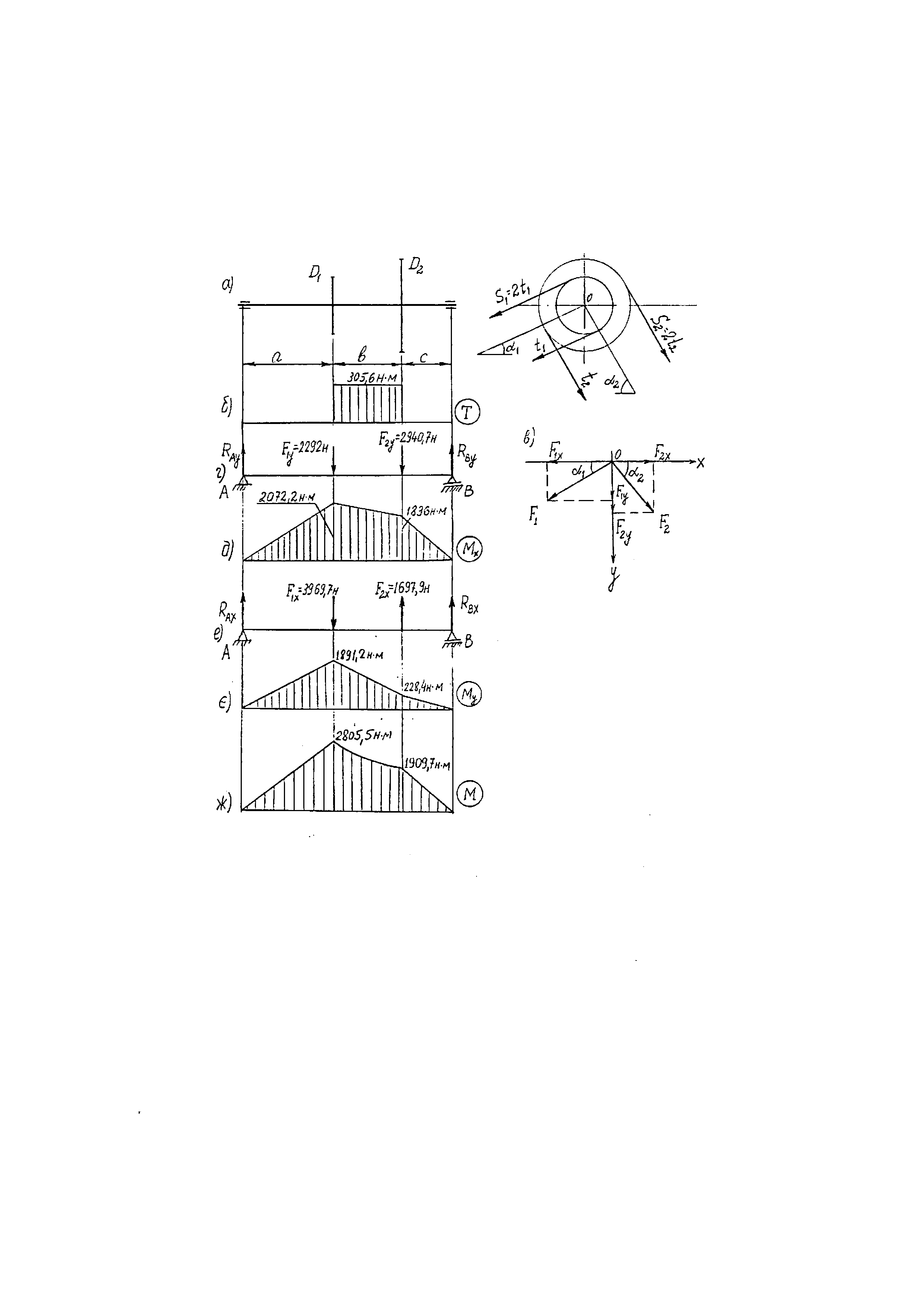
Рис 6.1

3. Визначаються сили натягування гілок пасів (рис 6. схеми 1...6), або сила в зачепленні зубчастих коліс (рис.6 схеми 7...0):

У нашому випадку

4. Визначаються сили тиску на вал з боку шківів:

5. Будується діаграма сил (рис 6.1, в). Визначаються сили, які згинають вал у вертикальній та горизонтальній площинах. У нашому прикладі маємо:

6. Розпікається дія сил на вал у вертикальній площині (рис 6.1, г), будується епюра згинальних моментів відносно осі х-М_х (рис 6.1, д)

7. Розглядається дія сил на вал у горизонтальній площині (рис 6.1, е), будується епюра згинальних моментів М_у (рис 6.1, є)

8. Будується сумарна епюра згинальних моментів за формулою

(рис 6.1, ж)

9. Встановлюється небезпечний переріз. Очевидно, що при наявності сталого крутного моменту небезпечним буде той переріз, де буде мати місце максимальний згинальний момент. У нашому випадку це буде переріз де встановлений шків

10. Використовуючи III або IV теорії міцності для небезпечного перерізу вираховуємо приведений момент: , або

11. Із умови міцності визначаємо діаметр вала де

, або . По ГОСТ 6636-69 визначаємо стандартне зна­чення діаметра вала.

Завдання 7

Виконати структурний та кінематичний аналіз механізму

Схема береться за останньою цифрою шифру з рис.7, а дані до неї з табл.7

Таблиця 7. Дані до завдання 7.

Параметри	Варіант
	1	2	3	4	5	6	7	8	9	0
	0,02	0,025	0,03	0,03	0,035	0,04	0,04	0,03	0,045	0,045
	0,065	0,13	0,16	0,15	0,2	0,21	0,18	0,18	0,15	0,155
	0,08	0,09	0,1	0,08	0,1	0,11	0,1	0,12	0,12	0,09
	0,006	0,01	0,02	0,015	0,03	0,02	0,015	0,02	0,02	0,025
	0,01	0,014	0,015	0,016	0,02	0,015	0,018	0,02	0,017	0,02
	0,06	0,12	0,13	0,12	0,2	0,2	0,17	0,17	0,15	0,14
	300	280	260	240	220	200	180	160	140	120
	30	45	60	75	330	120	150	300	210	240

Порядок виконання завдання