9

9. Трение в машинах

Трение представляет собой явление сопротивления относительному перемещению между двумя телами в зонах соприкосновения поверхностей по касательным к ним. Различают трение скольжения и качения.

9.1. Трение скольжения

Трение скольжение имеет место при относительном движении дух тел, скорости которых в точках касания различны.

Сила трения – это сила сопротивления относительному перемещению двух тел при трении. Она направлена в сторону противоположную возможному направлению относительной скорости V (рис. 9.1). Сила трения определяется по закону Амонтона-Кулона

, (9.1)

где f – коэффициент трения, определяется опытным путем, представляет собой безразмерную величину, например для пар трения: сталь-сталь f =0,15, сталь- чугун f =0,18, сталь-бронза f =0,10;

F_N – сила нормальной реакции опоры (направлена нормально к опираемой поверхности).

При движении тела (рис. 9.1) под воздействием силы нормального реакции F_N появляется сила трения F_Т, равнодействующей этих сил является сила F_R. Угол между равнодействующей F_R сил при трении и силой нормального давления F_N называется углом трения (рис.9.1), обозначается ,

, (9.2)

(9.3)

9.1.1. Трение в поступательной паре (рис.9.1)

Сила трения ползуна о неподвижную опору равна

,

где – сила давления, Н.

Следует указать, что силу реакции опоры вызывает сила давления . По условию равновесия тела (рис. 9.1) (здесь указаны абсолютные величины).

9.1.3. Трение в клиновой паре (рис.9.2)

В клиновой паре наблюдается две плоскости трения по контактирующим боковым поверхностям. Результирующая сила трения в клиновой паре будет равна

,

где силы трения на каждой боковой поверхности, по формуле (9.1) они определяются так

, (9.4)

(9.5).

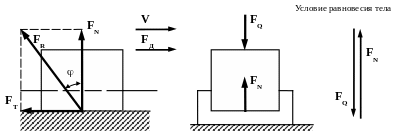
Рис. 9.1. Трение в плоской кинематической паре

Для того, чтобы определить силы нормальной реакции опоры (они перпендикулярны поверхностям трения) рассмотрим равновесие ползуна под действием силы давления , которая вызвала силы реакции опоры и . условие равновесия клинового ползуна – векторный треугольник должен быть замкнут. Из этого треугольника (рис.9.2) определяем силу нормального давления и . Тогда уравнения (9.4) и (9.5) запишутся в виде.

, ,

где 2 – угол вершины клина.

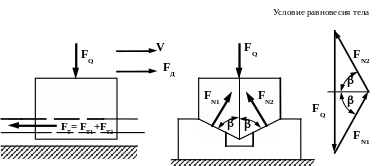
Рис. 9.2. Трение в клиновой кинематической паре

В итоге сила трения в клиновой паре равна

(9.6).

Величина называется приведенным коэффициентом трения

. (9.7).

Анализ формулы (9.6) показывает: сила трения в клиновой паре может быть гораздо больше силы трения в поступательной паре при одинаковых и , что достигается за счет угла клина 2. При малых углах 2 и приведенный коэффициент трения и сила трения могут достигать достаточно больших значений, это используется для получения больших сил трения, например, в сверлах с конусами Морзе, в конических соединениях валов, ременных передачах с клиновым ремнем, крепежных резьбах и др.