МИНИСТЕРСТВО ОБРАЗОВАНИЯ ТВЕРСКОЙ ОБЛАСТИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ « ТВЕРСКОЙ КОЛЛЕДЖ ИМЕНИ А.Н.КОНЯЕВА» Курсовой проект По предмету «Автоматическое управление» Тема курсового проекта «Решение уравнений систем автоматического регулирования» специальность 220703 Работу выполнил студент группы 4П2 Борисов Андрей Борисович Тверь 2014

Содержание

Практическая работа №1

Практическая работа №2

Практическая работа №3

Практическая работа №6

Практическая работа №8

Практическая работа №9

Практическая работа №1 «Операторный метод решения дифференциальных уравнений»

1. Цель работы исследовать возможности операторного метода решения дифференциальных уравнений, описывающих работу системы.

2. Пояснение к работе.

2.1 Краткие теоритические сведения

Операторная форма записи дифференциальных уравнений – это такая их своеобразная форма запаси, когда операции дифференцирования и интегрирования заменяют алгебраическими операциями над числом P.

При решении дифференциальных уравнений операторным методом переходят от данных функций, называемых оригиналами x(t), к их изображениям x(p); совершают более простые действия над полученными изображениями, а затем полученный результат в виде изображения переводят в оригинал, т.е. по найденному изображению находят оригинал. Преобразование Лапласа – интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчетах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свертка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Идея операционного исчисления состоит в следующим. Пространство функций, удовлетворяющих некоторым достаточно общим условиям (пространство функций-оригиналов) взаимно однозначно отражается в другое пространство функции (пространство функции-изображения) так, что операциям дифференцирования и интегрирования в пространстве функции-оригиналов соответствуют более простые операции (конкретно операции умножения и деления) в пространстве функции-изображений. В результате дифференциальное уравнение в пространстве функций-оригиналов преобразуется в линейное алгебраическое уравнение в пространстве

функций- изображений, решение которого находится без проблем. Последнее действие – восстановление решений уравнения по его изображению.

3. Задание:

Используя операторный метод решить дифференциальное уравнение , описывающее RL цепь относительно тока i(t), т.е. найти i(t).

Исходные данные:

Дифференциальное уравнение i*R+L*di/dt=U_вх

U_вх=380В; R=200Ом; L=200Гн

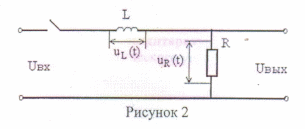
Решение:

U_R(t)+u_L(t)=U_вх

I*R(t)+u_L(t)=U_вх

I(t)=L*du_L(t)/dt

R*L*du_L(t)/dt+u_L(t)=U_вх

Заменим d/dt на p получим изображение:

R*L*p U_L(p)+U_L(p)=U_вх

Вынесем U_L(p) за скобки:

U_L(p)*(R*L*p+l)=U_вх

Найдем U_L(p):

U_L(p)=U_вх/(R*L*p+l)

Чтобы воспользоваться таблицей и перейти от изображения к оригиналу необходимо свести данное выражение к табличному, для этого поделим числитель и знаменатель на RL и получим:

Ul(p)=U_вх/R*L/(p+l/R*L)

l/RL есть а, тогда

l/p+a=l/p+a/RL

Изображение U_вх/RL соответствует оригиналу U_вх/RL, а изображение l/p+l/RL – оригиналу l-e^-t/RL, т.е. получаем

Ul(t)=U_вх/RL*(1-e^-l/RL*t)

Ul(t)=9.7В