5. Конструктивный расчет антенны

5.1 Расчёт профиля зеркала

Зеркальные антенны имеют наибольший КНД при синфазном возбуждении раскрыва. Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва. В полярной системе координат парабола описывается уравнением:

(5.1)

где ,  - полярные координаты, f₀ - фокусное расстояние. В данном случае  изменяется от 0 до ₀, т.е. от 0^o до 47^o.(приложение А, рисунок 5.1).

5.2 Выбор конструкции зеркала

С целью уменьшения веса и ветровых нагрузок поверхность зеркала часто выполняется перфорированной или сетчатой (рисунок 5.1).

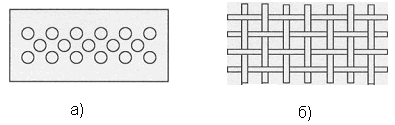
Рисунок 5.2 - Перфорированная (а) и сетчатая (б) поверхность зеркала

При такой конструкции зеркала часть энергии просачивается сквозь него, образуя нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении:

(5.2)

где Р_обр, Р_пад - мощность излучения в обратном направлении и падающего на зеркало, соответственно. Двух линейная сетка работает удовлетворительно при расстоянии между проводниками l < 0.1 = 16.7мм и диаметре проводов d  0.01 = 1.67мм.

5.3 Определение допусков на точность изготовления

Неточность изготовления зеркала вызывает несинфазность поля в раскрыве. Допустимыми являются фазовые искажения поля в раскрыве зеркала не более ± /4. При этом уменьшение коэффициента усиления антенны не превышает нескольких процентов [3].

Пусть поверхность параболоида имеет некоторые неровности с наибольшим отклонением от нормы  (рисунок 5.3).

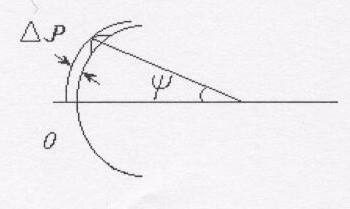
Рисунок 5.3 - Допуски на точность изготовления зеркала

Путь луча, отраженного от поверхности в месте наибольшего отклонения от  изменяется при этом на величину

 +   cos(), (5.3)

а соответствующий сдвиг фаз составит величину и он не должен превышать /4, отсюда получаем:

(5.4)

Анализ полученного выражения показывает, что в близи центра параболоида необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превышать

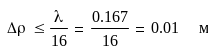
у кромки параболоида требования к точности получаются наименьшими. Точность установки облучателя так же определяется нормами на наибольшие допустимые фазовые искажения поля в раскрыве [6].

Пусть фазовый центр облучателя смещён на x (рисунок 5.3).

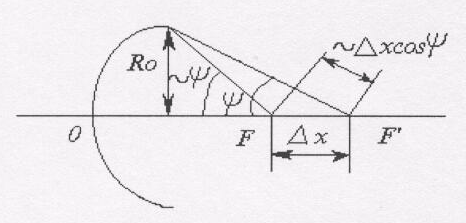
Рисунок 5.4 - Допуски на точность установки облучателя

Тогда длины путей лучей от фазового центра до раскрыва увеличиваются. Наибольшее удлинение пути происходит у лучей, падающих на вершину зеркала. Это удлинение путей при малых смещениях можно приблизительно определить как xcos(). Тогда изменение фазы составит величину:

(5.6)

где ₀, _a- фазовые искажения, возникающие из-за неточности установки облучателя, в центре и на краю раскрыва, соответственно. Эта величина не должна превышать /4, отсюда получим, что

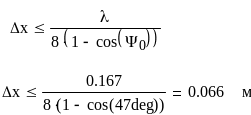(5.7)

Таким образом, с увеличением угла раскрыва точность и установка облучателя в фокусе повышается.

Выводы:

Подводя итог проделанной работы, можно выделить следующие моменты:

1. с увеличением угла раскрыва точность и установка облучателя в фокусе повышается;

2. ширина ДН на уровне повинной мощности:

• 2_0.5 =76 мрад (по условию)

• 2_0.5 =74 мрад (по расчетам), что вполне допустимо, т.к. это составляет около 2.6 % (допустимое значение до 5%);

3. УБЛ:

• -24 дБ (по условию)

• -23.071 дБ, что несколько больше допустимого. Для уменьшения уровня боковых лепестков можно рекомендовать увеличить радиус раскрыва антенны.