Тема 2. Графічний метод розв’язування задач лінійного програмування на координатній площині

1. Графічне зображення лінійних обмежень-рівнянь і нерівностей.

2. Знаходження області допустимих значень для основної задачі лінійного програмування-2 з однією і двома невідомими.

3. Визначення ліній min і max рівня.

Для кращого розуміння алгебраїчних властивостей задач лінійного програмування скористаємось їх геометричною інтерпритацією. Введемо поняття опуклої множини.

Означення 1. Множина точок М називається опуклою, якщо разом з будь – яким двома її точками множині належить і відрізок, що їх сполучає.

Означення 2. Множина називається обмеженою, якщо її можна помістити в кулю (коло) скінченого радіуса з центром в будь – якій точці множини, і необмеженою в протилежному випадку.

Означення 3. Граничною називається така точка множини, в довільному околі якої є і точки, що належать множин, і точки, що їй не належать.

Означення 4. Сукупність граничних точок множини називається її границею.

Найпростіший приклад опуклої множини – опуклий многокутник. Його границя складається з відрізків чи прямих. Точки, в яких перетинаються відрізки чи прямі границі многокутника називаються його вершинами.

Означення 5. Перетином областей називають множину точок, що належать кожній з цих областей.

Теорема 2. Перетин будь – якого числа опуклих областей завжди є опукла множина.

Для геометричної інтерпритації будемо розглядати ОЗЛП з ОН, які містять лише дві невідомі, оскільки вони легко відображаються на прямокутній декартовій системі координат. Задачі з трьома невідомими на малюнку розглядатимуться в проекції, що утруднить їх розгляд, а задачі з більшою кількістю невідомих взагалі важко уявити геометрично.

Розглянемо задачу лінійного програмування:

(5)

(6)

Лема 3. Розв’язком нерівності є півплощина.

Означення 6. Півплощину, побудовану за нерівністю називають півплощиною розв’язків нерівності, її границю – граничною прямою .

Означення 7. Сукупність точок, яка задовольняє систему нерівностей (5), називають многокутником розв’язків (або областю допустимих значень-ОДЗ).

Теорема 3. Многокутник розв’язків завжди є опуклою фігурою.

Теорема 4. Оптимальне значення задачі лінійного програмування досягається у вершині многокутника розв’язків.

Таким чином задачу лінійного програмування можна інтерпретувати так: у многокутнику розв’язків знайти таку вершину, де цільова функція набуває найменшого (найбільшого) значення.

На основі геометричної інтерпретації сформуємо алгоритм графічного методу відшукання оптимальних значень функції.

1. Будуємо многокутник розв’язків. Він складається з перетину окремих півплощин розв’язків системи (5). В силу обмежень многокутник розв’язків завжди міститься в першому квадранті.

2. Знаходимо оптимальну точку. Вона міститься в вершині многокутника розв’язків. Для її відшукання відкладають вектор нормалі прямої , . Потім рисуємо лінію перпендикулярну до вектора нормалі, вона називається лінією рівня. Пересуваючи лінію рівня в напрямі вектора нормалі до останньої вершини многокутника розв’язків, отримуємо точку максимуму цільової функції, пересуваючи цю лінію в протилежному до вектора нормалі напрямі, в останній вершині дотику отримуємо точку мінімуму цільової функції.

3. Обчислюємо оптимальні значення. Знаходимо координати вершин max і min, як розв’язок системи рівнянь, що визначають сторони многокутника, що утворюють ці вершини. Знайдені координати підставляємо в форму (6).

Зауважимо, що якщо многокутник розв’язків необмежений, то можливо, що мінімального чи максимального (або й обох) значень не існує, тобто – це +∞ чи –∞.

Приклад.

Знайти найбільше та найменше значення функції , за умов обмеження

Розв’язування. Побудуємо прямі, що відповідають рівнянням, зрозумілим з системи обмежень та відмітимо ті півплощини, що відповідають нерівностям обмежень.

, пряма проходить через точки (1; 3) і (10; 0);

, пряма проходить через точки (0; 6) і (6; 0);

, пряма проходить через точки (0; 5) і (2; 1).

Умова вказує на достатність розгляду в першому квадранті.

Всім умовам належності до відповідних півплощин відповідає чотирикутник ABCD. Будуємо вектор нормалі до цільової функції і переміщаємо пряму перпендикулярно до цього вектора. Перший раз ця пряма перетинає трикутник в вершині D(2,5; 0), отже . Остання вершина дотикається до прямої вздовж її руху – це точка С(6; 0), звідси .

Завдання 2

Графічним методом знайти розв’язок задачі лінійного програмування (х₁0, х₂0):

1. z=–7х₁–6х₂+19 (min) 2. z=9х₁+3х₂+8 (max)

3. z=–4х₁+7х₂ (min) 4. z=8х₁+7х₂ (max)

5. z=2х₁+3х₂ (min) 6. z=3х₁+2х₂ (max)

7. z=х₁+2х₂ (max) 8. z=6х₁+5х₂–30(min)

9. z=8х₁+4х₂+22(max) 10. z=4х₁+х₂ (max)

11. z=–7х₁–6х₂+19 (min) 12. z=–9х₁+3х₂+8 (max)

13. z=4х₁+7х₂ (max) 14. z=8х₁+7х₂ (max)

15. z=–3х₁–2х₂ (min) 16. z=х₁+2х₂ (max)

17. z=2х₁+3х₂ (max) 18. z=–8х₁–4х₂+22(min)

19. z=–4х₁+х₂ (max) 20. z=–3х₁–2х₂+10(min)

21. z=6х₁+6х₂+10(max) 22. z=–5х₁–3х₂+5(min)

23. z=5х₁–6х₂+12(max) 24. z=–5х₁–4х₂+11(min)

25. z=3х₁+4х₂ (max) 26 z=5х₁+2х₂+4(min)

27 z=х₁+3х₂+6(max) 28 z=–3х₁–2 х₂ (max)

29. z=2х₁+4 х₂–3(max) 30. z=–3х₁–х₂+4(min)

31. z=2х₁+2х₂+6(max) 32. z=6–2х₁–3х₂ (min)

33. z=–9х₁–3х₂+8 (min). 34. z=14х₁+7х₂ (max).

35 z=х₁+3х₂+6(min) 36 z=–3х₁–2 х₂ (max)

37. z=2х₁+4 х₂–3(max) 38. z=–3х₁–х₂+4(min)

39. z=2х₁+2х₂+6(min) 40. z=6–2х₁–3х₂ (min)

41. z=9х₁+3х₂+8 (max). 42. z=14х₁+17х₂ (max).

43 z=2х₁+3х₂+6(max) 44 z=–13х₁–12 х₂ (max)

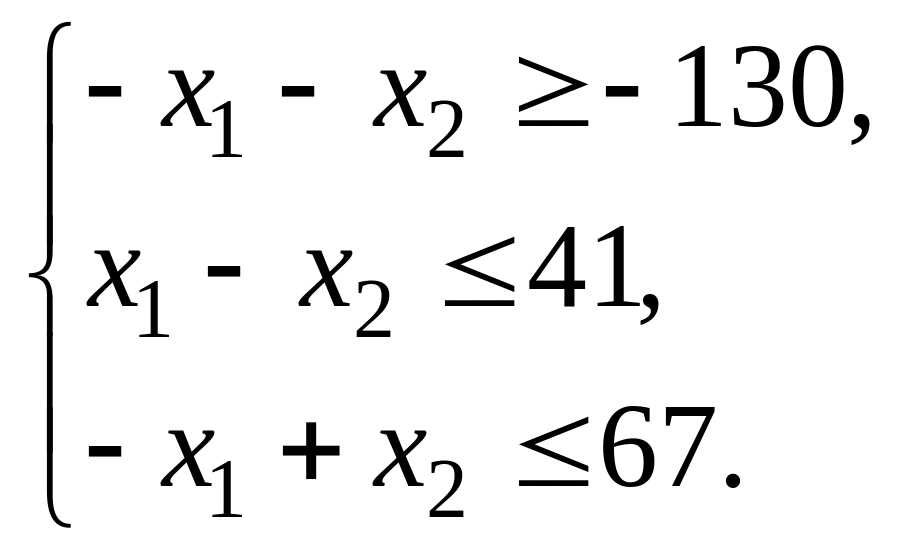
45. z=12х₁+4 х₂–3(max) 46. z=–3х₁–2х₂+4(min)

47. z=7х₁+2х₂+6(max) 48. z=6–2х₁–3х₂ (min)

49. z=9х₁+13х₂+8 (max). 50. z=14х₁+17х₂ (max).

Завдання 3

Графічно знайти оптимальний план задачі завдання 1.

Контрольні запитання для самоконтролю.

1. Які є типи задач лінійного програмування?

2. Сформулюйте задачі лінійного програмування з обмеженнями – рівностями та обмеженнями – нерівностями.

3. Які твердження визначають взаємозв’язок між ОЗЛП з ОР та ОЗЛП з ОН?

4. Яка множина називається опуклою?

5. Яка множина називається обмеженою, необмеженою?

6. Що таке гранична точка? Границя?

7. Сформулюйте теорему про перетин довільного числа опуклих областей.

8. Що таке півплощина розв’язків, гранична пряма, многокутник розв’язків?

9. Де знаходиться оптимальне значення ЗЛП?

10. Сформулюйте алгоритм графічного методу.

11. Що таке вектор нормалі, лінія рівня?

12. Як обчислити оптимальні значення цільової функції?