Основная задача линейного программирования.

В общем виде задача линейного программирования (ЗЛП) ставится следующим образом.

Найти вектор х=(х₁,х₂, ... x_n) в Rⁿ, который максимизирует (или минимизирует) целевую функцию

F(x)=с₁х₁+с₂x₂ +... +с_nx_n (3)

и удовлетворяет m+n линейным неравенствам:

a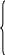 ₁₁х₁+a₁₂x₂+...+a_1nx_n ≤ b₁

a₂₁x₁+a₂₂x₂+...+a_2nx_n ≤ b₂

. . . . . . . . . . . . (4)

a_m1x₁+a_m2x₂+...+a_mnx_n ≤ b_m

x₁0, x₂0, ... x_n0

В терминологии программирования линейная функция F(х) называется целевой функцией задачи. Множество решений системы линейных неравенств (4) называют множеством допустимых решений, а любой вектор х из этого множества называется допустимым решением. Оптимальным решением называется вектор х*, при котором целевая функция принимает своё максимальное (или минимальное) значение на допустимом множестве решений.

Графический метод решения задач линейного программирования. Покажем, как решается указанная задача графическим (геометрическим) методом. Для этого ограничимся рассмотрением системы линейных неравенств с двумя неизвестными.

Пусть задана целевая функция F=с₁х₁+с₂х₂+с₀. Найдём среди множества точек (х₁,х₂) из области допустимых решений совместной системы неравенств (4) (содержащей только переменные x₁ и x₂) такие, которые придают линейной функции F наименьшее (наибольшее) значения. Для каждой i – ой точки плоскости функция F принимает фиксированное значение F=F_i. Множество всех таких точек на которых функция F принимает одно и то же значение F_i есть прямая с₁х₁+c₂х₂+c₀=F_i = const, перпендикулярная к некоторому вектору, называемому градиентом F (grad F). Этот вектор выходит из начала координат и имеет координаты grad F =(с₁,с₂). По свойству вектора grad F если указанную прямую передвигать параллельно самой себе в положительном направлении вектора grad F, то значение целевой функции F=с₁х₁+с₂х₂+с₀ на этой прямой будет возрастать, а в противоположном направлении - убывать.

Пусть при движении прямой F=const в положительном направлении вектора grad F эта прямая впервые встретится с многоугольником допустимых решений в его вершине. Тогда в этом положении F₁ прямая F=const называется опорной, и на этой прямой функция F принимает наименьшее значение. При дальнейшем движении в том же направлении (положительном) прямая F=const пройдёт через другую вершину многоугольника допустимых решений и выходя из области решений также станет опорной прямой F₂. На ней функция F принимает наибольшее значение среди всех значений, принимаемых на многоугольнике допустимых решений. Таким образом, минимизация и максимизация целевой функции F=с₁х₁+с₂х₂+с₀ на многоугольнике допустимых решений достигается в точках пересечения этого многоугольника с опорными прямыми F=с₁х₁+с₂х₂+с₀ = const, нормальными к вектору grad F=(с₁, с₂). Это пересечение опорной прямой с множеством допустимых решений может быть либо в одной точке (вершине многоугольника), либо в бесконечном множестве точек (если это множество сторона многоугольника).

Задание по первой, второй, третьей задаче выбирается по фамилии имени отчеству студента, а по четвертой задаче выбирается по фамилии и отчеству.

Задача №1

Таблица 1

Первая буква	Фамилия									Имя			Отчество
	a11	a12	a21	a22	a31	a32	a41	a42	b1		b2	b3	C0	C1	C2
А	4	6	2	10	3	5	4	12	400		500	600	5	5	7
Б	6	4	8	3	5	4	2	16	500		400	700	8	9	10
В	4	8	4	5	4	2	7	12	600		700	400	11	12	13
Г	8	10	6	14	2	9	2	13	700		800	300	13	5	6
Д	10	5	4	16	4	2	3	4	800		300	250	7	8	9
Е	5	4	2	1	6	4	4	13	300		250	260	10	11	12
Ж	4	2	1	2	3	6	4	6	250		260	400	4	6	5
З	2	1	2	3	4	3	6	14	260		400	250	8	7	9
И	1	2	3	4	3	6	9	16	400		260	270	11	10	12
К	2	3	2	13	6	7	8	9	280		400	320	4	11	5
Л	3	1	3	2	9	8	5	6	270		320	400	6	7	8
М	1	3	6	4	2	5	6	7	250		450	310	9	10	11
Н	3	6	3	8	1	2	4	16	450		310	410	12	4	5
О	6	3	8	3	6	7	6	5	310		410	315	6	7	9
П	7	8	3	6	3	6	1	2	415		315	400	10	12	4
Р	8	1	6	3	6	3	4	5	230		400	281	6	8	7
С	4	6	5	6	3	7	3	1	400		282	150	8	10	9
Т	6	7	6	5	4	3	2	13	283		400	231	11	12	10
У	2	6	1	4	5	7	3	9	150		284	400	6	9	7
Ф	6	4	5	2	7	6	8	13	290		150	285	7	9	8
Х	1	6	7	5	6	2	4	5	300		290	150	5	7	6
Ц	2		6	6	5	4	5	3	360		300	287	8	5	6
Ч	3	2	6	6	4	5	3	5	270		288	400	4	10	5
ШЭ	4	6	5	4	6	3	5	11	289		400	291	5	6	7
ЮЯ	5	9	4	7	3	6	2	5	200		290	308	6	7	4

Пример 4: Минимизировать линейную форму F=14x₁+4x₂ при ограничениях:

7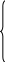 х₁+ 2х₂  14

-х₁ + х₂ 2

4 х₁ –7x₂ ≤ 14

8x₁+ 9x₂ 72

x₁ 0, x₂ 0.

Решение.

Заменив знаки неравенств на знаки точных равенств, получим уравнения границ области допустимых решений. По уравнениям, полученных прямых построим искомую область:

7х₁+2х₂ =14

-х₁+х₂ =2

4 х₁ – 7x₂ = 14

8x₁+9x₂=72

x₁=0, x₂ =0.

Областью допустимых решений системы неравенств является многоугольник ABCDE.

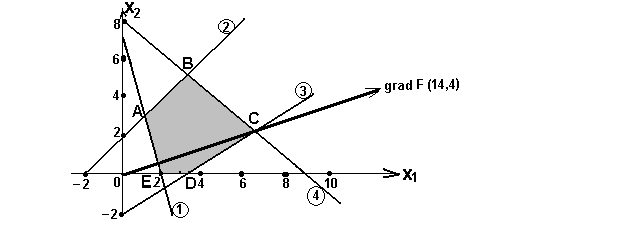рис 5.

Для нахождения точек экстремума построим прямую F=14x₁+4x₂=0 и вектор gradF = (14, 4). Будем передвигать прямую F=0 параллельно самой себе в направлении вектора grad F. С многоугольником ABCDE эта прямая впервые встретиться в точках Е(2,0) и А(10/9, 28/9), где целевая функция принимает одно и то же минимальное значение F(E) = F(A) =14·2+4∙0=28-min, (т.к. вектор grad F перпендикулярен прямой АЕ). Таким образом, минимальное значение целевая функция принимает в любой точке отрезка AE.

Из плана основной задачи линейного программирования следует, что число его положительных компонент не превышает .

Опорный план называется невырожденным, если он содержит ровно положительных компонент; в противном случае план является вырожденным.

Любые переменных системы линейных уравнений с переменными (при условии ) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные переменных называются не основными.

Базисным решением системы m линейных уравнений с переменными называется всякое ее решение, в котором все не основные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с угловой точкой множества допустимых решений.

Следствие. Если оптимальное решение не единственное, то таких решений будет множество (например, все точки отрезка, соединяющего соответствующие угловые точки ).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых значений, и наоборот.