Тимакин о.А.

Методы оптимальных решений

Учебное пособие

с вариантами заданий по контрольной работе

для студентов экономических специальностей

2 курса заочного отделения по направлению подготовки «Экономика», профилям «Бухгалтерский учет, анализ и аудит», «Финансы и кредит»

2013

УДК 517 (075.4)

Тимакин О.А. Учебное пособие. Для студентов 2 курса заочного отделения по направлению подготовки «Экономика», профилям «Бухгалтерский учет, анализ и аудит», «Финансы и кредит». Ростов-на-Дону, 2013 г.– 45 с.

В учебном пособии приведены содержание четырех разделов дисциплины «Методы оптимальных решений» в соответствии с Учебной программой дисциплины, основные теоретические положения дисциплины, вопросы к зачету варианты контрольной работы №1 для студентов заочной формы обучения, рассмотрено решение типового варианта контрольной работы, приведены правила оформления контрольной работы и перечень рекомендуемой учебной литературы.

Пособие предназначено для студентов заочной формы обучения и заочной формы на базе высшего и среднего образования.

Рецензент:

Печатается по решению кафедры «Экономическая кибернетика »

© Тимакин О.А.

Методы оптимальных решений

"Методы оптимальных решений" являются разделом (частью) теории исследования операций, основой которой служит математическое моделирование экономических процессов и явлений. Математическое моделирование - это теоретический и экспериментальный метод познавательной деятельности, способ исследования и объяснения явлений, процессов и систем на основе создания новых объектов, называемых математическими моделями. Математические методы исследования используют в экономике, социологии, в коммерческой деятельности и т.д. Коммерческая деятельность связана с постоянным поиском наиболее выгодного варианта распределения различных ресурсов: финансовых, товарных, технических и др. Чтобы сформулировать оптимальный план выпуска продукции, доставки и реализации товаров, необходимо применять специальные методы решения соответствующих задач.

Рассмотрим основные понятия и теоремы математики, с помощью которых решаются названные задачи.

Понятие выпуклого множества. Линейная функция.

Пусть S является подмножеством R² (точек плоскости).

Множество S называется выпуклым множеством, если каждая точка отрезка прямой, соединяющей любые две точки S, так же принадлежит S.

Иначе это можно сформулировать так: множество S в R² называется выпуклым, если для любых двух элементов а и b , таких что a,bS следует,

что (l - t)·a + t·b S при 0 ≤ t ≤ l.

Последнее выражение определяет все внутренние точки отрезка прямой, соединяющего заданные точки а и b.

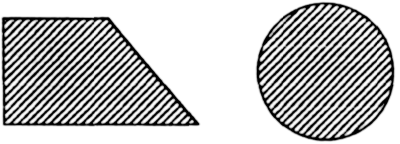
выпуклые множества

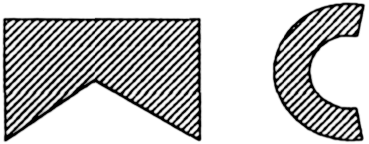
не выпуклые множества

По аналогии в общем случае отрезком в Rⁿ прямой, соединяющим две точки а=(а₁,а₂... a_n) и b=(b₁,b₂ ... b_n) из Rⁿ , называется множество точек, удовлет-воряющих соотношению: (1-t)·a + t·b; 0 ≤ t ≤ l.

Определение: Функция f(x), определённая для х=(х₁,х₂ ... х_n)Rⁿ называется линейной, если f (х) = c₀ + c₁x₁ + c₂x₂ +... + c_nx_n при некоторых постоянных c₀, c₁, c₂,... c_n

Уравнение прямой в пространстве R² можно записать в виде

a₁x₁+a₂x₂ = b (1)

где a_1, a₂ и b - действительные числа; x₁, x₂ – текущие координаты прямой.

Прямая (1) разбивает R² на три непересекающиеся подмножества, S₁,S₂,S₃, то есть R² = S₁+ S₂+S₃, где

S₁ = {(х₁,х₂) : a₁x₁+a₂x₂ = b}

S₂ = {(х₁,х₂) : a₁x₁+a₂x₂ > b}

S₃ = {(х₁,х₂) : a₁x₁+a₂x₂ < b}

При этом точками подмножества S₁ служат точки, лежащие на прямой (1), а подмножеств S₂ и S₃ - внутренние точки полуплоскостей, на которые прямая (1) разбила всю плоскость. Множества S_1, S₂ и S₃ изображены на рис.1.

S₁

рис.1

В общем случае в n-мерном пространстве Rⁿ вводятся определения.

Множество H={х= (х₁,х₂,...х_n): a₁x₁+a₂x₂+...+a_nx_n=b}, где

а₁, а₂ ... a_n и b - действительные числа, называется гиперплоскостью в Rⁿ.

Точка х в Rⁿ называется вершиной многогранного выпуклого множества D, если х D и х является точкой пересечения n граничных гиперплоскостей, которые определяют D. Вершину называют так же угловой (или крайней) точкой многогранного выпуклого множества.