Вірші про теорему Піфагора теорема пифагора

Если дан нам треугольник

И притом с прямим углом,

То квадрат гипотенузы

Мы всегда легко найдём:

Катеты в квадрат возводим,

Сумму степенем находим –

И таким простым путём

К результату мы придём.

Пифагорова теорема

Не знаю, чем кончу поэму,

И как печаль мне избыть,

Древнейшую теорему

Никак я не в силах забыть.

Стоит треугольник, как ментор,

И угол прямой в нём есть.

И всем его элементам

Повсюду покой и честь.

Прелестная гіпотенуза

Взнеслась так смело ввись!

И с нею в Верном союзе

Два катета тоже взнеслись.

Она царит на квадратах,

И песню поёт она.

Та песня влечёт куда-то

Геометров древних волна.

Гимн гипотенузе

Как символ вечного союза,

Как вечный символ, знак простой,

Связала гипотенуза

Навеки катеты собой.

Путей окольных избегая

И древней истине верна,

Ты по характеру – прямая

И по обычаю точна.

Скрывала тайну ты, но скоро

Явился некий мудрый грек

И теоремой Пифагора

Тебя прославил он на век.

Хранит тебя безмолвно, чинно

Углов сторожевой наряд,

И копья – острые вершины

На обе стороны грозят.

И если двоечник, конфузясь,

Немеет пред твоим лицом,

Пронзит его гипотенуза

Своим отточенным копьём.

Сто доведень теореми Піфагора

Ця теорема була відома і в Стародавній Індії. Про це свідчать наступні слова , які містяться у «Сутрах».

1). Квадрат діагоналі прямокутника дорівнює сумі квадратів його більшої і меншої сторін.(рис.10)

2) Квадрат на діагоналі квадрата в два раза більше самого квадрата.(рис.2)

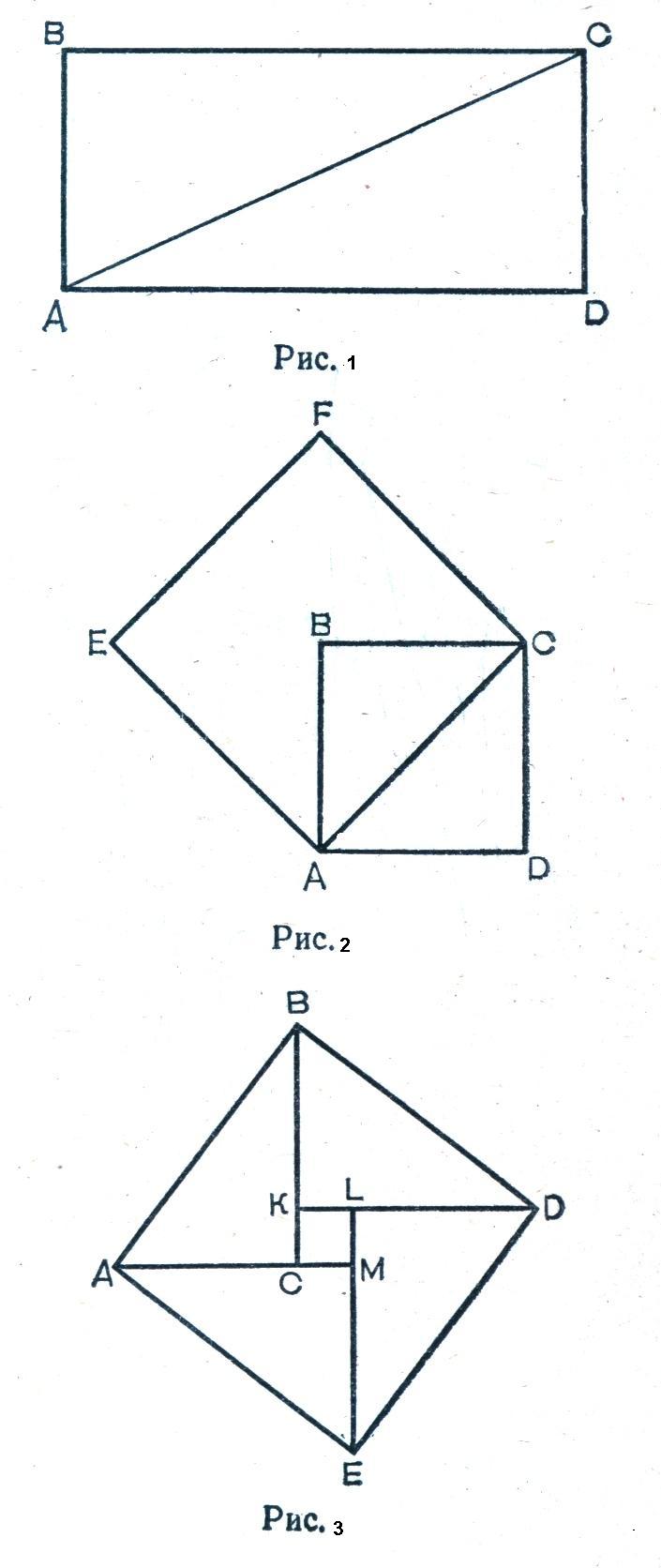
Найстаріше доведення теореми Піфагора знаходиться в одній із праць Бхаскари і полягає у слідуючому (рис.3).

Нехай ABDE – квадрат, сторона якого дорівнює гіпотенузі прямокутного трикутника АВС(АВ=с, ВС=а, АС= b).

Нехай DK , тоді

∆АВС=∆ВDК=∆DEL=∆AME. Тому KL=CM=LM=

=CK=a-b.

Отже,

Ще одне доведення теореми Піфагора викладено Евклідом в «Началах». Як формуліровка, так і доведення мають у Евкліда чисто геометричний характер. На гіпотенузі і катетах прямокутного трикутника ВАС (рис.4) побудовано відповідні квадрати і доводиться, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах.

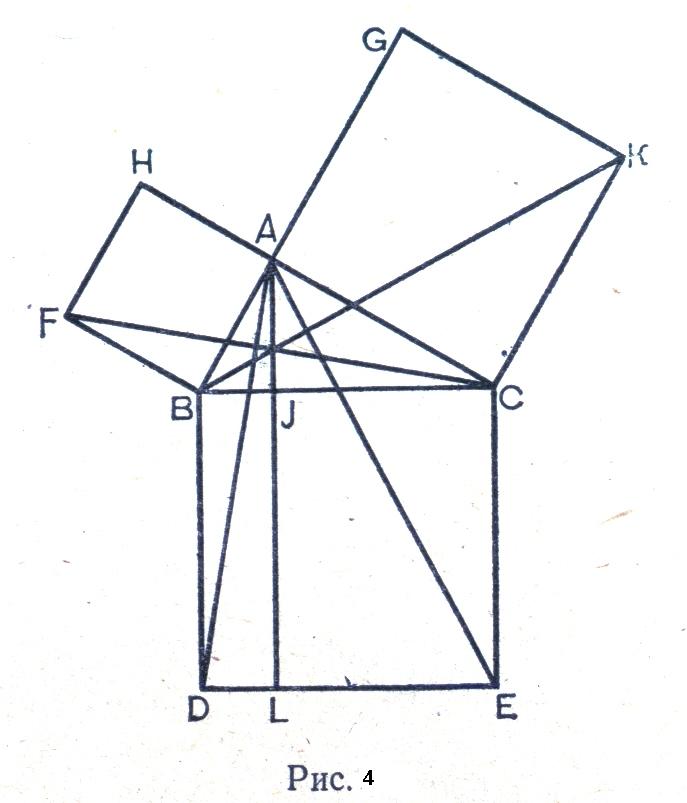
Більшість із даних після Евкліда доведень теореми Піфагора основані на тому, що рівно складені фігури рівновеликі: квадрати. Побудовані на катетах і гіпотенузі, розбиваються на многокутники так, що кожному многокутнику із скаду квадрата на гіпотенузі відповідає рівний многокутник одного із квадратів на катетах. В таких випадках досить подивитися на малюнок. Щоб зрозуміти усе доведення. Багдадський математик та астроном Х ст.Анарицій дав таке доведення – (рис. 5)

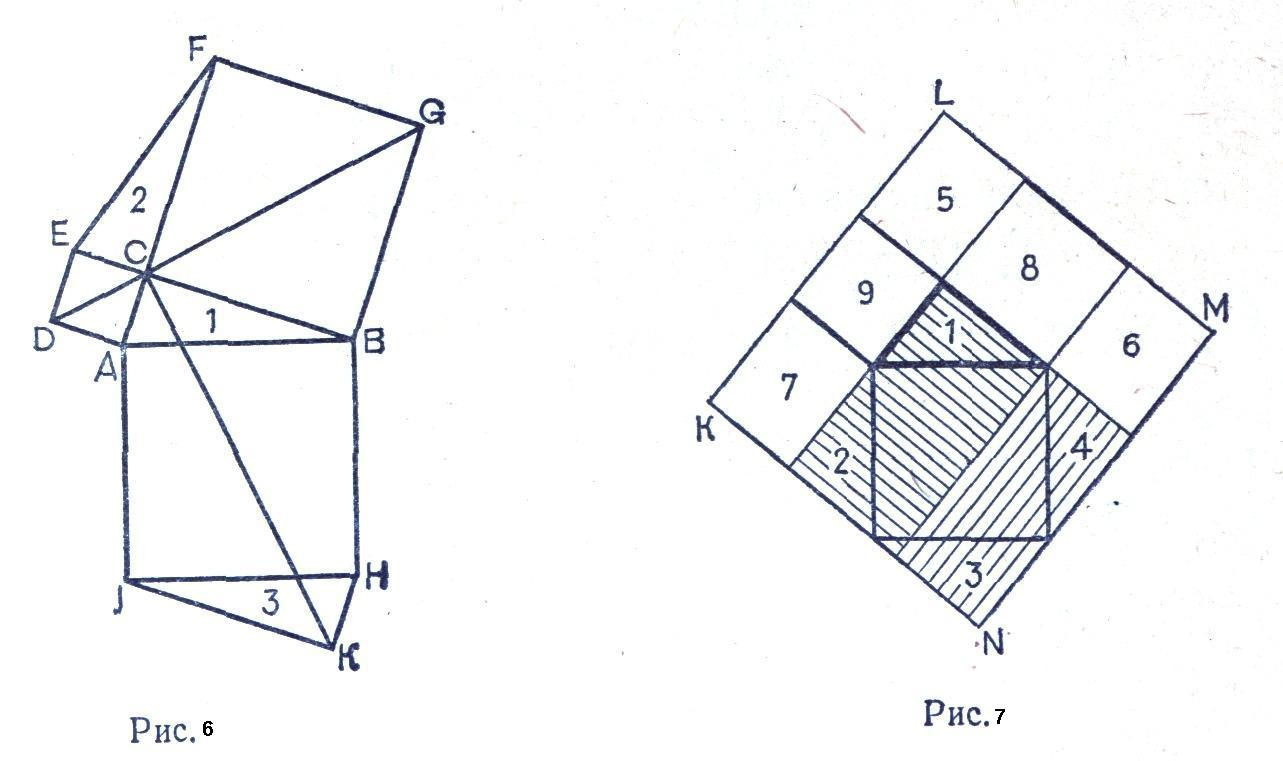
Інші доведення основані на тому,що, додаючи до квадратів на катетах і до квадрату на гіпотенузі рівні фігури, отримуємо рівновеликі фігури. Наприклад на рисунку 6 до Піфагорової фігури добавлені трикутники 2 і3, рівні даному трикутнику 1. Доведення теореми Піфагора зводиться до доведення рівновеликості шестикутників DABGFE і CAJKHB. Останнє видно з того, що пряма DG ділить пополам перший , пряма СК – другий шестикутник. А якщо повернути половину першого шестикутника DABG навколо точки А на 90°, то вона співпаде з САJK, половиною другого шестикутника.

Ще одне доведення (рис. 7). Тут Піфагорові фігура достроєна до прямокутника KLMN. Віднімаючи многокутники 1; 2; 3; 4; 5; 6; 7; 8; 9, отримуємо квадрат, побудований на гіпотенузі, а віднімаючи від того ж прямокутника фігури, рівновеликі тільки що переліченим (5; 6; 7 і зафарбовані прямокутники), отримуємо квадрати 8 і 9, побудовані на катетах, і доводимо, що площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів 8 і 9.

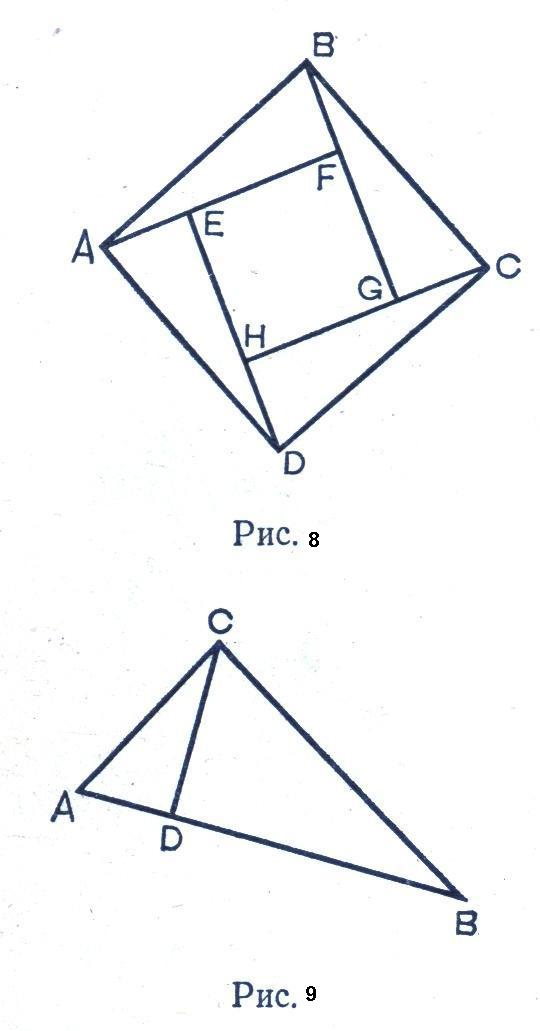
В деяких випадках при доведенні використовуються алгебраїчні тотожності. Виконавши рисунок 8 і записавши площу квадрата через його елементи, квадрат гіпотенузи (сторони більшого квадрата) виразиться через суму квадратів катетів трикутника.

На рис. 9 доведення теореми Піфагора основано на теорії подібності.

~ ∆САВ, тому (1).

∆АВС ~ ∆DCB, тому , або

(2).

Додавши (1) рівність та (2), отримаємо:

У давнину теорему Піфагора називали «віслючим мостом». Це тому, що учнів, які завчили теорему напам’ять, але не розуміли її, називали віслюками – для них вона була ніби непрохідним мостом.

Також теорему Піфагора учні називали «вітряним млином». Про теорему складали вірші такі як:

Пифагоровы штаны

Во все стороны равны,

малювали карикатури.

Задачі