Содержание

Билет № 1 2

БИЛЕТ № 2 4

БИЛЕТ № 3 10

БИЛЕТ № 4 13

БИЛЕТ № 5 15

БИЛЕТ №6 18

БИЛЕТ №7 20

БИЛET № 8 22

Билет №9. 26

Билет 10. 31

Билет 11. 34

Билет 12. 37

БИЛЕТ № 13 38

БИЛЕТ № 14 41

БИЛЕТ № 15 45

БИЛЕТ № 16 47

БИЛЕТ № 17 51

БИЛЕТ № 18 55

БИЛЕТ № 19 58

БИЛЕТ № 20 63

БИЛЕТ № 21 65

БИЛЕТ № 22 68

БИЛЕТ № 23 70

БИЛЕТ № 24 71

БИЛЕТ № 25 75

БИЛЕТ № 26 81

БИЛЕТ № 27 89

БИЛЕТ № 28 93

БИЛЕТ №29 97

БИЛЕТ № 30 101

Билет № 1

1Многоканальная смо с неограниченной очередью

Аналогично одноканальной СМО решается задача о многоканальной СМО с неограниченной очередью. Нумерация каналов:

S₀- все каналы свободны;

S₁- один канал занят, очереди нет;

S₂- занято два канала;

....................................

S_n - заняты все n каналов;

S_n+1- заняты все n каналов, одна заявка стоит в очереди;

...................................

S_n+r- заняты все n каналов, r заявок стоит в очереди;

Граф состояний многоканальной СМО с неограниченной очередью

Естественное условие существования финальных вероятностей ρ/n < 1. Если ρ/n ≥ 1, очередь растет до бесконечности.

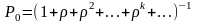
Пусть условие ρ/n < 1 выполнено. Применяя формулы для схемы гибели и размножения, найдем финальные вероятности. В выражении для P₀ будет стоять ряд членов, содержащих факториалы, плюс сумма бесконечно убывающей геометрической прогрессии со знаменателем ρ/n . Суммируя ее, найдем

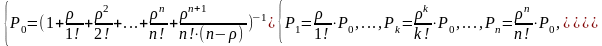
Теперь найдем характеристики эффективности СМО. Из них легче всего находится среднее число занятых каналов

выполняя соответствующие преобразования по образцу одноканальной СМО с неограниченной очередью, получим:

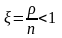
Пусть тогда

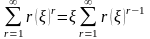
Поскольку то

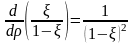
Так как то а,

Т.е.

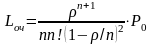
Для Lоч получим:

П рибавляя к L_оч среднее число заявок под обслуживанием (оно же - среднее число занятых каналов) получаем:

Деля, по формуле Литтла, выражение для L_сист и L_оч на λ получим средние времена пребывания заявки в очереди и в системе:

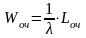
2Понятие моделирования, модели системы. Требования, предъявляемые к моделям. Виды моделей систем: черного ящика; состава системы, структуры системы; динамические.

Под моделированием системы понимают процесс создания модели, отражающей свойства системы, это способ исследования системы с помощью модели.

Модель - это объект-заместитель, воспроизводящий свойства и характеристики объекта-оригинала, имеющий по сравнению с оригиналом существенные преимущества (наглядность, обозримость, доступность испытаний и др.).

В основе моделирования лежит метод аналогий. Аналогия – подобие, сходство предметов в каких-либо признаках, отношениях. Убедившись в аналогичности двух объектов, предполагают, что функции, свойства одного объекта присущи и другому объекту, для которых они установлены.

Метод аналогий состоит в том, что изучается один объект – модель, а выводы переносятся на другой – оригинал.

Требования, предъявляемые к моделям

1. Должна описывать исследуемый объект с достаточной полнотой и обладать свойством эволюционности.

2- Должна отражать те существенные характеристики объекта-оригинала, которые необходимы для достижения, цели моделирования.

3. Должна быть достаточно простой, т.е. не содержать второстепенных связей.

4. Степень абстрактности модели должна быть допустимой по критерию получения заданной достоверности результатов исследований.

5. Должна реагировать на изменение параметров исследуемого объекта.

6. Должна обеспечивать возможность проверки ее правильности.

Модель как инструмент исследования, позволяет на основе регулирования исходными параметрами, предположениями прогнозировать поведение системы. Она является средством «упрощения» объекта, поскольку позволяет исследовать систему с точки зрения ее существенных характеристик, абстрагируясь от побочных влияний среды.

Среди методов упрощения можно назвать:

Исключение из рассмотрения ряда переменных: а) исключение несущественных; б) агрегирование;

Изменение природы переменных: а) рассмотрение переменных как констант (например, путем замены случайной величины ее математическим ожиданием); б) рассмотрение дискретных величин как непрерывных, и наоборот;

Изменение характера связи между элементами (например, замена нелинейных зависимостей на линейные);

Изменение ограничений – снятие или введение новых.

• Модель черного ящика

• Наиболее простой, грубой формой описания системы является представление ее в виде черного ящика. Такое представление не раскрывает внутренней структуры, внутреннего устройства системы.

• Любая система связана со средой и с помощью этих связей воздействует на среду, т.е. у системы есть выходы, которые отражают ее целевое предназначение.

• С другой стороны для воздействия на систему, управления ей существуют входы системы. В результате такого представления получилась модель системы, которая называется черным ящиком.

Модель состава системы

• Внутреннее содержание системы раскрывает модель состава системы.

• В структуре системы можно выделить различные элементы, подсистемы, компоненты, причем, обозначенные понятия условны. В зависимости от цели, для решения которой строится модель, один и тот же объект может быть определен и в качестве элемента, и в качестве подсистемы. В зависимости от цели исследования, постановки задачи по достижению данной цели и исходной информации, имеющейся для решения задачи, одну и ту же систему можно представлять в виде различных частей, различных иерархий.

Границы между системой и внешней средой определяются целями построения модели. Модель состава ограничивается снизу теми объектами, которые приняты в качестве элементов, а сверху - границей системы, определяемой целями анализа

• Модель структуры системы

• Модель структуры системы еще глубже характеризует внутреннюю композицию системы. Модели данного типа наряду с характеристикой состава системы отражают взаимосвязи между объектами системы: элементами, частями, компонентами и подсистемами. Таким образом, модель структуры системы является дальнейшим развитием модели состава.

• В реальных системах между объектами, входящими в их состав, имеется большое количество отношений. Отношения между элементами могут быть самыми разнообразными. Трудность состоит в том, что заранее не известно, какие отношения реально существуют, и является ли их число конечным. Задача аналитика заключается в выборе из множества реально существующих отношений между объектами, вовлеченными в систему, наиболее существенных. Критерием существенности отношений должна выступать опять же цель, для достижения которой строится модель. Таким образом, модель структуры является очередным шагом в развитии модели систем, описывающей существенные связи между элементами.

В структурных моделях абстрагируются от содержательной стороны структурных схем, уделяя внимание наличию элементов и связей между ними.

• Динамические модели систем

• Структурная модель отражает статическое состояние системы. Однако большинство задач системного анализа связано с изучением либо характеристик системы, либо с прогнозированием развития системы во времени, либо с анализом возможных траекторий развития, т.е. с изучением динамики системы, ее динамического поведения. Возникает необходимость построения новых моделей - динамических.

• Динамические модели отражают поведение систем, описывают происходящие с течением времени изменения, последовательность операций, действий, причинно-следственные связи. При построении динамических моделей на первом шаге анализируют изменения системы, которые хотят описать. Вычленяют части, этапы происходящего процесса, рассматривают их взаимосвязь. Заключительный этап построения динамической модели системы состоит в построении математического описания анализируемых процессов.