Міністерство освіти України

Луцький індустріальний інститут

Лабораторні роботи з курсу

“теорія автотранспортних засобів”

Навчально-методичний посібник

для студентів спеціальності 1505

“Автомобільне господарство”

всіх форм навчання

частина перша

Затверджено

на засіданні кафедри

автомобілів

Протокол №10 від 06.05.93.

Луцьк ЛПІ 1993

Лабораторні роботи з курсу “теорія автотранспортних засобів”. Навчально-методичний посібник для студентів спеціальності 1505 “Автомобільне господарство” усіх форм навчання. Частина перша

\ Укл. А. К. Колодійчук, В. А. Кищун, Т. І. Тернопольська – Луцьк:

ЛПІ – 45 стор.

Укладачі: Колодійчук Анатолій Констянтинович, канд. техн. наук, доцент.

Кищун Володимир Андрійович.

Торнопольська Тетяна Іванівна. канд. техн. наук. ст. викладач.

Редактор: Д. М. Коновалюк, канд. техн. наук, доцент.

Відповідальний за випуск: В. Р. Карпенко, канд. техн.

наук, доцент.

Рецензор: В. Ю. Матвієнко, канд. техн. наук, доцент.

Лабораторна робота №1

“визначення моментів інерції деталей автомобіля”

мета роботи: Визначити методику визначення моментів інерції деталей обертання.

В результаті виконання роботи студент забов’язаний:

- знати існуючі методи визначення моментів інерції

деталей обертання;

- вміти визначати аналітично і дослідним шляхом моменти

інерції заданої деталі трансмісії;

- визначити моменти інерції інших деталей автомобіля.

і. теоретичні відомості

Момент інерції деталей - величина стала і визначається її геометричними розмірами. Чим більший момент інерції деталей, тим більші інерційні моменти вона створює на валах при різних режимах обертання і тим більшу силу необхідно розвинути для розгону деталі.

Трансмісія автомобіля складається з ряду з’єднаних деталей, що обертається, моменти інерції яких суттєво впливають на динаміку розгону автомобіля. Вміння правильно розрахувати момент інерції деталей дозволяє визначити момент інерції всіх обертових частин трансмісії і таким чином частину обертового моменту двигуна необхідного для розкручування своєї трансмісія. Знання моментів інерції деталей трансмісії дозволяє також визначити:

• можливість виникнення резонансних явищ з трансмісії і розробити рекомендації для її зменшення;

• динамічні навантаження в трансмісії на перехідних режимах і вибрати обгрунтовані коофіцієнти запасу міцності.

Визначити момент інерції будь-якої деталі можна аналогічним або дослідним шляхом.

Аналітично момент інерції суцільної деталі сталого радіуса знаходиться по формулі:

де m – маса деталі, кг;

r – радіус деталі, м.

Підставивши у вище наведену формулу

M = V_ = r² l_ ,

де V – об’ем деталі, м³;

• – густина матеріалу деталі, кг/м²;

l – довжина деталі постійного радіуса, м

отримаємо:

Для сталевих, які застосовуються при конструюванні деталей трансмісії:

 = 7800 кг/м³

Тоді

І = 12,25 ^. 10³ lr⁴ ( І )

Якщо деталь має складну конфігурацію (мал.1), то її умовно розбивають на частини циліндричної форми, знаходять моменти інерції кожної, а потім останні додають (або віднімають якщо це отвір).

М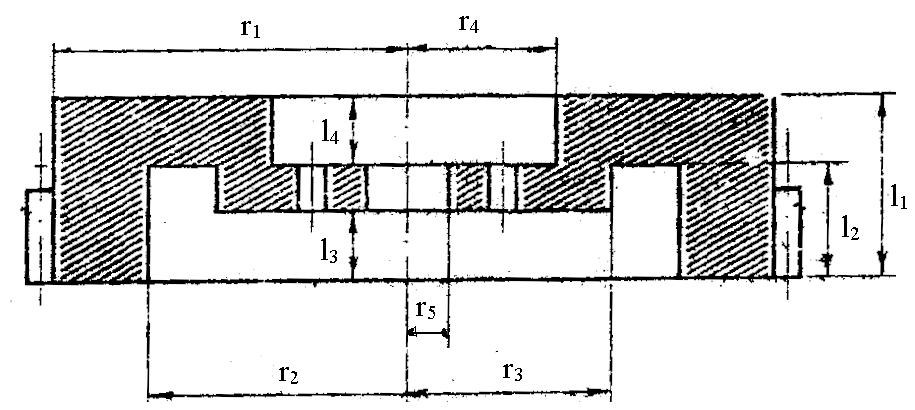 ал. 1 Ескіз маховика

Формула для визначення моменту інерції в даному випадку буде мати вигляд:

Дослідним шляхом визначити моменти інерції деталі обертання можна кількома способами. Найбільш простий з них – метод крутильних коливаннь. Для цого використовується спеціальний стенд (мал.2). Він склаладається з базового диска l, момент інерції якого І₀ відомий завчасно і дроту 2, жорстко закріпленого на верхній частині рами 3. Закрутивши диск на деякий кут, визнача-

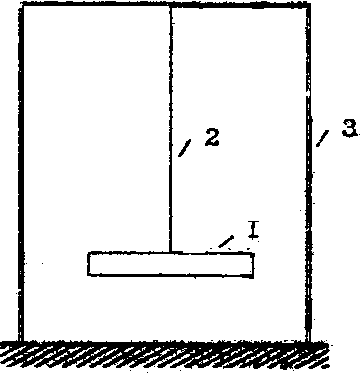ю ть період його крутильних коли- ваннь Т₀ за секундоміром. Цей же період може бути вирахований за формулою:

де І₀ – кутова жорсткість дроту

Мал.2 Схема стенда для

визначення моментів

інерції деталей обертання

Прикріпивши до диска деталь, момент інерції І_д якої необхідно знайти, аналогічним чином, за секундоміром визначають період крутильних коливаньТ свієї системи.

Ц ей же період вираховують за формулою:

Вилучивши з останніх двох рівняннь значення жорсткості k, знаходимо момент інерції всієї системи:

або момент інерції тільки деталі

(2)

Відносна похибка розрахунків моменту інерції деталі аналітичним і дослідним шляхами визначається за формулою:

(3)

де І_д – момент інерції деталі, визначиний дослідним шляхом;

І₀ – момент інерції тієї ж деталі, визначиний аналітичним шляхом.

2. Лабораторне обладнання

Опис лаборатирної установки ( мал.2 ) приведений в розділі І.

Експериментально визначаються моменти інерції для слідуючих обертальних деталей двигута і автомобіля:

а) Маховик двигуна ГАЗ-52;

б) Маховик двигуна ЗІЛ-130;

в) маховик двигуна 24Д/24-01;

г) колінвал 24Д/24-01;

д) маховик двигуна 412Э;

е) колінвал двигуна 412Э;

ж) колесо автомобіля М2138(165-13/6,45-ІЗН-14576Р);

з) колесо автомобіля ЗАЗ (5,20-13/130-330);

і) колесо автомобіля М 2140 (175/70RІЗ);

к) колесо автомобіля ГАЗ 24 (185-14/7, 35-14);

л)…………………………………………………

Вказані деталі з’єднуються з базовим диском за допомогою спеціальних кріпильних болтів. Для виконання роботи лаьораторна установка укомплектована секундоміром, лінійкою, штангельциркулем і гайковими ключами. Вказане допоміжне обладнання лаборант видає перед початком роботи.

3. Об’єм і методтика виконання роботи.

1. Виміряти діаметр і товщину базового диска і, використовуючи формулу (1), визначити (без врахування отворів) його моменти інерції І₀. Результат занести в таблицю.

2. Закрутити рукою базовий диск на кут  15…18⁰ і виміряти секундоміром тривалість 15…20 крутильних коливаннь (кількість коливаннь вказується викладачем). Визначити періоб одного коливання Т₀ і записати результат в таблицю.

3. Прикріпити до базового диска досліджувану деталь №1(один з маховиків вказаний викладачем).

4. Повтирити п. 3.2. для всієї ситеми, тобто визначити період одного коливання Т.

5. Використовуючи формулу (2), розрахувати момент інерції деталі І; результат записати в таблицю.

6. Прикріпили до базового диска вказану викладачем деталь №2 і повторити п.п. 3.4. і 3.5. результати занести в таблицю.

7. Прикріпити до базового диска вказану викладачем деталь №3 і повторити п.п. 3.4. і 3.5. результати занести в таблицю.

8. Накреслити в розрізі ескіз досліджуваного маховика, розбити його умовно на частини циліндричної форми і проставити необхілні розміри l та r.

9. Скласти формулу для визначення моменту інерції маховика аналітичним способом і знайти його значення.

10. Порівняти результат, отриманий в п. 3.5. з результатом, отриманим в п. 3.9, і за формулою (3) знайти відносну похипку визначення моменту інерції двома методами прийнявши за основу результат отриманий в п. 3.5.

Момент інерції і періоди коливаннь
Базовий диск		Деталь №1		Деталь №2		Деталь №3
Т0, С	І0,кгм2	Т1, С	І1,кгм2	Т2, С	І2,кгм2	Т3, С	І3,кгм2

* Контрольні запитання

1. Від яких параметрів залежить момент інерції деталі ?

2. Як аналітично визначається момент деталі сталого радіуса ?

3. Як аналітично визначається момент інерції однорідної деталі складної конфігурації ?

4. Назвіть експериментильні методи визначення моментів інерції деталів.

5. Як впливає момент інерції деталей трансмісії на динаміку розгону автомобіля ?

6. Як впливає момент інерції деталей на інерційні навантаження в трансмісії ?

• * *

Лабораторна робота № 2

визначення радіусів автомобільного колеса

мета роботи: засвоїти теорентичний матеріал і навчитися визначати основні радіуси автомобільного колеса

І. теоретичні відомості

При взаємодії колеса з дорогою відбувається диформація шин а також проковзування протектора відносно поверхні дороги. Тому радіус автомобільного колеса не являється постійним, а змінюється під впливом діючих на колесо сил.

у зв’язку з цим розрізняють радіуси колеса:

• вільний r_в;

• статичний r_c;

• кочення r_к;

• динамічний r_д;

Вільний радіус являє собою радіус бігової доріжки колеса, вільного від будь-якого навантаження. Він вираховується, як половина зовнішнього діаметра колеса D_з, що не навантажене зовнішніми силами (мал. 1):

r_в = 0,5^.Dз. ( І )

Якщо зовнішній діаметр невідомий, то радіус r_в можна визначити за формулою

r_в =L_k / 2. ( 2 )

де L_k – довжина бігової доріжки колеса. Деякі геометричні розміри визначаються її маркуванням, нанесеним на бічну поверхню. При маркування шини перша цифра означає ширину профілю шини В (дюймах або міліметрах),

Мал. І. Геоматричні а друга – посадочний діаметр d (в основному в дюймах). Наприклад, для шини

параметри колеса 165 80RІЗ В = 165мм; d = 13’’=13 ^. 25,4 = 330мм.

Остаточним радіусом r_c називається відстань від осі нерухомого колеса, навантаженого радіальним навантаженням, до опорної поверхні. Статичний радіус залежить від прикладеного навантаження, радіальної жорсткості шини і від твердості опорної поверхні. Цей радіус визначається безпосереднім вимірюванням, або за формулою:

r_c = d/2 =  ^. H.

Де  – коефіцієнт вертикальної деформації шини (в залежності від типу шини дорівнює ( 0,8…0,9 );

Н – висота профілю шини.

Радіусом кочення колеса r_к визначається радіус умовно жорсткого колеса, яке котиться без пробуксовування і має з даним еластичним колесом однакову кутову і лінійну швидкість.

Радіус кочення залежить від нормального навантаження на шину, тиску повітря в колесі, колової сили, коефіцієнта щеплення колеса з дорогою та швидкості руху.

Формула для визначення кадіуса кочення:

r_к = V_к / _к . ( 3 )

де V_к , _к – швидкість колеса відповідно поступальна та кутова.

Радіус кочення змінюється в широких межах, залежно від ступеня пробуксовування чи проковзування колеса:

• для буксуючого колеса V_к = 0.

• для колеса, що рухається юзом (заблокованого) _к = 0.

Іноді радіус кочення називається кінематичним радіусом. Він характеризує шлях, пройдений колесом за один оберт. З достатньою для практичних розрахунків точністю радіус кочення можна визначити також за формулою:

r_к = S_к / 2n_к . ( 4 )

де S_к – шлях, пройдений колесом;

n_к – число обертів колеса на шляху S_k.

Для стенда, показаного на малюнку 3, S_к визначається за формулою

S_к = d_ n_. ( 5 )

(тут n_ – кількість обеортів барабана 3;

d_ = 70,5мм – діаметр барабана).

Динамічний радіус колеса r_д називається відстань від осі колеса, що рухається, до опорної площини.

Динамічний радіус зменшується зі збільшенням нормального, тангенціального навантажень і зменшенням тиску повітря в шині.

Динамічний радіус залежить також від швидкості руху – зі збільшенням швидкості від дещо зростає. При русі колеса з малою швидкістю статичний і динамічний радіуси майже однакові:

r_д  r_c .

Динамічний радіус колеса, яке рухається по твердій опорі поверхні, відповідає плечу штовхаючої сили. Він може бути визначений безпосереднім вимірюванням відстані від осі рухомого колеса до дороги або за формулою:

де М_к – крутний момент на осі;

а – плече прикладення рівнодіючої нормальних сил;

Р_к – штовхаюча сила;

G_к – рівнодіюча нормальних сил.