20. Ранговые коэффициенты корреляции Спирмена и Кендалла. Особенности их вычисления при наличии связных рангов.

Коэффициент Спирмена - один из коэффициентов ранговой корреляции. Используется для измерения взаимосвязи качественных признаков, измеренных по ранговой шкале. Подсчитывается по формуле:

 

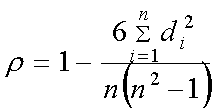
 - разность пары рангов для i – объекта, обладающего измеряемыми признаками 

n - число пар рангов 

 

Коэффициент Кендалла, как и коэффициент Спирмена, подсчитывается для признаков, измеренных по ранговой шкале, по формуле:

- определяются в вспомогательных графах таблицы сопряженности признаков, измеренных по ранговой шкале 

n - число пар рангов

Ряд объектов, упорядоченных в соответствии со степенью проявления некоторого свойства, называют ранжированным; каждому числу такого ряда присваивается ранг. Ранги обычно обозначают порядковыми числительными 1,2,…,n, где n – количество объектов. Меры взаимосвязи между парой признаков, каждый из которых ранжирует изучаемую совокупность объектов, называются коэффициентами ранговой корреляции.

Коэффициенты ранговой корреляции могут использоваться не только для анализа взаимосвязи ранговых признаков, но и при определении силы связи между ранговыми и количественными признаками, а также и между двумя количественными признаками. В таких случаях значения количественных признаков упорядочиваются и им приписываются соответствующие ранги. Существует ряд ситуаций, когда вычисление коэффициентов ранговой корреляции целесообразно при определении тесноты связи именно двух количественных признаков. Например, если связь двух количественных признаков имеет нелинейный (но монотонный) характер. Если количество объектов в выборке невелико или если для исследователя существенен знак связи, то использование корреляционного отношения   может оказаться неадекватным. Вычисление же коэффициента ранговой корреляции позволяет обойти указанные трудности.

Обычно рассматривают коэффициенты ранговой корреляции Спирмена   и Кендалла   [1, 2]. Оценка коэффициента ранговой корреляции Спирмена имеет вид:

,

где   – ранг i-го объекта в j-м наборе данных.

Оценка коэффициента ранговой корреляции Кендалла вычисляется как:

,

где   – количество инверсий в наборе данных   по отношению к  , вычисляется как

,

где

   

 

21. Понятие и классификация рядов динамики.

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называютуровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.