Среднее значение альтернативного признака и его дисперсия:

1. Среднее значение альтернативного признака

2. Дисперсия альтернативного признака

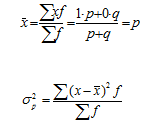
Подставив в формулу дисперсии q = 1 – p, получим:

Таким образом,  дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком.

Среднее квадратическое отклонение альтернативного признака:

Показатели относительного рассеивания

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах.  Они позволяют сравнивать характер рассеивания в различных распределениях  (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних,  при сравнении  разноименных  совокупностей). Расчет  показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к  средней  арифметической, умноженное на 100%.

1. Коэффициент  осцилляции  отражает  относительную  колеблемость крайних значений признака вокруг общей средней.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений (модуль отклонений) от средней величины.

3. Коэффициент вариации - отношение среднего квадратического отклонения к средней арифметической, применяется для сравнения вариаций различных признаков, используется как характеристика однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

16. Виды дисперсий: внутригрупповая (частная), межгрупповая и общая по правилу сложения дисперсий. Их смысл и значение. Правило сложения дисперсий, в том числе и для альтернативного признака.

Вариация признака обусловлена различными факторами, неко­торые из этих факторов можно выделить, если статистическую со­вокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В про­стейшем случае, когда совокупность расчленена на группы по од­ному фактору, изучение вариации достигается посредством исчис­ления и анализатрех видов дисперсий: обшей, меж­групповой и внутригрупповой. Ø                Общая дисперсия   измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдель­ных значений признака х от общей средней   и может быть вычислена как простая дисперсия (по формуле (5.20) или взве­шенная дисперсия по формуле (5.21). Ø                Межгрупповая дисперсия    характеризует систематиче­скую вариацию результативного признака, обусловленную влия­нием признака-фактора, положенного в основание группиров­ки. 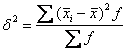Она равна среднему квадрату отклонений групповых (част­ных) средних  - от общей средней  : ,                                 где   - численность единиц в группе. Ø               Внутригрупповая  (частная) дисперсия   отражает случай­ную вариацию, т.е. часть вариации, обусловленную влиянием не­учтенных факторов и не зависящую от признака-фактора, поло­женного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы х_i,- (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно: ;                                          (5.32)                                  (5.33) На основании внутригрупповой дисперсии по каждой груп­пе, т.е. на основании   можно определить общую среднюю из внутригрупповых дисперсий :

.                       (5.34) Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

   (5.35)

Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.