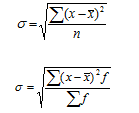15. Вариация и причины ее возникновения. Показатели вариации.

Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.

Вариация – различия значений какого-либо признака у разных единиц совокупности в один и тот же период времени.

Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.

Для измерения вариации признака используют как абсолютные, так и относительные показатели.

К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.

Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений. Определение вариации необходимо при организации выборочного наблюдения, статистическом моделировании и планировании экспертных опросов. По степени вариации можно судить об однородности совокупности, устойчивости значений признака, типичности средней, о взаимосвязи между какими-либо признаками.

Вариационный ряд (ряд распределения) – упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным значением признака.

Виды рядов распределения:

А) ранжированный – перечень отдельных единиц совокупности в порядке возрастания рассматриваемого признака.

Б) интервальный – таблица, состоящая из 2 столбцов и 2 строк, первая строка/столбец – интервал варьирующего признака (xi), вторая строка/столбец – число единиц совокупности, попадающее в данный интервал.

В) дискретный – таблица состоящая из 2 столбцов и 2 строк, первая строка/столбец – конкретное значение варьирующего признака, вторая строка/столбец – число единиц совокупности сданным значением признака.

 

К показателям вариации относятся:

I группа — абсолютные показатели вариации

• размах вариации

• среднее линейное отклонение

• дисперсия

• среднее квадратическое отклонение

II группа — относительные показатели вариации

• коэффициент вариации

• коэффициент  осцилляции

• относительное линейное отклонение

Самым элементарным показателем вариации признака является размах вариации R. Размах вариации показывает лишь крайние  (min, max) отклонения признака от общей средней.

Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.

Среднее линейное отклонение — средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической:

1. для несгруппированных данных (простое)

2. для сгруппированных данных (взвешенное)

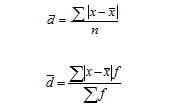
Дисперсия  признака — средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия для несгруппированных данных

2. Взвешенная дисперсия для вариационного ряда

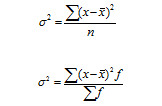
Cвойства дисперсии:

1. если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится; 

2. если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k²  раз.

Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:

где  i – величина интервала, X₁ — новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.                   

                                                                    

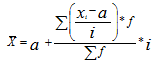
1. Момент второго порядка

2. Квадрат момента первого порядка

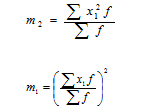
Среднее квадратическое отклонение равно корню квадратному из дисперсии:

1. для несгруппированных данных (простое)

2. для вариационного ряда по сгруппированным данным (взвешенное)

Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от ихсреднего значения.