
2.2. Вывод:
таким образом, при наличии 2-х топливозаправщиков в среднем 90,8% самолетов будут заправлены в срок, что удовлетворяет условию задачи (>85%).
2.3. Задача 2. В таблице 3 указаны статистические данные о продолжительности времени заправки летательных аппаратов топливом. Задание:
а) построить гистограмму относительных частот (частостей) и плотность распределения f(x) продолжительности заправки самолетов топливом;
б) определить математическую модель процесса заправки топливом, если промежутки времени между поступлениями требований на заправку самолетов топливом имеют экспоненциальное распределение и описываются законом: f(t) = 0,15e-0,15t;
в) подсчитать количество топливозаправщиков, которое необходимо иметь, что бы вероятность R(t) того, что время ожидания начала заправки будет меньше t=15 мин, была не менее 95%.
№ варианта |
№ таблицы |
k |
t, (мин) |
W, % |
14 |
3 |
0,1 |
19 |
85 |
Табл.3
№ обслуживания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Продолжительность заправки самолетов, мин |
16 |
18 |
17 |
23 |
15 |
15 |
25 |
16 |
22 |
17 |
15 |
20 |
22 |
23 |
18 |
№ обслуживания |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Продолжительность заправки самолетов, мин |
21 |
21 |
18 |
15 |
15 |
19 |
17 |
18 |
15 |
15 |
21 |
15 |
28 |
20 |
18 |
№ обслуживания |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
|
|
|
|
Продолжительность заправки самолетов, мин |
15 |
16 |
19 |
17 |
15 |
15 |
24 |
17 |
27 |
17 |
|
|
|
|
|
Решение
а) Построение гистограммы относительных частот (частостей) и плотности распределения f(x) промежутков времени между поступлениями требований на заправку летательных аппаратов топливом.
Ввиду того что задание а) и данные его решения задачи 1 и задачи 2 совпадают, при дальнейших расчетах возьмем данные полученные ранее в пункте а) задачи 1.
б) Определим математическую модель процесса заправки топливом.
Системы массового обслуживания характеризируют набором символов x|y|s, где х – тип потока требований, у – распределение времени обслуживания, s – число обслуживающих аппаратов.
Требования на заправку самолетов топливом образуют пуассоновский поток, который является потоком без последействия, его обозначают буквой М.
По условию задачи, время заправки распределено по экспоненциальному закону со средним значением tср.зап = 18,5 мин, поэтому данное распределение также обозначаем буквой М.
Тогда математическая модель процесса заправки самолетов топливом будет иметь вид: М|М|s.
в) подсчитаем количество топливозаправщиков, которое необходимо иметь, что бы вероятность R(t) того, что время ожидания начала заправки будет меньше t = 15 мин, была не менее W = 95%.
Из условия задачи, промежутки времени
между поступлени ями
требований на заправку самолетов
топливом имеют экспоненциальное
распределение, и описывается формулой:
f(t) = 0,15e-0,15t.
ями
требований на заправку самолетов
топливом имеют экспоненциальное
распределение, и описывается формулой:
f(t) = 0,15e-0,15t.
 Тогда
количество требований на заправку
самолетов топливом, которое поступает
за одну минуту равно (интенсивность
требований):
Тогда
количество требований на заправку
самолетов топливом, которое поступает
за одну минуту равно (интенсивность
требований):
=0,15 (1/мин)
За время tср.зап = 18,5 мин (среднее время одного обслуживания) поступает количество требований, равное:
tср.зап∙=18,5·0,15 ≈ 2,78
Следовательно, минимальное количество аппаратов, при котором пропускная способность обслуживающей системы выше интенсивности потока требований, равно 3.
Рассчитаем коэффициент загрузки для s = 3:
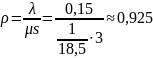
Вероятность того, что время ожидания начала обслуживания меньше t (по условию задачи t = 15 мин) рассчитывается по формуле (с учетом того, модель системы массового обслуживания имеет вид М|М|s):

R0 – вероятность того, что требованию не придется ожидать начала обслуживания. Для системы массового обслуживания вида М|М|s данная вероятность рассчитываются по формуле:
где Р0 – вероятность того, что в системе нет требований на обслуживание. Для системы массового обслуживания вида М|М|s данная вероятность рассчитываются по формуле:
Подставим данные в выше записанную формулу:

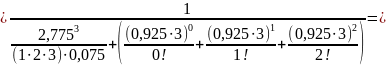

Вероятность того, что требованию не придется ожидать начала обслуживания:

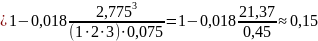
Теперь рассчитаем вероятность того, что время ожидания начала обслуживания будет меньше t = 15 мин:

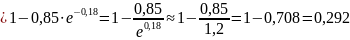
По условию задачи данная вероятность должна быть не менее 95%, а в нашем случае всего 29,2%, поэтому увеличим количество топливозаправщиков.
Проведем расчёт для s=5:
Рассчитаем коэффициент загрузки:

Подставим данные задачи в приведенные формулы:
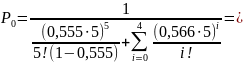



Вероятность того, что требованию не придется ожидать начала обслуживания:


Тогда:


