Багатоелектронні атоми

Одержати точний розв’язок рівняння Шредінгера для багатоелектронної системи неможливо бо електрон рухається не в центральному полі одного ядра, а в полі ядра та останніх електронів (остова атома). Як раз міжелектронне відштовхування не дозволяє точно розв’язати рівняння.

Нині найбільш широко з усіх наближених методів такого врахування застосовується одноелектронне наближення руху електрона, метод самоузгодженого поля, метод Хартрі - Фока. За цим методом хвильова функція атома представляє собою добуток самоузгоджених одноелектронних хвильових функцій, що описують кожний із електронів в полі ядра і усіх останніх електронів (АО Хартрі).

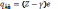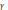Реальний потенціал, діючий на даний електрон, можна замінити сумою потенціала ядра і усерекдненого потенціала останніх n-1 електронів. Ефективний заряд остова ( де Z-пopядкoвий номер елемента в періодичній системі, – коефіцієнт екранування, показує наскільки заряд ядра, діючий на даний електрон, нейтралізується останніми електронами ). Поле, створене атомним остовом, хоча і не кулонівське, має центральну симетрію, як і поле ядра у воднеподімному атомі. Тому і в розглядаємому випадку квантові числа n і I зберігають своє значення. Але на відміну від воднеподібного атома енергія електрона залежить не тільки від n, а і від I, бо енергія електрона залежить від того, як він поляризує остов атома (порушує його центральну симетрію) і як він проникає в середину остова. Поляризація ж і проникнення залежать від типу орбіталі АО, т.б. від орбітального квантового числа I.

Найбільш „проникаючими” у даному квантовому шарі є s - орбіталі, так як їх максимуми лежать ближче всього до ядра; в ряду s-, р-, d-, f-підрівней „проникнення” зменшується. Тому в даному шарі більш зв’язані з ядром є s-, потім р-електрони і т. д. У електронному шарі з даним головним квантовим числом n електрони розрізняються по енергії в залежності від того до якого із підрівней вони належать. Відмінності зростають із збільшенням заряду ядра. Т. чином, виродження відносно квантового числа I у багатоелектронному атомі знімається.

Взаємний вплив електронів один на одного в багатоелектронних атомах обумовлює зміну послідовності зростання енергії орбіталей в порівнянні з послідовністю у воднеподібних системах.

На основі вивчення спектрів атомів і квантово-механічних розрахунків встановлена така послідовність енергетичних підрівнів у багатоелектронних атомах

1s<2s<2р<Зs<Зр<4s<Зd<4р<5s<4d<5р<бs<4f<5d<6р<7s<5f 6d<7р .

Для запам’ятовування послідовності АО зручно користуватися емпіричним правилом Клечковського (Маделунга): АО слідують у послідовності зростання суми кв. чисел ( n+1); при чому, у групі рівней з однаковим значенням n+1 першими слідують рівні з меншим значенням n .

(Слід відмітити, правило є наближеним).

Квантово-механічні розрахунки показують, що кожний енергетичний рівень багатоелектронного атому розщеплюється на таке число енергетичних підрівнів, скільки видів орбіталей включає цей рівень.

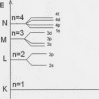
Послідовність заповнення електронами енергетичних рівнів, підрівнів у багатоелектронних атомах

В основі лежать 2 фундаментальних принципи і одно правило:

1. Принцип заборони Паулі (швейцарський фізик Вольфганг Паулі (1900-1958 р.) ) - в атомі не може бути 2-х електронів , які характеризуються однаковим набором усіх 4-х квантових чисел.

( Принцип Паулі пов’язаний з фундаментальним принципом квантової механіки – про неможливість розпізнати тотожні частинки у мікросвіті. Електрони - ферміони).

2. Принцип мінімуму внутрішньої енергії ( довільна система намагається досягати стану з min - ним запасом внутрішньої енергії).

При виконанні цих принципів діє

правило Хунда (Гунда) (німецький фізик Ф. Хунд, 1927 р.) - заселення електронами орбіталей даного підрівня відбувається так, щоб їх сумарний спін був максимальним:

а) під час заповнення підрівня електрони посідають різні орбіталі доти, поки це можливо;

б) спіни поодиноких електронів на різних орбіталях паралельні.