Квантовані стани атома

Завдяки малим розмірам і великій масі ядро атома можна наближено вважати точковим, що знаходиться в центрі мас атома і розглядати атом як систему електронів, які рухаються навколо нерухомого центра - ядра. Повна енергія такої системи Е = сумі кінетичної енергії всіх електронів і потенціальної енергії, яка складається із енергії притягання електронів ядром і енергії взаємного відштовхування електронів один від одного. Атом підпорядковується законам квантової механіки; його основна характеристика як квантової системи - повна енергія Е може приймати лише одне із значень дискретного ряду E₁<E₂<E₃<... . Кожному із „дозволених” значень Е_i відповідає один або декілька стаціонарних (незмінних з часом) станів атома. Енергія Е може змінюватися тільки стрибкоподібно - шляхом квантового переходу атома із одного стаціонарного стану в другий.

Методами квантової механіки можна точно розрахувати Е для одноелектронних атомів - воднеподібних систем.

Воднеподібні системи

H,He⁺,Li⁺⁺

Стан електрона у воднеподібному атомі описується хвильовою функцією Ψ, яка є розв’язком стаціонарного рівняння Шредінгера :

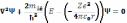
Не вдаючись до математичного розв’язання цієї задачі, обмежимось розглядом лише її важливих результатів.

1. Енергія

Рівняння Шредінгера має розв’язки , що зодовольняють вимогам однозначності, скінченності і неперервності хвильової функції ϕ лише при дискретних (власних) значеннях енергії

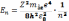, (n=1,2,3,…)

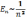. (див. Рис.)

2. Квантові числа

Рівняння Шредінгера задовольняють власні хвильові функції Ψ=Ψ_{n,I,mI ,} які

визначаються трьома квантовими числами:

головним n;орбітальним I ;магнітним орбітальним m_I. ( вони зв’язані).

Головне квантове число, n

n -визначає середню відстань від ядра до ділянки підвищеної електронної густини, т.б. розміри електронної хмари та загальну енергію електрона на даному рівні; може набувати додатні цілочислові значення п = 1,2,3,4,...,∞.

Стан електрона , який характеризується певним n, називають енергетичним рівнем електрона в атомі. Для енергетичних рівнів електрона в атомі прийняті латинські позначення

Головне квантове число	1	2	3	4	5	6	7
Енергетичні рівні	К	L	M	N	O	Р	Q

Max кількість енергетичних рівнів, яку може мати атом в основному стані, відповідає номеру періоду, в якому розміщений даний хім. елемент.

Орбітальне квантове число, І

Тонка структура лінійчастих спектрів (мультиплетність) (складаються з кількох близько розміщених ліній, які відповідають переходу електрона з одного енергетичного рівня на інший) вказує на різні квантовані стани електрона на певному енергетичному рівні, що зумовлено різною формою електронних орбіталей. От же, основні енергетичні рівні складаються з певного числа енергетичних підрівнів.

Для характеристики енергії електрона на підрівні та форми електронних орбіталей, введено орбітальне квантове число I.

З розв’язків рівняння Шредінгера випливає, що орбітальний момент імпульсу електрона L_I квантується. Його модуль не може бути довільним, а набуває дискретних значень

,

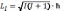при заданому n I набуває стільки ж значень I = 0, 1, 2,..., (n-1).

Кожному I відповідає певний енергетичний підрівень

Орбітальне квантове число, I	0	1	2	3
Енергетичний підрівень	s	р	d	f

( Буквені позначення підрівнів відповідають першим буквам англійських назв відповідних спектральних ліній, що виникають внаслідок електронних переходів , відповідно до значень I

sharp -різка; principal -ocновнa;diffus -дифузна; fundamental -фундаментальна ).

Можлива кількість підрівнів для даного енергетичного рівня п рівна номеру цього

рівня.

Магнітне орбітальне квантове число, m_I,

У магнітному полі спектральні лінії атомів стають ширшими або розщепляються (з’являються нові близько розташовані лінії), збільшується мультиплетність. Це пояснюється тим, що електрон в атомі на всіх підрівнях(крім s -підрівня) характеризується крім орбітальним ще й магнітним орбітальним моментом. ( див. Рис.) Енергетичні зміни, які при цьому відбуваються , можна пояснити різним розміщенням електронних орбіталей у просторі, яке характеризується m_I.

Магнітне поле орієнтує площину електронної орбіталі у просторі під певними кутами ( відбувається просторове квантування), при яких проекція орбітального моменту імпульсу L_Iz на напрямок зовнішнього поля набуває квантованих значень кратних ħ

L_IZ=m_I·ħ

де m_I = 0, ±1,±2, … ,±I.

Т.б. всього може прийняти (2I+1) можливих орієнтації

При даних n і I може бути декілька станів електрона з однаковою енергією. Такі стани називають виродженими.

Тому:

s - стан вироджено 1 раз, бо I= 0 m_I має 1 значення

р - стан вироджено 3 рази, бо I=1 m_I має 3 значення

d - стан вироджено 5 разів, бо I=2 m_I має 5 значень

f - стан вироджено 7 разів, бо I=3 m_I має 7 значень

За характером орієнтації у просторі

р- орбіталі позначають P_x, P_y, P_z;

d-орбіталі

f - орбіталі мають ще складнішу форму. (див. Рис.)

Число різних станів, що відповідає даному n

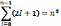
Квантові стани електронів; ємність рівнів, підрівнів електронних оболонок

Досліди Штерна і Герлаха. Спін електрона. Спінове квантове число.

У дослідах по вимірюванню магнітних моментів атомів елементів ІА гр., у яких валентний електрон не має орбітального моменту імпульсу ( I = 0 ), а отже відсутній і орбітальний магнітний момент ( m_I=0 ) німецькими фізиками О. Штерном і В. Герлахом у 1921 в неоднорідному магнітному полі було встановлене просторове квантування. Цей експериментальний факт у 1925 р. 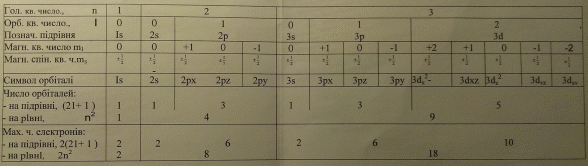пояснили американськи вчені Гаудсміт і Уленбек наявністю у електрона власного моменту імпульсу ( спіну, 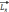) та зв’язаному з ним власного магнітного моменту .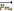

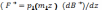; - неможна дати наочної класичної інтерпретації, це чисто квантова характеристика частинки. Разом з масою й зарядом спін є важливішою постійною частинки. Він характеризує не тільки електрон, але й протон, нейтрон, фотон та інші частинки).

Модуль власного моменту імпульсу квантується по закону

s - спінове квантове число,

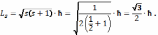
Проекція спіна на напрямок зовнішнього магнітного поля є квантованою величиною та визначається

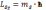, m_s - магнітне спінове квантове число,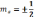 .