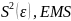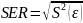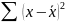7. Точечный и интервальный прогнозы для модели парной линейной регрессии

Одной из задач эконометрического моделирования выступает прогнозирование социально-экономических явлений и процессов. Эта задача может решаться на основе регрессионных моделей, с помощью которых прогнозируется поведение результативной переменной в зависимости от поведения факторных переменных, включенных в модель.

Точечный прогноз значения результативной переменной ( ) при заданном значение факторной переменной (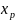 ) будет определяться по формуле:

При этом действительная величина будет определяться как:

Таким образом, истинное значение результативной переменной будет отклоняться от расчетного значения под влиянием ошибок параметров модели и случайной ошибки регрессии.

Запишем модель регрессии, используемую для прогнозирования, в следующем виде:

Отсюда следует, что стандартная ошибка регрессии в точке зависит от стандартной ошибки результативной переменной и стандартной ошибки коэффициента регрессии :

Теоретическое значение (математическое ожидание) результативной переменной в точке с вероятностью будет находиться в интервале, определяемом как:

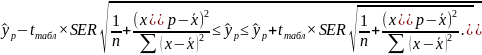
В свою очередь, ошибка истинного значения результативной переменой будет зависеть от ошибки регрессии в точке и дисперсии ошибок регрессии:

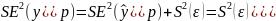
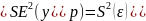
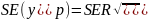
Таким образом, истинное значение результативной переменной в точке с вероятностью будет находиться в интервале, определяемом как:

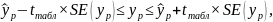
Другими словами 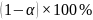фактических значений результативной переменной в генеральной совокупности будут находиться в пределах указанного интервала.

Из приведенных формул мы видим, что ошибка как теоретического, так и фактического значения результативной переменной зависят от трех параметров:

1. Значение стандартной ошибки регрессии 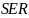. Стандартная ошибка регрессии представляет собой корень из остаточной дисперсии на одну степень свободы. Следовательно, чем выше качество регрессионной модели, тем точнее сделанный по ней прогноз.

2. Отклонение точки для которой рассчитывается прогнозное значение от среднего значения факторной переменной. Чем ближе к , тем точнее прогноз. Максимальная точность достигается в точке 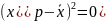, то есть .

3. Дисперсии факторной переменной. Чем больше дисперсия x при фиксированном числе наблюдений, тем точнее прогноз зависимой переменной.

Пример 2.12. Рассмотрим пример нахождения доверительных интервалов для построенной нами модели парной линейной регрессии, описывающей зависимость оборота розничной торговли от доходов населения.

Необходимо найти прогнозное значение оборота розничной торговли на душу населения в регионе, при заданной величине среднедушевых денежных доходов населения 15,6 тыс. руб.

Занесем исходные данные в таблицу 2.7.1.

Таблица 2.7.1

Исходные данные для прогнозирования оборота розничной торговли

№ п/п	Показатель	Значение	Источник
1		0,34	Таблица 2.6.2
2		0,58	Расчет
3		31,19	Таблица 2.6.3
4		13,9	Таблица 2.2.1
5		15,6	Исходные данные
6	n	16	Исходные данные
7		2,14	Таблица распределения Стьюдента

Теоретическое значение оборота розничной торговли на душу населения при среднедушевых доходах населения в размере 15,6 тыс. руб. составит:

Найдем 95% доверительные интервалы для этого значения:

Таким образом, в 95% выборок (и соответственно в построенных по этим данным моделях регрессии) прогнозное значение оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб. будет находиться в пределах от 7,6 тыс. руб. до 8,5 тыс. руб.

Определим 95% доверительные интервалы для фактического значения оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб.:

Следовательно, с вероятностью 0,95 мы можем утверждать, что фактическое значение оборота розничной торговли при среднедушевых доходах населения в размере 15,6 тыс. руб. будет находиться в пределах от 6,8 тыс. руб. до 9,4 тыс. руб.

Рассмотрим графическое изображение найденных доверительных интервалов значений результативной переменной (рис. 2.7.1).

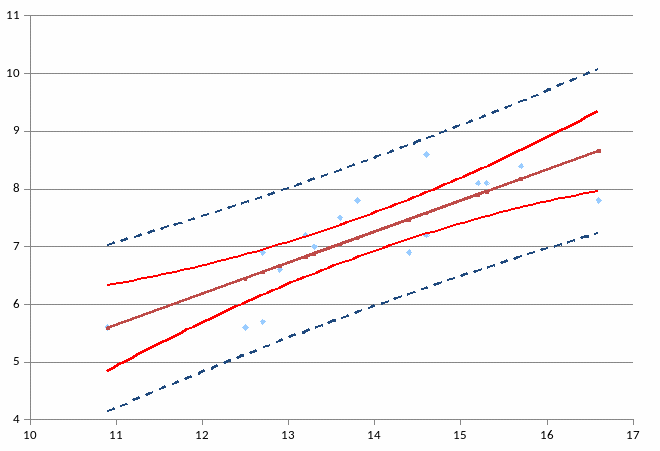
Линия регрессии

Доверительный интервал для линии регрессии

Рис. 2.7.1. Доверительные интервалы для теоретических и фактических значений результативной переменной

(оборота розничной торговли на душу населения)

На рисунке 2.6.1 мы видим, что границы доверительных интервалов расширяются по мере удаления от центра распределения факторной переменной. При этом все фактические значения оборота розничной торговли на душу населения попадают в 95% доверительный интервал.