4. Предпосылки мнк при оценивании параметров модели регрессии
Для того чтобы оценки параметров модели регрессии полученные с использованием МНК обладали свойствами состоятельности, эффективности и несмещенности необходимо соблюдение ряда предпосылок или допущений МНК.
Первые предпосылки формулируются относительно природы исходных данных:
Истинная форма зависимости между результатирующей переменной y и факторной переменной x является линейной.
Факторная переменная x является нестохастической (неслучайной), то есть в анализе используется фиксированный набор ее значений.
Предположение
о нестохастической природе факторной
переменной означает, что в ходе
контролируемого эксперимента при одном
и том же наборе значений переменной x
будут
получены различные наборы значений
случайной ошибки
и, следовательно, различные наборы
значений результативной переменной y.
На практике нарушение предпосылки о нестохастической природе факторной переменной чаще всего возникает в ходе проведения статистического наблюдения за исследуемыми переменными.
Рассмотрим
ситуацию, когда переменная x
является стохастической переменной
вследствие возникновения ошибки
наблюдения
.
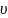Пусть наблюдаемое значение факторной
переменной x
складывается
из истинного значения исследуемого
признака
и ошибки измерения
:
тогда
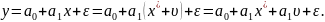
В
силу тождества
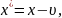между x*
и
существует
зависимость,
что делает МНК-оценки параметров
рассмотренной модели смещенными и
несостоятельными. Причины этого явления
будут рассмотрены нами в разделе
посвященном изучению проблемы
мультиколлинеарности.
Вторая группа предпосылок МНК формулируется относительно свойств случайных ошибок модели регрессии:
1. Математическое ожидание (средняя величина) случайных ошибок модели регрессии равно 0:
Для
модели регрессии содержащей свободный
член данная предпосылка никогда не
нарушается. Если теоретическое обоснование
модели требует приравнивания свободного
члена к нулю, то есть перехода к
регрессионной модели вида
,
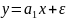то несоблюдение рассматриваемой
предпосылки ведет к существенному
смещению оценки параметра
.
Дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
Учитывая, что регрессионные остатки представляют собой выборочные оценки случайной ошибки модели, говорят о гомоскедастичных остатках или гомоскедастичности, когда остатки имеют одинаковую дисперсию, и о гетероскедастичных остатках или гетероскедастичности – когда дисперсия остатков различна.
Примеры отображения гетероскедастичных и гомосскедастичных остатков на диаграмме рассеяния представлены на рисунке 2.4.1.
Рис. Примеры гетероскедастичности (A-C) и гомоскедастичности (D) остатков
Гетероскедастичность остатков ведет к смещению стандартных ошибок параметров модели регрессии, что затрудняет проверку их статистической значимости.
3. Ковариация между значениями случайной ошибки для любой пары наблюдений равна 0:
Нарушение данной предпосылки называют автокорреляцией случайной ошибки или автокорреляцией остатков. Данная проблема возникает при построении моделей регрессии по данным, представленным в виде временных рядов. Автокорреляция остатков, как и их гетероскедастичность обуславливает смещение стандартных ошибок параметров модели регрессии.
4. Случайная ошибка и факторная переменная x независимы друг от друга:
Данная предпосылка представляет собой частный случай допущения о нестохастической природе факторной переменной. В случае несоблюдения предпосылки говорят о проблеме эндогенности. При этом МНК-оценки параметров регрессии являются несостоятельными и смещенными:
Учитывая,
что
=0,
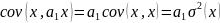получим:
Таким
образом при
,
а следовательно
не выполняется условие несмещенности
оценки параметра