Проверка устойчивости принятого сечения двутавра в плоскости рамы.

_{Предельно допустимая гибкость}

Проверяем устойчивость подкрановой ветви колонны из плоскости рамы:

Устойчивость подкрановой ветви колонны в плоскости рамы обеспечена.

3. Подбор сечения наружной ветви колонны

Определяем ориентировочно требуемую площадь сечения ветви колонны.

где,



коэффициент устойчивости, которым сначала следует задаться ориентировочно в пределах 0,6…0,8;

Ширина листа b_л принимается на 50 мм меньше высоты сечения двутавра подкрановой ветви.

Рис. 2.4. Схема компоновки сечения наружной ветви колонны

Принимаем лист с размерами сечения:

Определяем требуемую площадь поперечного сечения уголков:

Принимаем два равнополочных уголка № 160* х16: A_уг = 49,1 см²,

I_x = 1175 см⁴, z₀ = 4,55 см.

Определяем скомпонованную площадь сечения наружной ветви колонны:

Уточняем привязку оси x₂ наружной ветви колонны к её наружной грани:

Определяем моменты инерции сечения наружной ветви колонны относительно осей Y и X₂:

Вычисляем радиусы инерции ветви колонны:

Определяем гибкости ветви колонны:

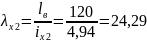
Проверяем устойчивость наружной ветви колонны:

- из плоскости рамы

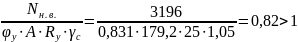
- в плоскости рамы

Проверки не выполняются.

Уменьшаем толщину листа и сечение уголков.

Принимаем лист с размерами сечения:

Принимаем два равнополочных уголка № 160 х14: A_уг =43,3 см², I_x = 1046 см⁴, z₀ = 4,47 см.

Определяем скомпонованную площадь сечения наружной ветви колонны:

Уточняем привязку оси x₂ (рис. 1.4) наружной ветви колонны к её наружной грани:

Определяем моменты инерции сечения наружной ветви колонны относительно осей Y и X₂:

Вычисляем радиусы инерции ветви колонны:

Определяем гибкости ветви колонны:

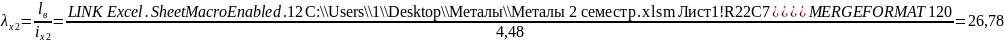
Проверяем устойчивость наружной ветви колонны:

- из плоскости рамы

- в плоскости рамы

Условия выполняются, устойчивость наружной ветви колонны в плоскости и из плоскости рамы обеспечена.

4. Расчет соединительной решетки ветвей колонны

Расчет элементов соединительной решетки стержней составного сечения необходимо выполнить, как для элементов плоских ферм.

_{подбор элементов решетки выполняем по} .

Для решетки (рис. 1.4.2. [1]) усилия в раскосе определяется по формуле:

где,		условная поперечная сила, приходящаяся на одну плоскость решетки, ;
		коэффициент, для треугольной решетки β=1;
		длина раскоса;
		сечение нижней части колонны;

Находим требуемую площадь сечения раскоса:

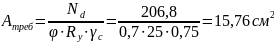
где,		коэффициент условий работы, ;
		задается в пределах 0,7…0,9;

Принимаем равнополочный уголок № 110 х 8: A_d = 17,20 см², i_y0 = 2,18 см⁴.

Определяем расчетную длину раскоса, гибкость раскоса и условную гибкость раскоса:

Производим проверку устойчивости раскоса:

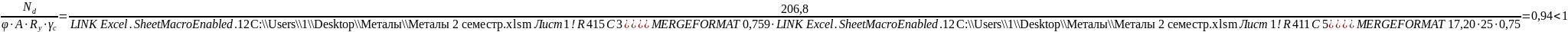Проверка выполняется.

Стойки соединительной решетки (рис. 2.2) рассчитываем на условную поперечную силу .

Определяем требуемый радиус инерции сечения стойки:

По значению требуемого радиуса инерции из сортамента выбираем равнобокий уголок при условии, что радиус инерции уголка .

Принимаем равнополочный уголок № 50 х5: А = 4,8 см i_y0 = 1,53 см.

Проверка выполняется.