Волны типа в круглом волноводе.

Для волн составляющие поля в круглом волноводе описываются выражением

В выражении 44 так же как и в выражении …… подрузамевается множитель ……… Причем для случая в круглых волновода . Граничные условия для волн типа в круглом волноводе определим из общих граничных условий, а именно около проводящей поверхности тангенциальная составляющая электрического поля должна быть равна 0 т.е. . Критерием простейшей волны в волноводе является не обращение в 0 продольной составляющей а именно для данного случая. Из выражения 44 следует, что простейшими волнами в круглом волноводе могут быть волны типа . Согласно граничным условиям при r=a, E_z=0 . Для волн типа где это n-ый корень функции Бесселя нулевого порядка. Таким образом критическое волновое число будет равно . С учетом выражения 43 найдем критическую длину волны. . Как видно из графиков функции Бесселя Рис.24 наименьшее значение корня для функции Бесселя 0-го порядка получается при n=1 и составляет , таким образом из волн типа наибольшей критической длиной волны равной обладает волна . Для волн составляющие поля будут определятся выражениями:

Структура электромагнитного поля волны в круглом волноводе приведена на Рис.25, на Рис.26 приведено распределение токов на внутренней поверхности стенки волновода.

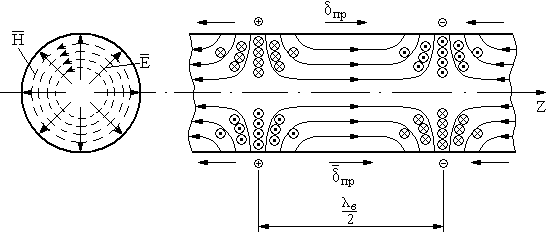
Рис. 25. Структура электромагнитного поля волны E₀₁ в круглом волноводе

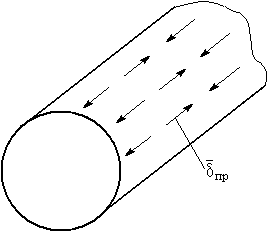
Рис. 26. Распределение токов проводимости на внутренней поверхности стенок круглого волновода для волны E₀₁

Из Рис.25 и Рис.26:

Магнитное поле представляет собой окружности расположенные в поперечной плоскости.
Электрическое поле волны представляет собой полупетли начинающиеся и заканчивающиеся на стенке волновода и вытянутые вдоль оси Z.
Заряды на стенках волновода порождают токи проводимости протекающие в направлении т.е. продольные токи.
Отсутствие поперечных токов проводимости приводит к уменьшению волнового сопротивления.

dfsdfs

Учитывая что структуры ДОПИСАТЬ ДОПИСАТЬ близки между собой можно строить переходы с одного сечения на другое практически без преобразования волн и следовательно с минимальными потерями (вращающиеся сочленения). Для волн типа коэфициент затухания определяется выражением . Предельная мощность пропускаемая волноводом с волной определяется соотношением допустимая передаваяемая мощность определяется из выражения 9.

Волны типа в круглом волноводе.

Для волн составляющие поля в круглом волноводе определяются выражениями.

Выражение 50 так же как и в случае волн типа для краткости опущен множитель . Граничные условия в круглом волноводе определим из общих граничных условий, а именно около проводника нормальная составляющая вектора напряженности магнитного поля должна быть равна 0, т.е. . Как уже отмечалось критерий простейшей волны в волноводе является не обращение в 0 продольных составяющих а именно для данного случая. Из выражения 50 следует что простейшими волнами в круглом волноводе будут волны типа . Согласно граничным условиям из выражения 50 если . является производной функции бесселя первого рода нулевого порядка. Откуда мы получаем где -ДОПИСАТЬ. Для нахождения воспользуемся соотношением . Из соотношения 51 следует что . Таким образом критическое волновое число будет равно . Критическая длина волны с учетом выражения 43 будет равна . Как видно из графиков функции Бесселя наименьшее значение корня а следовательно и получается при . Таким образом для волны с наименьшими индексами m и n критическая длина волны будет равна . Для волны составляющие поля будут определяться выражениями: