- •Лекция 1. Основные понятия свч устройств.
- •Лекция 2. Линии передачи свч.
- •Коаксиальные линии. Основные понятия.
- •Лекция 3. Стандарты и конструкции.
- •Гибкие коаксиальные линии (кабель).
- •Жесткие конструкции коаксиальных линий.
- •Конструкция с металлическими стержнями.
- •Конструкция с диэлектрическими шайбами.
- •Лекция 4.
- •Прямоугольный волновод. Основные понятия.
- •Граничные условия для векторов электрического поля.
- •Граничные условия для векторов магнитного поля.
- •Волны типа Hmn в прямоугольном волноводе.
- •Лекция 5.
- •Волны типа Emn в прямоугольном волноводе.
- •Лекция 6.
- •Круглый волновод. Основные понятия.
- •Волны типа в круглом волноводе.
- •Волны типа в круглом волноводе.
- •Лекция 7.
- •Соединение элементов линий передач. Соединители линий передач. Основные понятия.
- •Фланцевые соединения с бронзовыми рассеченными прокладками.
- •Фланцевые соединения с бронзовой контактной прокладкой «коробочка».
- •Дроссельно-фланцевые соединения.
- •Соединители кл. Коаксиальные разъемы.
- •Лекция от 08,05,2013 Дроссельные соединения.
- •Одинарные дроссельные соединения коаксиальной линии.
- •Двойное дроссельное соединения коаксиальной линии.
- •Изгибы линии передач. Изгибы волноводных линий.
- •Изгибы коаксиальных линий.
- •Лекция от 15,05,2013
- •Переходы между линиями передач различных типов.
- •Переходы между прямоугольным и круглым волноводами.
- •Коаксиально-волноводные переходы квп.
- •Ортогональные квп.
- •Зондовые квп
- •Квп с последовательным шлейфом
- •Квп с поперечным стержнем
- •Квп «пуговичного» типа
- •Лекция от 22,05,2013 Соосные квп
- •Элементы свч устройств Согласованные нагрузки для линий передач. Общие сведения.
- •Согласованные нагрузки коаксиальных линий.
- •Согласованные нагрузки волноводных линий.
Волны типа Emn в прямоугольном волноводе.
Решение
мембранного уравнения (16) для волн типа
Еmn имеет вид
Для рассчетов
поперечных составляющих вектора
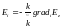 где
где
 определяются из выражений (21), (22), (26)
соответсвенно
определяются из выражений (21), (22), (26)
соответсвенно
Из соотношения
32 проекции поперечной составляющей
вектора напряженности электрического
поля будут иметь вид

Лекция 6.
В выражениях
(31) и (33) так же как и в случае волн
 для краткости опущен множетель
для краткости опущен множетель
 .
Проекции поперечной сотавляющей
магнитного поля можно найти из проекций
вектора напряженности электрического
поля (33) по закону Ома
.
Проекции поперечной сотавляющей
магнитного поля можно найти из проекций
вектора напряженности электрического
поля (33) по закону Ома
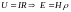 (в законе Ома У и H должны
быть перпендикулярны)
(в законе Ома У и H должны
быть перпендикулярны)

 -
волновое сопротивление пряямоугольного
волноводас данными поперечными размерами
на данной частоте для волн типа
-
волновое сопротивление пряямоугольного
волноводас данными поперечными размерами
на данной частоте для волн типа
 .
.
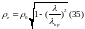 .
Из выражения 35 очевидно что
.
Из выражения 35 очевидно что
 .
Как видно из выражения 31 для волн типа
ни один из индексов m или
n не может быть равен 0.
Следовательно для волн
минимальными значениями индексов могут
быть
.
Как видно из выражения 31 для волн типа
ни один из индексов m или
n не может быть равен 0.
Следовательно для волн
минимальными значениями индексов могут
быть
 и мледовательно простейшей волной
данного типа будет волна
и мледовательно простейшей волной
данного типа будет волна
 .
Для волны
имеем:
.
Для волны
имеем:
На Рис.21
приведена структура электоромагнитного
поля волны
 в прямоугольном волноводе.
в прямоугольном волноводе.
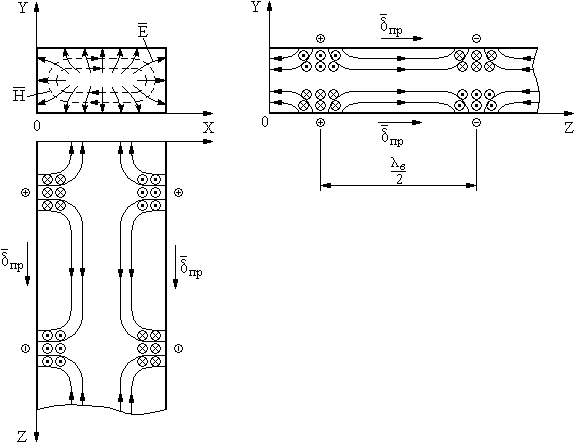
Рис. 21. Структура электромагнитного поля волны E11 в прямоугольном волновод
Из рисунка 21 видно что:
Структура волны содержит полупетли эл.поля ДОПИСАТЬ
Магнитное поле является петлевым в плоскости Х0У.
В плоскости Х0У образуются стоячие волны
В направлении Z существует бегущая волна поскольку максимум электрического поля совпадает с максимумом магнитного поля распределенного вдоль оси Z.
Заряд на стенках волновода пораждает токи проводимости протекающие только в направлении
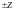 то есть продольные токи (Рис.22).
то есть продольные токи (Рис.22).Отсутствие поперечных токов приводит к уменьшению волнового сопротивления.
Из Рис.21 хорошо видно что распределение электромагнитного поля волны относительно осей Х и У практиччески одинаково. Поэтому имеет смысл размеры волновода а и b брать одинаковые, это практически всегда выполняется на практике. При этом:
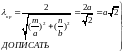
Из выражения 36 следует что для данного случая так же как и для волны длина волны в волноводе возрастает.
Исходя из выражений 35 и 36 выбирается таким образом что бы было бы равно 200 Ом.
Это
в свою очередь и определяет размеры
волновода а. наличае токов проводимости
на стенках волновода приводит к затуханию
волны
.
При этом коэффициент затухания
определяется по формуле

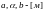
 -
удельная проводимость материала
волновода
-
удельная проводимость материала
волновода
Предельная
мощность пропускаемая волнводом с
волной
определяется выражением
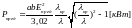 где
где
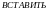
-
предельная напряженномть диэлектрика
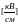
Допустима передааваемая мощность так же как и в случае для коаксиальной линии определяется из выражения 9
Круглый волновод. Основные понятия.
Круглые волноводы наряду с прямоугольными получили достаточно широкое применение. Например, отрезки круглого волновода применяются как элементы вращающихся сочленений предназначенных для передачи электромагнитной энергии от неподвижных волноводов к подвижным, кроме того отрезки круглого волновода могут использоваться как облучатели антенн. Закороченный с двух сторон отрезок круглого волновода применяется как электро магнитный резонатор. Так как фактически круглый волновод является цилиндрической направляющей системой то для описания составляющих электромагнитного поля в нем применяется цилиндрическая система координат (Рис.23).
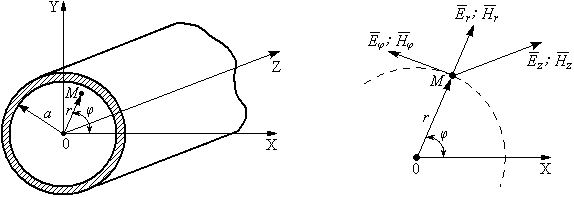
Рис.
23. Круглый волновод в цилиндрической
системе координат:
 -
тангенциальные составляющие векторов
электрического и магнитного полей;
-
тангенциальные составляющие векторов
электрического и магнитного полей;
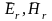 -
нормальные составляющие векторов
электрического и магнитного полей;
-
нормальные составляющие векторов
электрического и магнитного полей;
 -
продольные составляющие векторов
электрического и магнитного полей
-
продольные составляющие векторов
электрического и магнитного полей
В круглых
волноводах так же как и в прямоугольных
могут существовать волны
 .
Продольные составляющие векторов
напряженности электромагнитного поля
(
.
Продольные составляющие векторов
напряженности электромагнитного поля
( ) так же будут являтся решением мембранного
уравнения но в цилиндрической системе
координат.
) так же будут являтся решением мембранного
уравнения но в цилиндрической системе
координат.
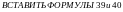
Поскольку
распределение по
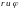 независят друг от друга то выражения
для продольных составляющих векторов
напряженности магнитного и электрического
полей можно выразить через функции
Бесселя.
независят друг от друга то выражения
для продольных составляющих векторов
напряженности магнитного и электрического
полей можно выразить через функции
Бесселя.
 где,
где,
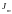 -
функция Бесселя первого рода m-го
порядка
-
функция Бесселя первого рода m-го
порядка
 -критическое
волновое число
-критическое
волновое число

По известным
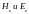 используя приведенное ранее соотношение
электродинами (20) можно рассчитывать
остальные составляющие поля. При
некоторых значениях r
составляющие
могут обращаться в 0. Из этого условия
при
используя приведенное ранее соотношение
электродинами (20) можно рассчитывать
остальные составляющие поля. При
некоторых значениях r
составляющие
могут обращаться в 0. Из этого условия
при
 рассчитываются корни функции Бесселя.
Примеры граффиков функции Бесселя
приведены на (Рис.24)
рассчитываются корни функции Бесселя.
Примеры граффиков функции Бесселя
приведены на (Рис.24)
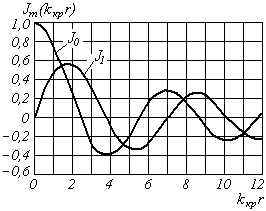
Рис. 24. Функции Бесселя 0-го и 1-го порядка
Из графиков на Рис.24 вытекает математический смысл индексов m и n волн . Индекс m показывает порядок функции Бесселя и определяет число стоячих волн поля укладывающихся вдоль окружности волновода. Индекс n соответсвует номеру корня функции Бесселя и определяет число стоячих полуволн поля укладывающихся вдоль радиуса волновода.